электростатическое поле является вихревым или потенциальным

Как сказал.

Вопросы к экзамену

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

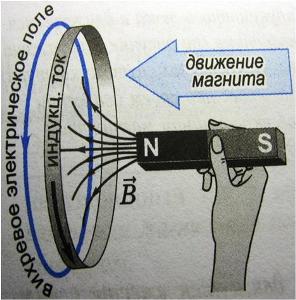
Вихревое электрическое поле

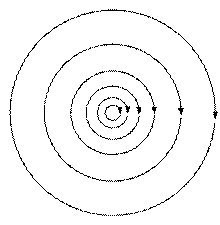
Переменное магнитное поле порождает инду­цированное электрическое поле. Если магнитное поле постоянно, то индуциро­ванного электрического поля не возникнет. Следовательно, индуцированное электрическое поле не связано с зарядами, как это имеет место в случае элект­ростатического поля; его силовые линии не начинаются и не заканчиваются на зарядах, а замкнуты сами на себя, подобно силовым линиям магнитного поля. Это означает, что индуцированное электрическое поле, подобно магнитному, является вихревым.

Если неподвижный проводник поместить в переменное магнитное поле, то в нем индуцируется э. д. с. Электроны приводятся в направленное движение электрическим полем, индуцированным переменным магнитном полем; возни­кает индуцированный электрический ток. В этом случае проводник является лишь индикатором индуцированного электрического поля. Поле приводит в движение свободные электроны в проводнике и тем самым обнаруживает себя. Теперь можно утверждать, что и без проводника это поле существует, обладая запасом энергии.

Сущность явления электромагнитной индукции заключается не столько в появлении индуцированного тока, сколько в возникновении вихревого электрического поля.

Это фундаментальное положение электродинамики установлено Максвел­лом как обобщение закона электромагнитной индукции Фарадея.

В отличие от электростатического поля индуцированное электрическое поле является непотенциальным, так как работа, совершаемая в индуцированном электрическом поле, при перемещении единичного положительного заряда по замкнутому контуру равна э. д. с. индукции, а не нулю.

Направление вектора напряженности вихревого электрического поля уста­навливается в соответствии с законом электромагнитной индукции Фарадея и правилом Ленца. Направление силовых линий вихревого эл. поля совпадает с направлением индукционного тока.

Так как вихревое электрическое поле существует и в отсутствие проводника, то его можно применять для ускорения заряженных частиц до скоростей, со­измеримых со скоростью света. Именно на использовании этого принципа основано действие ускорителей электронов — бетатронов.

Индукционное электрическое поле имеет совершенно другие свойства в отличии от электростатического поля.

Отличие вихревого электрического поля от электростатического

1) Оно не связано с электрическими зарядами;
2) Силовые линии этого поля всегда замкнуты;
3) Работа сил вихревого поля по перемещению зарядов на замкнутой траектории не равна нулю.

Источник

Потенциальность электростатического поля

Потенциальное (консервативное) поле − это поле, в котором работа при перемещении зависит только лишь от конечной и начальной точки пути и не зависит от траектории движения тела.

Что такое потенциальное поле

Есть и другое абсолютно равнозначное определение потенциальности поля (консервативной силы).

Известно, что сила гравитации F G

На основе принципа суперпозиции из потенциальности поля точечного заряда следует потенциальность произвольного электростатического поля.

Легко докажем это математически. Циркуляция вектора напряженности поля точечного заряда E i → по любому замкнутому контуру равняется 0 :

Если поле создает N точечных зарядов, тогда по принципу суперпозиции результирующее поле находим как:

Что такое ротор. Практические задачи

Ротор − это вектор, проекция которого на направление единичного вектора n → определяется таким образом:

Обращаем внимание, что в формуле большой буквой S обозначена площадь, а маленькой буквой s − линейное перемещение.

Ротор описывает интенсивность «завихрения» вектора. На практике при вычислении ротора применяют следующие формулы:

Независимость работы от пути перемещения заряда в электростатическом поле выражается формулой:

где L 1 и L 2 − это различные пути между точками А и В . При замене местами пределов интегрирования получаем:

Выражение ∫ A L 1 B E → · d s → = ∫ A L 2 B E → · d s → представим в виде:

к уравнению выше, получаем:

Это дифференциальная формулировка потенциальности электростатического поля.

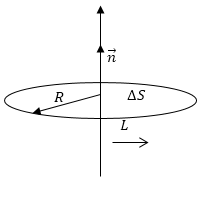
Необходимо найти r o t n υ → для точек оси вращения, если υ → − это вектор скорости точек твердого тела, вращающегося с угловой скоростью ω вокруг оси коллинеарной n →

Решение

В качестве контура L выберем окружность радиусом R с центром на оси вращения, перпендикулярную оси (рисунок 1 ). Известно, что:

где ∮ d s = 2 π R − это длина окружности.

Необходимо доказать, что из условия потенциальности поля следует: тангенциальные составляющие напряженности электростатического поля непрерывны.

Решение

Поскольку электростатическое поле потенциально, тогда выполняется равенство:

Тангенциальные составляющие − это касательные к произвольной поверхности в любой ее точке. Непрерывность значит, что значения касательных составляющих напряженности одинаковы по обеим сторонам поверхности.

Источник

Потенциальный характер электростатического поля

3 ПОТЕНЦИАЛЬНЫЙ ХАРАКТЕР ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

В данном разделе мы будем изучать свойство потенциальности на примере электростатического поля в вакууме, созданного неподвижными электрическими зарядами. Далее мы увидим, что существуют не только потенциальные, но и вихревые электрические поля, например, индукционное электрическое поле. Такое вихревое электрическое поле порождается магнитным полем, изменяющимся с течением времени, в соответствии с законом электромагнитной индукции Фарадея.

Рассмотрим точечную заряженную частицу, находящуюся в вакууме во внешнем электростатическом поле с напряженностью . При перемещении частицы, имеющей заряд q, из точки 1 в точку 2 электростатические силы совершают работу (рисунок 4)

, (3.1)

где — тангенциальная составляющая вектора внешнего электростатического поля относительно элемента траектории .

Поле некоторых сил называется потенциальным, если работа, совершаемая при перемещении тела в этом поле, не зависит от формы траектории и определяется только начальным и конечным положением тела.

Электростатическое поле удовлетворяет этому определению и является потенциальным. Поэтому результат интегрирования в формуле (3.1) не изменяется при выборе любой траектории частицы.

Можно дать также и другое определение потенциального поля: это такое поле, в котором работа, совершаемая при перемещении тела по любому замкнутому контуру, равна нулю.

Математически условие потенциальности можно сформулировать, используя понятие циркуляции вектора по замкнутому контуру :

(3.2)

Соотношение (3.2) называют теоремой о циркуляции вектора , или условием потенциальности электростатического поля в интегральной форме.

Хорошо известным примером потенциального поля является гравитационное поле, которое, как и электростатическое поле, убывает обратно пропорционально квадрату расстояния от тела, создающего поле. Можно доказать, что потенциальность поля точечной заряженной частицы связана с обратной квадратичной зависимостью напряженности поля от расстояния. Далее на основании принципа суперпозиции можно утверждать, что произвольное электростатическое поле также является потенциальным.

Циркуляцию некоторого вектора по замкнутому контуру можно преобразовать с помощью теоремы Стокса

, (3.3)

где — ротор вектора , который можно представить в виде векторного произведения оператора «набла» на вектор ;

— орты декартовой системы координат x, y, z;

– поверхность произвольной формы, границей которой является контур , положительная нормаль к поверхности образует с направлением обхода контура правовинтовую систему.

Для выполнения теоремы Стокса (3.3) необходимо, чтобы на всей поверхности компоненты векторного поля имели непрерывные частные производные по координатам. Мы предполагаем, что реальные физические поля соответствуют этому требованию, и поэтому для них, в том числе и для вектора напряженности электрического поля , теорема Стокса (3.3) является справедливой.

Используя теорему Стокса для вектора , условие потенциальности электростатического поля можно записать в дифференциальной форме:

(3.4)

Из условий (3.3) и (3.4) следует, что поскольку электростатическое поле является потенциальным, то его силовые линии не могут быть замкнутыми. Проведём доказательство от противного и допустим, что существует хотя бы одна замкнутая силовая линия электростатического поля. Выберем эту линию в качестве траектории перемещения точечного заряда. Поскольку для всех элементов такой траектории векторы и совпадают по направлению, то , и из формулы (3.1) следует, что электростатическое поле совершило бы положительную, не равную нулю работу при перемещении заряжённой частицы по замкнутой траектории. Но такой вывод противоречил бы условию потенциальности электростатического поля (3.2).

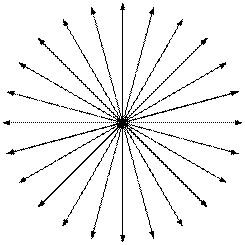
В качестве примера можно рассмотреть самые простые и часто встречающиеся электрические поля: точечного заряда, пары точечных зарядов, нити, цилиндра, сферы, шара, плоскости, плоского слоя. Во всех указанных случаях силовые линии электростатического поля начинаются на положительных зарядах и заканчиваются на отрицательных зарядах, либо уходят в бесконечность, в электростатическом поле замкнутых линий вектора не существует.

Кроме напряженности , электрическое поле характеризуется также скалярным потенциалом . Чтобы ввести в рассмотрение скалярный потенциал электростатического поля, можно воспользоваться соотношением, известным из векторного анализа: . Это соотношение является тождественным равенством, то есть выполняется для любой функции . Сравнивая данное соотношение и формулу (3.4), приходим к выводу, что напряжённость электростатического поля можно представить в виде градиента некоторой функции , которая и называется скалярным потенциалом:

, (3.5)

где — градиент скалярной функции j .

Как следует из определения градиента, он является вектором, и это свойство отражено в соотношении (3.5). Единицей измерения потенциала является вольт [В].

В разделе 9 будет показано, что потенциал электростатического поля равен отношению потенциальной энергии заряда, находящегося в данной точке поля, к величине заряда.

Соотношение (3.5) показывает, что напряженность электростатического поля направлена в сторону самого быстрого убывания потенциала в пространстве. Модуль напряженности равен скорости изменения потенциала в направлении, задаваемом градиентом. Напряженность направлена перпендикулярно эквипотенциальной поверхности, то есть такой поверхности, во всех точках которой потенциал имеет одинаковые значения.

В отличие от напряженности, потенциал является неоднозначной функцией и определен с точностью до произвольной постоянной. Чтобы избежать неоднозначности, при решении конкретной задачи производят нормировку потенциала, т. е. приписывают ему определенное значение в некоторой точке. Например, можно считать потенциал равным нулю на поверхности Земли, если рассматривается электрическое поле вблизи земной поверхности. Если заряженные частицы расположены в некоторой ограниченной области, а электрическое поле рассматривается во всем пространстве, то обычно используется другое условие нормировки:

(3.6)

Физический смысл имеет не сам потенциал, а разность потенциалов в двух точках поля. Она численно равна работе, совершаемой полем при перемещении частицы с единичным положительным зарядом из первой точки во вторую:

(3.7)

где учтено соотношение (3.5).

Электростатическое поле является потенциальным, поэтому работа при перемещении частицы в поле не зависит от выбора траектории пробной частицы. Это свойство поля проявляется в формуле (3.7), согласно которой разность потенциалов определяется положением двух точек поля.

В электростатике разность потенциалов двух точек поля называют также электрическим напряжением между этими точками. Разность потенциалов и напряжение, так же как и потенциал, измеряются в вольтах. Из соотношения (3.7) следует, что 1В = 1Дж/1Кл.

Важным идеальным примером электростатического поля является однородное поле, напряженность которого не зависит от координат, то есть не изменяется в пространстве в пределах некоторой области. Силовые линии однородного электростатического поля представляют собой параллельные прямые. Густота силовых линий постоянна в пределах той области, в которой выполняется условие однородности поля. Для напряженности однородного электростатического поля из соотношения (3.7) можно получить формулу

, (3.8)

где — разность потенциалов между двумя точками пространства, лежащими на одной силовой линии;

– расстояние между этими точками.

Согласно (3.8), напряженность электрического поля может быть измерена в единицах В/м. Ранее на основании формулы (1.5) мы получили, что единицей измерения напряжённости является Н/Кл.

С некоторыми допущениями можно считать, что однородное поле существует внутри плоского конденсатора вдали от краев его обкладок. Конденсатором называется система, состоящая из двух проводников, имеющих одинаковые по величине, но противоположные по знаку заряды. Эти проводники называются обкладками конденсатора. Если обкладки имеют форму плоскостей, то конденсатор называется плоским. Обычно в конденсаторе расстояние между обкладками значительно уступает по величине линейным размерам обкладок, и этим обеспечивается однородность электростатического поля внутри конденсатора. В случае плоского конденсатора также можно применить формулу (3.8), при этом — электрическое напряжение на конденсаторе, – расстояние между его обкладками.

Потенциал поля точечной частицы с зарядом при условии нормировки (3.6) равен

, (3.9)

Для скалярного потенциала, так же как и для напряженности электрического поля, применим принцип суперпозиции:

. (3.10)

Согласно (3.10), потенциал электрического поля, создаваемого несколькими заряжёнными частицами в любой точке пространства, равен сумме потенциалов полей всех зарядов, причем потенциал каждого поля вычисляется при условии отсутствия всех других полей.

Используя принцип суперпозиции (3.10), можно вычислить потенциал системы точечных частиц с зарядами , расположенных в точках с координатами :

, (3.11)

где — координаты точки пространства, в которой определяется потенциал.

При непрерывном распределении заряда в некоторой области выражение для потенциала имеет вид

, (3.12)

где — объемная плотность заряда;

В заключение данного раздела произведем формальное сравнение математических величин, введенных в рассмотрение в векторном анализе и широко используемых в электромагнетизме:

а) дивергенция вектора – вычисляется в результате дифференцирования векторного поля по пространственным координатам, является скалярной величиной, связана с потоком вектора через замкнутую поверхность и характеризует расходимость линий вектора в пространстве, то есть наличие источников линий вектора в данной точке пространства;

б) ротор вектора – вычисляется в результате дифференцирования векторного поля по пространственным координатам, является векторной величиной, связан с циркуляцией исходного вектора по замкнутому контуру и ассоциируется с замкнутостью линий исходного вектора в пространстве вблизи данной точки;

Источник

Потенциальное и вихревое поле

Различают два основных типа векторных полей: потенциальные (безвихревые) и вихревые (соленоидальные) поля. Физические свойства их различны.

Потенциальное поле тесно связано со своим источником, линии поля имеют начало (исток) и конец (сток). Линии вихревого поля всегда непрерывны и не имеют источников (рисунок 12).

Рисунок 12 − Потенциальное и вихревое поля

Для потенциального поля имеем

,

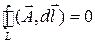
то есть циркуляция вектора по любому замкнутому контуру равна нулю.

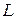
Если поле является вихревым, то поток вектора через любую замкнутую поверхность равен нулю:

.

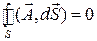
В дальнейшем будет показано, что электростатическое поле является только потенциальным, магнитное – вихревым.

Дата добавления: 2015-10-19 ; просмотров: 5416 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Учебники

Журнал «Квант»

Общие

Вихревое электрическое поле

Если замкнутый проводник, находящийся в магнитном поле, неподвижен, то объяснить возникновение ЭДС индукции действием силы Лоренца нельзя, так как она действует только на движущиеся заряды.

Известно, что движение зарядов может происходить также под действием электрического поля Следовательно, можно предположить, что электроны в неподвижном проводнике приводятся в движение электрическим полем, и это поле непосредственно порождается переменным магнитным полем. К этому выводу впервые пришел Дж. Максвелл.

Электрическое поле, создаваемое переменным магнитным полем, называется индуцированным электрическим полем. Оно создается в любой точке пространства, где имеется переменное магнитное поле, независимо от того, имеется ли там проводящий контур или нет. Контур позволяет лишь обнаружить возникающее электрическое поле. Тем самым Дж. Максвелл обобщил представления М. Фарадея о явлении электромагнитной индукции, показав, что именно в возникновении индуцированного электрического поля, вызванного изменением магнитного поля, состоит физический смысл явления электромагнитной индукции.

Индуцированное электрическое поле отличается от известных электростатического и стационарного электрического полей.

1. Оно вызвано не каким-то распределением зарядов, а переменным магнитным полем.

2. В отличие от линий напряженности электростатического и стационарного электрического полей, которые начинаются на положительных зарядах и заканчиваются на отрицательных зарядах, линии напряженности индуцированного поля — замкнутые линии. Поэтому это поле — вихревое поле.

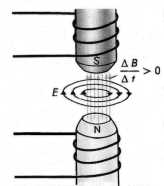
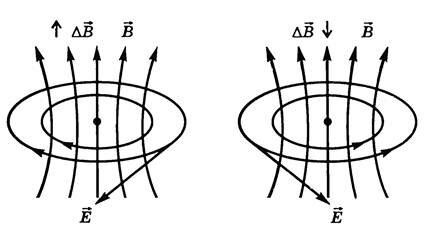
Исследования показали, что линии индукции магнитного поля и линии напряженности вихревого электрического поля расположены во взаимно перпендикулярных плоскостях. Вихревое электрическое поле связано с наводящим его переменным магнитным полем правилом левого винта:

если острие левого винта поступательно движется по направлению ΔΒ, то поворот головки винта укажет направление линий напряженности индуцированного электрического поля (рис. 1).

3. Индуцированное электрическое поле не является потенциальным. Разность потенциалов между любыми двумя точками проводника, по которому проходит индукционный ток, равна 0. Работа, совершаемая этим полем при перемещении заряда по замкнутой траектории, не равна нулю. ЭДС индукции и есть работа индуцированного электрического поля по перемещению единичного заряда по рассматриваемому замкнутому контуру, т.е. не потенциал, а ЭДС индукции является энергетической характеристикой индуцированного поля.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 350-351.

Источник