формула золотого сечения в строительстве крыши
Какой должна быть высота крыши дома
Высота крыши влияет как на эстетику дома, так и на чисто практические параметры. Включая, например, количество снега, которое будет задерживаться на скатах зимой, или полезную площадь мансардного этажа. Даже возможность смонтировать на кровле конкретное кровельное покрытие и то зависит от крутизны скатов.
Иными словами, решать, какой высоты должна быть крыша, по принципу «нравится или нет» нельзя. Нужно учесть много тонкостей, чтобы крыша, да и весь дом в целом, получились и красивыми, и практичными. Для упрощения этой задачи предлагаем разбить ее на три этапа.
Содержание
Этап №1: Минимальная и максимальная высота кровли по уклону
Подбор уклона кровли — один из важнейших этапов расчета стропильной системы. Но как он связан с расчетом высоты крыши?
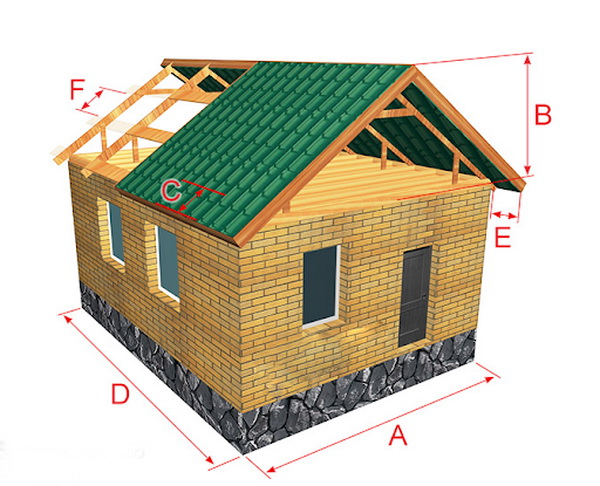
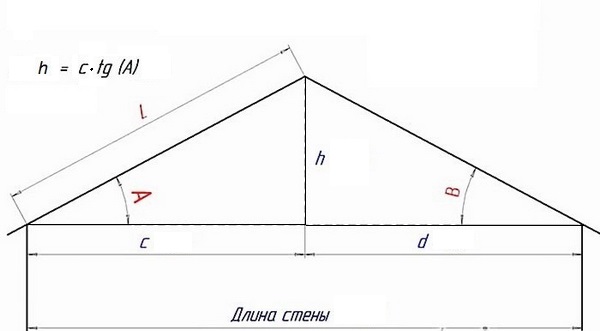
Все просто: любую крышу можно представить как набор прямоугольных треугольников. В частности, для симметричной двускатной кровли скат — это гипотенуза, высота — один катет, а половина ширины дома — второй катет. Следовательно, при увеличении или уменьшении угла наклона ската меняется и высота крыши.
Поэтому, чтобы рассчитать высоту крыши по известному уклону используют формулу:
Здесь h — это высота кровли, c — расстояние между краем карнизного свеса и коньком, A — угол наклона ската.
Тангенс рассчитывают на калькуляторе или смотрят по таблицам Брадиса. Значения тангенса для некоторых углов приведены в таблице:
| Угол наклона А, градусы | 20 | 22 | 24 | 25 | 26 | 28 | 30 | 32 |
| tg(A) | 0.364 | 0.404 | 0.445 | 0.466 | 0.488 | 0.532 | 0.577 | 0.625 |
| Угол наклона А, градусы | 34 | 35 | 36 | 38 | 40 | 42 | 44 | 45 |
| tg(A) | 0.674 | 0.7 | 0.726 | 0.781 | 0.839 | 0.9 | 0.966 | 1 |
| Угол наклона А, градусы | 46 | 48 | 50 | 52 | 54 | 55 | 56 | 58 |
| tg(A) | 1.035 | 1.111 | 1.192 | 1.28 | 1.376 | 1.428 | 1.482 | 1.6 |
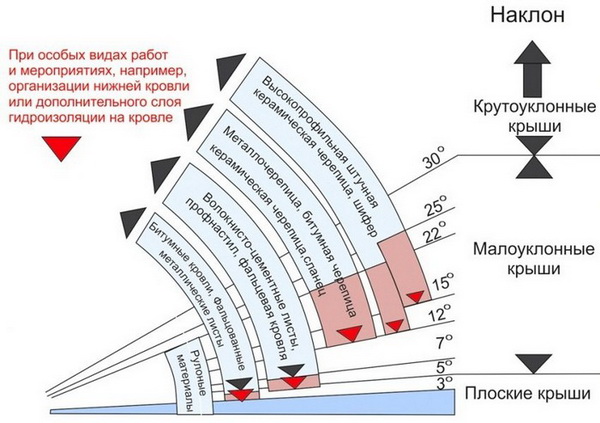
Из-за прямой зависимости от уклона кровли, перед тем как рассчитать высоту крыши дома, нужно сначала вычислить минимальные и максимальные углы наклона скатов. Они зависят от:
Уклон кровли в зависимости от кровельного материала
С кровельным покрытием проще всего: у всех материалов, кроме тех, что предназначены для монтажа на плоскую крышу, есть ограничение по минимальному углу наклона ската. У некоторых есть такое ограничение и по максимальному уклону. В частности, керамическую и цементно-песчаную черепицу нельзя монтировать на участки кровли, уклон которых больше 60°, а шифер недопустимо укладывать при угле наклона крыши 45° и более.
Если уклон ската меньше минимального для выбранного вида материала, то это не значит, что его в принципе нельзя использовать в качестве кровельного покрытия. Но затраты на устройство кровли сильно вырастут, поскольку под кровельным покрытием нужно будет сделать герметичный гидроизолирующий слой из специальной мембраны или полимерно-битумных материалов.
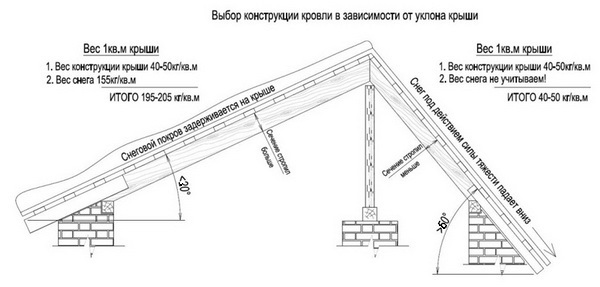
Влияние снеговой нагрузки на уклон и высоту кровли
После выбора кровельного материала нужно учесть снеговую нагрузку. В отличие от веса самого кровельного пирога, масса снеговой шапки на крыше сильно зависит от угла наклона скатов. Так, согласно нормативу СП 20.13330.2016 «Нагрузки и воздействия» для простой односкатной или двускатной крыши:
То есть, меняя уклон в диапазоне от 30° до 60°, мы меняем и расчетную нагрузку на стропильную систему. Это позволяет рассчитать минимально допустимый угол наклона и высоту кровли в зависимости от несущей способности стропильной системы.
Это упрощенный пример, подробнее о расчете снеговой нагрузки и уклона кровли читайте здесь.
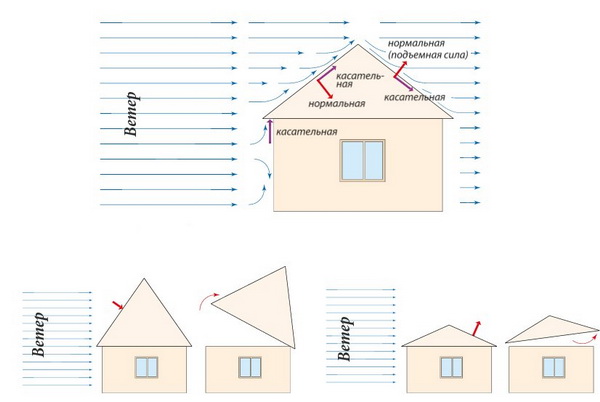
Учитываем ветровое давление
Если снеговую нагрузку большая высота крыши относительно высоты дома и, соответственно, крутые скаты снижают до нуля, то с ветровой нагрузкой все с точностью до наоборот.
С наибольшей силой ветер «давит» на вертикальные препятствия: сплошные заборы, стены зданий, рекламные щиты. С наименьшей — на горизонтальные поверхности. Следовательно, чем более пологая крыша, тем меньше прямое давление ветра на скаты. Но здесь важен баланс, поскольку при обтекании кровли воздушными массами на ее подветренной стороне создается подъемная сила. И она увеличивается с уменьшением высоты кровли.
Поэтому с точки зрения ветровой нагрузки оптимальным углом наклона крыши считается диапазон от 30° до 45°.
Этап №2: какой высоты должна быть крыша относительно дома
На первом этапе расчетов мы получили допустимые значения уклона и, соответственно, высоты крыши. Например, если ширина дома 10 м, а угол наклона скатов должен быть равен 25-45°, высота кровли должна быть в диапазоне от 2,33 м до 5 м. Что делать дальше? Рекомендуем воспользоваться правилом золотого сечения.
Золотое сечение — это официально самая красивая пропорция в мире, которая равна 62/38 или, если точнее, 1,618. Эта пропорция повсеместно встречается в природе, ее использовали знаменитые художники и, что важнее в нашем случае, архитекторы для создания своих шедевров.
Как использовать принцип золотого сечения в частном строительстве? Все просто: соотношение высоты крыши к высоте дома должно быть равно 38% и 62% соответственно. В этом случае кровля будет смотреться пропорционально, а не нависать над домом. Идеально точно выдержать такие пропорции крыши по отношению к дому, но допустимы и небольшие расхождения.
Приведем пример. Допустим, у нас есть здание, высота этажа у которого равна 3 м. Еще примерно 0,5 м приходится на цоколь. Какая высота крыши по отношению к дому должна быть в этом случае? Сложив высоту цоколя и этажа, получаем 3,5 м — это 62%. Следовательно, 38% — это примерно 2,15 м. Для удобства расчетов высоту дома можно просто разделить на 1,618.
Из этого примера видно, что чем выше дом, тем выше должна быть кровля. Так, если высота крыши одноэтажного дома по принципу золотого сечения редко превышает 3 м, то для двухэтажного здания она уже обычно более 4 м, а для трехэтажного приближается к 6 м. То есть на многоэтажных домах хорошо смотрятся крутые кровли, а на одноэтажных — относительно пологие.
Этап №3: высота крыши дома, оптимальная для мансарды
Во время последнего этапа разбираемся, как высота крыши относительно высоты дома зависит от назначения подкровельного пространства: нормы для чердака и для мансарды сильно отличаются.
Если под кровлей будет чердак, то ее высота особого значения не имеет. Даже под очень пологими скатами место для хранения вещей будет.
Другое дело, если планируется мансарда. В этом случае высота кровли прямо влияет на полезную площадь подкровельного жилого пространства. Причем по-разному, в зависимости от вида кровли:
При этом учитывайте, что по высоте крыша все равно должна вписываться в пропорции золотого сечения и диапазон, заданный вычислениями максимально и минимального уклона.
Подведем итоги
Какая высота крыши должна быть:
Как правильно рассчитать высоту крыши:
Кроме того, при выборе высоты крыши нужно учитывать, что планируется в подкровельном пространстве: мансарда или чердак.
Правило золотого сечения в архитектуре, строительстве и дизайне
Наблюдения за природой и попытки раскрыть тайны ее прекрасных созданий принесли немало открытый. Одно из них — золотое сечение. Это некоторая закономерность, которой подчиняется все, что мы называем красивым. Люди, животные, цветы, здания, галактики…
Что такое золотое сечение и как его понимать
Часто мы сталкиваемся с домами, предметами, строениями, растениями, которые нас чем-то завораживают. Люди издавна пытались понять, почему одно нам кажется красивым, другое нет, искали закономерности. И вроде нашли. Это некоторое соотношение частей, которое назвали золотым сечением.
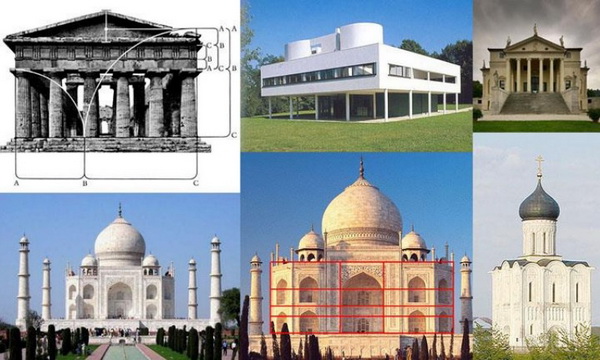
О том, кто и когда придумал золотое сечение никто не знает точно. Кто-то приписывает открытие Пифагору, но первое упоминание нашли еще в «Началах» Евклида, а жил он в 3 веке до нашей эры. Так что находка явно давняя. Именно по этому принципу построены древнегреческие и римские храмы. Конечно, это могут быть совпадения, но очень уж странные и очень их много. Так что, скорее всего, они были в курсе идеальных пропорций.

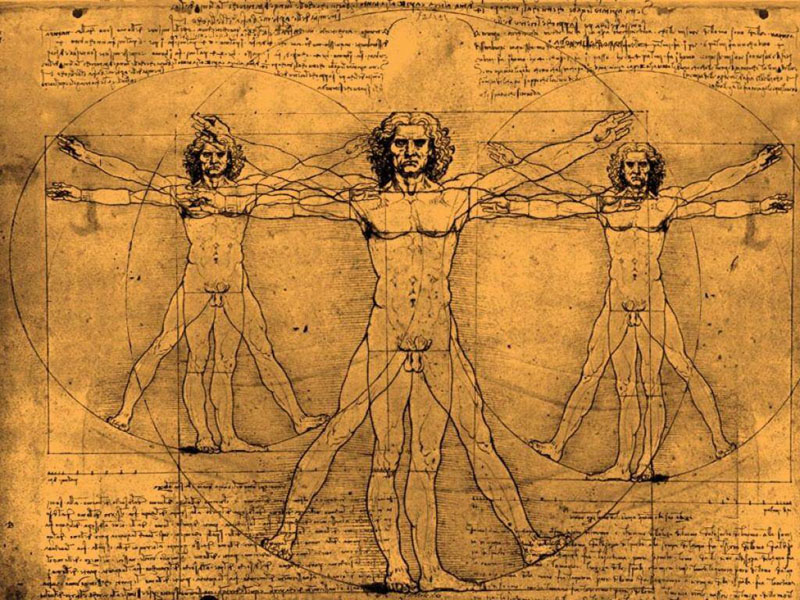
Совершенно точно то, что Леонардо да Винчи искал подтверждение этому принципу в строении человеческого тела. И, что самое интересное, нашел. Те лица и тела, которые кажутся нам красивыми, имеют пропорции, которые как раз и подчиняются закону золотого сечения.
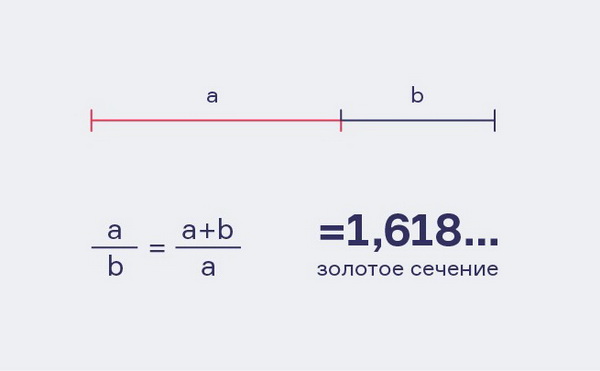
Формальное определение звучит и просто, и сложно. Его связывают с двумя разными по размеру отрезками. Звучит этот принцип примерно так: если отрезок разделить на две неравные части, то это деление будет пропорциональным, если большая часть отрезка относится к целому так же, как и меньшая часть к большему. Будет понятнее, если посмотреть на иллюстрацию и формулу.

На рисунке целый отрезок разделен так, что если а разделить на b, получим 1,1618, та же цифра получается, если целый отрезок разделить на большую часть — a. Это число и есть воплощением идеальной пропорции. Теперь, если посмотрите на картинку с Парфеноном, пропорции этого строения также подчиняются указанному соотношению.
Ту же закономерность можно представить в виде процентов. Может, кому-то так проще. Для того, чтобы деление целого было пропорциональным, части должны составлять 62% и 38%. Возможно, так будет проще запомнить.
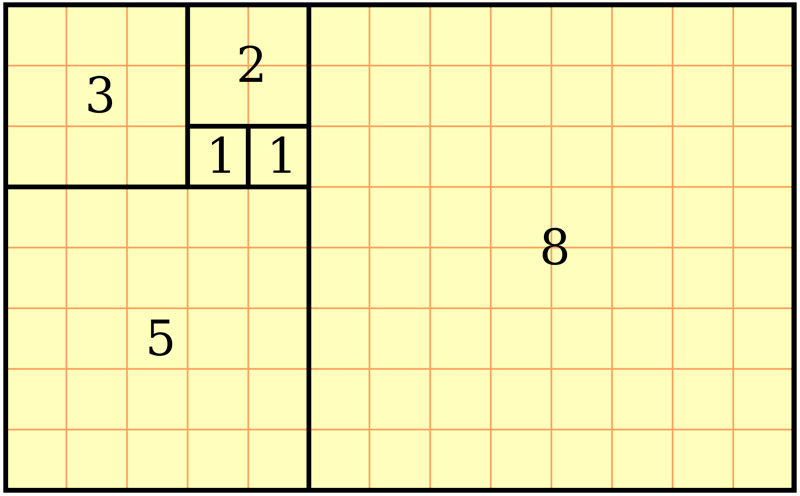
Эту закономерность развил дальше математик Фибоначчи. Он разработал числовую последовательность, элементы которой, начиная с девятого, подчиняются тому же закону. Графическое изображение этой последовательности — спираль. Если присмотреться, и в природе, и в архитектуре, и в человеческом теле пропорции красоты присутствуют.
Как построить прямоугольник с идеальными пропорциями
Чтобы применять на практике полученную информацию, надо каким-то образом научиться делить пространство или строить его согласно этому закону. Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.

Квадрат делим пополам, в одном из полученных прямоугольников проводим линию, которая соединяет противоположные углы. Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).

Что еще интересно, что если вы начнете делить прямоугольник с соотношением сторон 1,62 на квадрат и прямоугольник, вы получите снова прямоугольник с идеальными пропорциями, но меньшего размера. Если вы его снова разделите по тому же принципу, будет еще одна пара квадрат+прямоугольник со сторонами, соотношение которых будет соответствовать золотому сечению. И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.
Как разделить отрезок по правилу золотого сечения
Это умение пригодится, например, при создании проекта дома, планировки, при разработке дизайна квартиры, расстановке мебели и т.д. Точно также может понадобиться при планировке участка, клумб, высадке растений и т.д. В общем, применяться может практически везде.

Итак, порядок деления отрезка по правилу золотого сечения:
Пару раз повторив процедуру, вы научитесь делать все буквально за считанные минуты. Если же вам надо, например, определить высоту окна, его форму, также можно воспользоваться данными пропорциями. По тому же принципу можно определять местоположение всех архитектурных элементов, их размеры. При планировании уже имеющихся объектов, деление проще проводить при помощи процентного соотношения. Тут уже либо считаете в уме, либо используете калькулятор.
Идеальный треугольник и пентаграмма
Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.

Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.
Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.
Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.
Применение в строительстве
Как уже говорили, неизвестно кто открыл золотое сечение, но все, что кажется нам красивым, имеет именно такое соотношение сторон. Примеров в природе очень много. Если рассматривать известные здания, то и там тоже есть та же закономерность.

Если вы хотите, чтобы ваш дом внутри и снаружи был привлекательным, запоминался и нравился, при создании или выборе проекта можно просчитать хотя бы основные пропорции. Внести корректировки в пропорции, возможно, не всегда легко, часто связано с дополнительными расходами. Но, если при создании проекта сразу держать в уме золотое сечение, вопросы сами по себе отпадают. На самом деле не так уж это сложно.
Например, вы хотите дом площадью около 100 квадратных метров. Длинную сторону можно принять за 12 метров. Тогда короткая находится как 62% от длинной и составит 7,44 метра. Можно сделать 7 метров или 7,5, можно увеличить до 8. Точное, до сантиметра соблюдение размеров совсем не обязательно. Важно соотношение. А «на глаз» даже в приближении смотрится гармонично. Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов. Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.

Высота этажа в таком случае принимается как 32% от длинной части. Она составит 12*0,32 = 3,84 метра. В принципе, это соответствует нынешним представлениям о комфортных габаритах помещения, но при желании можно сделать высоту меньше. Примерно также рассчитываются, подбираются все остальные фрагменты дома.
Не стоит забывать, что дом должен вписываться также в ландшафт. Если есть какая-то доминанта — высокий холм, например, то просчитывать надо и соотношение с холмом, и с пропорциями участка. В общем, для создания гармоничной усадьбы очень многие факторы надо учитывать.

По такому же принципу разрабатывают внутреннюю планировку, стараясь по возможности соблюдать требуемое соотношение. Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.
Золотое соотношение во внутреннем оформлении
Что еще дает золотое сечение кроме визуального наслаждения? Психологи говорят, что в интерьере, созданном по этому правилу человек чувствует себя более комфортно. Это, конечно, субъективно, но можно попробовать. Итак, вот как интерпретируют правило золотого сечения в дизайне интерьеров:
Относительно мебели правило кажется непонятным, но это только на первый взгляд. Например, подбираем группу отдыха. Крупный предмет в этом случае — диван или софа. Средний — журнальный или кофейный столик, кресла. Мелкие — аксессуары. Так вот, размеры журнального столика не должны быть больше длинной стороны дивана, кресла — не больше его короткой стороны. Аксессуары по размерам не больше размеров столика или кресел. В идеале, они соотносятся с ними как 62% и 38%.

Почему не указывается точное соотношение? Потому что, во-первых, найти такие предметы нереально. Во-вторых, золотое сечение — это не только 62% и 38%. Это еще и последовательность Фибоначчи, следование которой также делает оформление гармоничным. Есть люди, у которых следование этой последовательности является «встроенной функцией». Им не надо считать, они выбирают основываясь на чутье и интуиции. Но если проанализировать их выбор, пропорции будут близки к идеальным. Вот так.
Золотое сечение в ландшафтном дизайне
При создании ландшафта на участке, принцип идеальных пропорций применяют, называя его правилом треугольника. В композиции должна быть одна доминанта, остальные ее составляющие лишь подчеркивают, оттеняют ее. Например, на участке есть большое дерево и вы хотите его обыграть. Оно и будет центром композиции — доминантой. Нанесите его на план, расчертите клумбу или рокарий, альпинарий — то, что хотите сделать.

От главенствующего растения или камня, под прямым углом проведите две линии. На этих линиях надо будет высадить более низкие растения. Причем второе по высоте не должно быть выше чем 2/3 от высоты основного объекта. Третий объект — не выше чем 1/3. Дополняют композицию еще более низкорослыми насаждениями. Это коротко о том, как применять золотое сечение в планировке посадок.
Но это не все. Растения надо подбирать по цветам — сочетание зелени разных оттенков, вкрапления цветов и декоративно-лиственных растений — все подчиняется тому же закону. Доминирующий оттенок составляет порядка 60%, дополнительные цвета — 30%, акценты — 10 %. Это если говорить о правилах подбора в одной группе. Но также надо согласовывать и весь план целиком — по размерам, высоте, цветам.
Тайны ряда Фибоначчи: как работает принцип золотого сечения в архитектуре
Почему нас так привлекают строения древней архитектуры, при виде которых мы испытываем гармонию и умиротворение? Все они были построены на основе золотого сечения, данная зависимость прослеживается и в средневековье, и в современном мире. Математическая пропорция встречается повсеместно: это и ракушки моллюсков, и знаменитые картины художников, и строение человеческого тела, и даже египетские пирамиды. Сегодня об обзоре редакции Homius.ru расскажем простыми словами, как и, самое главное, зачем нужно использовать божественную гармонию чисел, и как она поможет в строительстве собственного дома и оформлении интерьера.
Просто о сложном: что это такое – правило золотого сечения
Золотое сечение –это правило общей пропорции, которая создает универсальную композицию. Математики называют её формулой божественной гармонии или асимметричной симметрией.
Это интересно! Общее определение правила ЗС –меньшая величина относится к большей, как большая к целому. Было рассчитано приблизительное число, равное 1,6180339887, это и есть коэффициент золотого сечения. Если смотреть в процентном соотношении, то в одном целом меньшая величина занимает 38%, большая – 62%.
Признано считать, что ЗС пришло к нам еще с древней Греции, но есть и такое мнение, что его греки подсмотрели у египтян. Если проанализировать архитектуру Египта того времени, можно чётко проследить соблюдение математической гармонии. Необычные свойства числовой зависимости стали причиной мистического отношения к золотому сечению:
Экскурс в историю: кто придумал золотое сечение
Представление о золотой пропорции имели и древние греки, и египтяне, известно было о ней и на Руси. Но впервые ещё в 1509 году в книге «Божественная Пропорция», иллюстрации к которой принадлежат Леонардо да Винчи, монах Лука Пачоли дал научное определение правилу. Он видел в золотом сечении божественное единство:
Это интересно! Историки присваивают Леонардо да Винчи определение термина ЗС, поскольку он долгое время изучал божественную закономерность и воплощал её принцип в своих творениях.
Вторую жизнь ЗС получило в 1855 году благодаря философу Адольфу Цейзингу. Он доработал теорию до абсолютного идеала, и она стала универсальной для всех проявлений. Все это он описал в своей книге «Математическое Эстетство», на которое в свое время обрушилось много негатива и критики.
Золотое сечение в божественной пропорции
Принцип расчета и построения золотого сечения
Примеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений, только нужно знать, как правильно его увидеть. Для этого достаточно посмотреть на строение всего 5 минут.
Как определить число золотого сечения
С пропорцией ЗС связывают астронома из Италии Фибоначчи, он вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Сегодня эта закономерность известна как ряд Фибоначчи:
Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленные значения 0,62 и 0,38.
Ряд Фибоначчи в церкви Покрова на Нерли
Как рассчитать золотое сечение на простейшем примере
Проще всего объяснить гармонию ЗС можно на примере обычного куриного яйца, точнее на удалении всех точек скорлупы от центра тяжести. Именно форма оболочки, а не её прочность, обеспечила выживаемость птиц столь долгое время и в любых условиях.
Если взять обычный отрезок, который состоит из нескольких маленьких, их длины относятся к большей величине как 0,62. Это показывает, как можно разбить целую линию для получения идеальной пропорции.
Простой пример золотого сечения в курином яйце
Как построить золотое сечение на примере прямоугольника и спирали
Если построить золотой прямоугольник, используя ряд Фибоначчи, он будет выглядеть как единое целое. Рассмотрим зависимость на примере:
Построение золотой спирали из прямоугольника
На видео можно более подробно узнать про магию чисел Фибоначчи: