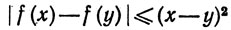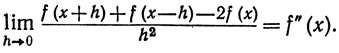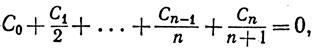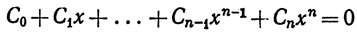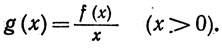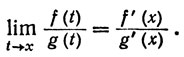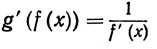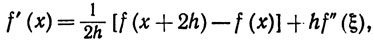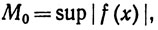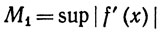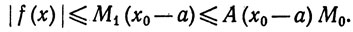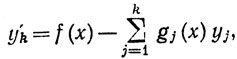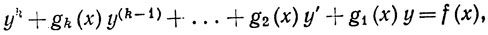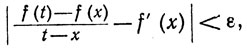Пусть f x x2 2 докажите что

Пусть f x x2 2 докажите что

Пусть функция `y=f(x)` определена на некотором интервале, содержащем точку `ain R`, за исключением, быть может, самой точки `a`.

Число `A` называется пределом функции `y=f(x)` в точке `a`, если для любой последовательности `(x_n)` из области её определения такой, что `x_n!=a` и `lim_(n->oo)x_n=a` выполняется равенство `lim_(n->oo)f(x_n)=A`.

Обозначение: `lim_(n->oo)f(x)=A`, или `f(x)->A` при `x->a`.

В определении предела рассматриваются значения `x_n`, не равные `a`, поэтому в самой точке `a` функция `y=f(x)` может быть не определена; если значение `f(a)` определено, то оно не обязано совпадать с `A`. К тому же, поскольку последовательность `(f(x_n))` имеет не более одного предела, получаем, что если функция `y=f(x)` имеет предел при `x->a`, то этот предел единственный.

На рис. 2 изображена лишь одна последовательность `(x_n)`, которая к тому же является монотонной. Важно понимать, что `lim_(n->oo)f(x_n)=A` для любой последовательности `(x_n)` с условием `x_n!=a` и `lim_(n->oo)x_n=a`.

Доказать, что `lim_(n->oo)x=a`.

Очевидно, функция `f(x)=x` определена на любом интервале, содержащем `a`. Выберем произвольную последовательность `(x_n)` такую, что `x_n!=a` и `lim_(n->oo)x_n=a`. Тогда `f(x_n)=x_n` и, значит, `lim_(n->oo)f(x_n)=a`.

Доказать, что при `a>0lim_(n->a)sqrtx=sqrta`.

Функция `f(x)=sqrtx` определена при `x>=0` и, следовательно, определена на некотором интервале, содержащем `a`. Выберем произвольную последовательность неотрицательных чисел `x_n!=a`, что `lim_(n->oo)x_n=a`. Нам нужно показать, что `lim_(n->oo)sqrtx_n=sqrta`. Фиксируем произвольное `epsilon>0`, тогда найдётся такое число `k`, что при `n>k` выполняется неравенство `|x_n-a| 1)(x^2-1)/(x-1)=2`.

Функция `f(x)=(x^2-1)/(x-1)` определена на любом интервале, содержащем `x=1`, кроме этой точки. Поскольку при `x!=1` имеет место равенство `f(x)=x+1`, то для любой последовательности `(x_n)` такой, что `x_n!=1` и `lim_(n->oo)x_n=1` выполняется `lim_(n->oo)f(x_n)=lim_(n->oo)x_n+1=2`.

Пусть функции `y=f(x)`, `y=g(x)` определены на некотором интервале, содержащем точку `a in R`, за исключением, быть может, самой точки `a`, `lim_(x->a)f(x)=A` и `lim_(x->a)g(x)=B`. Тогда

3) если дополнительно `g(x)!=0` при `x!=a`, `B!=0`, то `lim_(x->a)(f(x))/(g(x))=A/B`.

Эти свойства вытекают из арифметических операций над пределами последовательностей (теорема 2.2). Приведём доказательство для свойства 2. Остальные доказываются аналогично.

Пусть некоторая произвольная последовательность `(x_n)` из интервала, на котором определены функции, такова что `x_n!=a` и `lim_(n->oo)x_n=a`. Тогда по определению предела функции `lim_(n->oo)f(x_n)=A` и `lim_(n->oo)g(x_n)=B`. По пункту 2 теоремы 2.2 `lim_(n->oo)f(x_n)g(x_n)=AB`. По определению предела функции получаем, что `lim_(x->a)f(x)g(x)=AB`.

Пусть функция `y=f(x)` определена на некотором интервале, содержащем точку `a`. Функция `y=f(x)`называется непрерывной в точке `a`, если `lim_(x->a)f(x)=f(a)`, т. е. если для любой последовательности `(x_n)` из области определения функции такой, что `lim_(n->oo)x_n=a`, выполняется равенство `lim_(n->oo)f(x_n)=f(a)`.

Отметим два обстоятельства, связанных с определением непрерывности. Во-первых, оговорка `x_n!=a` здесь не нужна, т. к. при `x_n=a` значения `f(x_n)` равны `f(a)`. Во-вторых, важно понимать, что если функция `y=f(x)` непрерывна в точке `a`, то

1) она определена в точке `a`;

2) существует `lim_(x->a)f(x)=A` и

Если хотя бы один из пунктов 1) – 3) не выполнен, то функция не является непрерывной в точке `a`.

Многочлен является непрерывной на всей числовой прямой функцией.

Из теоремы 3.1 вытекает, что если функции `y=f(x)`, `y=g(x)` непрерывны в точке `a`, то функции `y=f(x)+-g(x)`, `y=f(x)g(x)`, `y=f(x)//g(x)` `(g(a)!=0)` также непрерывны в `a`.

Функция называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.

Функция `y=|x|` непрерывна на всей числовой прямой.

Вообще, все элементарные функции, изучаемые в школьном курсе, непрерывны в каждой точке, в окрестности которой эти функции определены.

Источник

Пусть f x x2 2 докажите что

По многочисленным)) просьбам участников группы задаю ещё одну задачку: доказать, что неубывающее отображение отрезка в себя имеет неподвижную точку (другими словами: для всякой неубывающей функции
f:[0,1] —> [0,1]
существует такое число x из [0,1], что f(x)=x).

Комментарий: эту задачку можно решить совсем просто средствами стандартного матанализа 1-го семестра. Но у неё же есть (на мой взгляд, очень красивое!) решение, использующее трансфинитную индукцию. За решение «первого типа» обещаю студенту 5 баллов по дискретной математике (или алгебре в случае первокурсника), за решение с трансфинитной индукцией — 10.

Здравствуйте, Андрей Юрьевич,

Здравствуйте, Занг! Конечно, существует немонотонная функция, имеющая неподвижную точку!! Конечно же, ВСЯКАЯ _непрерывная_ функция из отрезка в себя имеет неподвижную точку (это так называемая теорема Брауэра, которую для отрезка легко доказать ссылкой на теорему Больцано-Коши).

Но НАША задача не в этом. Наша задача в том, чтобы доказать, что для существования неподвижной точки ДОСТАТОЧНО (но, конечно, не необходимо), чтобы функция была неубывающей. При этом, она, конечно, может не быть непрерывной (иначе задачка становится совсем не интересной).

Итак, надо доказать, что всякая неубывающая функция из отрезка в себя обязательно имеет неподвижную точку. (А обратное утверждение, конечно, неверно, тут Вы правы :-))

Источник

Пусть f x x2 2 докажите что

Упражнения

1. Пусть 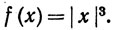Вычислить f'(х), f'(x) при всех вещественных х и показать, что f (3) (0) не существует.

2. Пусть f определена при всех вещественных х, и пусть

при всех вещественных х и у. Доказать, что f постоянна.

3. Пусть f определена в окрестности точки x, и пусть существует f»(x). Показать, что

Показать на примере, что этот предел может существовать и тогда, когда f»(х) не существует.

имеет хотя бы один вещественный корень между 0 и 1.

(a) f непрерывна при x≥0,

(b) f (х) существует при всех x>0,

(d) f монотонно возрастает.

Доказать, что g монотонно возрастает.

7. Пусть f'(x), g'(х) существуют, g'(х)≠ и f(х) = g(х) = 0. Доказать, что

(это верно и для комплексных функций.)

11. Сформулировать и доказать неравенство, которое следует из теоремы Тейлора и остается верным для векторнозначных функций.

Указание. Из теоремы Тейлора следует, что

так что |f’|≤hM₂ + M₀/h при любом h>0.

Можно ли этот результат распространить на векторнозначные функции?

15. Пусть f дважды дифференцируема на (0, ∞), f» ограничена на (0, ∞) и f(x)→0 при х→∞. Доказать, что f'(x)→0 при х→∞.

Указание. Применить упражнение 14 на (а, ∞). Показать, что это утверждение становится неверным, если опустить предположение о f».

16. Пусть f дифференцируема на [а, b], f(а) = 0 и существует вещественное число А, такое, что 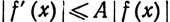на [а, b]. Доказать, что f(x) = 0 при всех х∈[а, b].

Указание. Зафиксируем х₀∈[а, b], и пусть

на сегменте [а, x₀]. Для любого х∈[а, х₀]

которая имеет два решения: f(x) = 0 и f(x) = x 2 /₄. Имеются ли другие решения?

18. Сформулировать и доказать аналогичную теорему единственности для системы дифференциальных уравнений вида

Заметим, что эту систему можно записать в виде

19. Рассмотреть частный случай упражнения 18, перейдя к системе

удовлетворяющих начальным условиям

20. Пусть f непрерывна на [а, b] и ε>0. Доказать, что существует число δ>0, такое, что

если 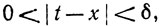a≤x≤b, a≤t≤b. (Это значит, иными словами, что f равномерно дифференцируема на [а, b], если f’непрерывна на [а, b].) Верно ли это для векторнозначных функций?

Источник

Пусть f x x2 2 докажите что

1. Окружность, центр которой расположен в первой координатной четверти, касается оси Ox в точке M, пересекает две гиперболы y = / и y = / (k_1, k_2 > 0) в точках A и B таких, что прямая AB проходит через начало координат O. Известно, что 4k_1 + k_2 = 13. Найдите наименьшую возможную длину отрезка OM.

2. Функция f(x;y), определенная на парах действительных чисел, удовлетворяет условиям f(a;a) = 0, f(a;f(b;c)) = f(a;b) + c для любых a, b, c. Найдите f(11;13,6).

3. У Васи есть кубики трех цветов. Он строит из них башню, ставя каждый следующий кубик на предыдущий. Запрещено использовать более 4 кубиков каждого из цветов. Вася заканчивает строить башню, как только в ней окажется по 4 кубиков каких-то двух цветов. Сколько различных башен может построить Вася?

4. В основании треугольной пирамиды DABC лежит равнобедренный остроугольный треугольник ABC (AC=BC). Известно, что CB > AD, а ребро DA перпендикулярно плоскости ABC. Рассматриваются проекции пирамиды DABC на плоскости, содержащие прямую AC. Известно, что наибольшая площадь такой проекции равна 39, наименьшая равна 15, а площадь треугольника ABC равна 36. Найдите объём пирамиды DABC. В ответ запишите квадрат объёма.

7. Медиана AM и высота BH треугольника ABC (H – на стороне AC) пересекаются в точке P. Найдите PH, если AM = BH = 49, MN = 19, где N – точка пересечения продолжения AM с окружностью, описанной около треугольника ABC. В ответ запишите сумму возможных значений PH.

9. Десять неотрицательных чисел таковы, что их сумма равна 4, а сумма их квадратов равна 5,2. Какое наибольшее значение может иметь самое большое из этих чисел?

10. Даны неотрицательные целые числа такие, что 24^a * 6^b * 18^c делится на 6^<100>. Найдите минимальное возможное значение a + b+ c.

Источник

Пусть f x x2 2 докажите что

СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ

Рассмотрим некоторые свойства функций непрерывных на отрезке. Эти свойства приведём без доказательства.

Функцию y = f(x) называют непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b, непрерывна соответственно справа и слева.

Теорема 1. Функция, непрерывная на отрезке [a, b], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.

Теорема утверждает, что если функция y = f(x) непрерывна на отрезке [a, b], то найдётся хотя бы одна точка x₁ Î [a, b] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x₁) ≥ f(x). Аналогично найдётся такая точка x₂, в которой значение функции будет самым маленьким из всех значений на отрезке: f(x₁) ≤ f(x).

Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x₂ и x₂‘.

Замечание. Утверждение теоремы можно стать неверным, если рассмотреть значение функции на интервале (a, b). Действительно, если рассмотреть функцию y = x на (0, 2), то она непрерывна на этом интервале, но не достигает в нём ни наибольшего, ни наименьшего значений: она достигает этих значений на концах интервала, но концы не принадлежат нашей области.

Также теорема перестаёт быть верной для разрывных функций. Приведите пример.

Следствие. Если функция f(x) непрерывна на [a, b], то она ограничена на этом отрезке.

Теорема 2. Пусть функция y = f(x) непрерывна на отрезке [a, b] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка [a, b] найдется, по крайней мере, одна точка x = C, в которой функция обращается в ноль: f(C) = 0, где a 2

а) в произвольной точке;

МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Из физики известно, что закон равномерного движения имеет вид s = v·t, где s – путь, пройденный к моменту времени t, v– скорость равномерного движения.

Однако, т.к. большинство движений происходящих в природе, неравномерно, то в общем случае скорость, а, следовательно, и расстояние sбудет зависеть от времени t, т.е. будет функцией времени.

Итак, пусть материальная точка движется по прямой в одном направлении по закону s=s(t).

Отметим некоторый момент времени t₀. К этому моменту точка прошла путь s=s(t₀). Определим скорость vматериальной точки в момент времени t₀.

Для этого рассмотрим какой-нибудь другой момент времени t₀+Δt. Ему соответствует пройденный путь s=s(t₀+Δt). Тогда за промежуток времени Δt точка прошла путь Δs=s(t₀+Δt)–s(t).

Рассмотрим отношение . Оно называется средней скоростью в промежутке времени Δt. Средняя скорость не может точно охарактеризовать быстроту перемещения точки в момент t₀ (т.к. движение неравномерно). Для того, чтобы точнее выразить эту истинную скорость с помощью средней скорости, нужно взять меньший промежуток времени Δt.

Итак, скоростью движения в данный момент времени t₀ (мгновенной скоростью) называется предел средней скорости в промежутке от t₀ до t₀+Δt, когда Δt→0:

,

т.е. скорость неравномерного движения это производная от пройденного пути по времени.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Введем сначала определение касательной к кривой в данной точке.

Пусть имеем кривую и на ней фиксированную точку М₀ (см. рисунок).Рассмотрим другую точку М этой кривой и проведем секущую M₀M. Если точка М начинает перемещаться по кривой, а точка М₀ остается неподвижной, то секущая меняет свое положение. Если при неограниченном приближении точки М по кривой к точке М₀ с любой стороны секущая стремится занять положение определенной прямой М₀Т, то прямая М₀Т называется касательной к кривой в данной точке М₀.

Т.о., касательной к кривой в данной точке М₀ называется предельное положение секущей М₀М, когда точка М стремится вдоль кривой к точке М₀.

Рассмотрим теперь непрерывную функцию y=f(x) и соответствующую этой функции кривую. При некотором значении х₀ функция принимает значение y₀=f(x₀). Этим значениям x₀ и y₀ на кривой соответствует точка М₀(x₀; y₀). Дадим аргументу x₀ приращение Δх. Новому значению аргумента соответствует наращенное значение функции y₀+Δ y=f(x₀–Δx). Получаем точку М(x₀+Δx; y₀+Δy). Проведем секущую М₀М и обозначим через φ угол, образованный секущей с положительным направлением оси Ox. Составим отношение и заметим, что .

Если теперь Δx→0, то в силу непрерывности функции Δу→0, и поэтому точка М, перемещаясь по кривой, неограниченно приближается к точке М₀. Тогда секущая М₀М будет стремиться занять положение касательной к кривой в точке М₀, а угол φ→α при Δx→0, где через α обозначили угол между касательной и положительным направлением оси Ox. Поскольку функция tg φ непрерывно зависит от φ при φ≠π/2 то при φ→α tg φ → tg α и, следовательно, угловой коэффициент касательной будет:

Т.о., геометрически у ‘(x₀) представляет угловой коэффициент касательной к графику этой функции в точке x₀, т.е. при данном значении аргумента x, производная равна тангенсуугла, образованного касательной к графику функции f(x) в соответствующей точке М₀ (x; y) с положительным направлением оси Ox.

Пример. Найти угловой коэффициент касательной к кривой у = х 2 в точке М(-1; 1).

Ранее мы уже видели, что (x 2 )’ = 2х. Но угловой коэффициент касательной к кривой есть tg α = y‘|_x=-1 = – 2.

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ

Функция y=f(x) называется дифференцируемой в некоторой точке x₀, если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x₀, то она в этой точке непрерывна.

Таким образом,из дифференцируемости функции следует ее непрерывность.

Доказательство. Если , то

,

где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

Рассмотрим на рисунке точки а, b, c.

В точке a при Δx→0 отношение не имеет предела (т.к. односторонние пределы различны при Δx→0–0 и Δx→0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к₁ и к₂. Такой тип точек называют угловыми точками.

В точке b при Δx→0 отношение является знакопостоянной бесконечно большой величиной . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – «точка перегиба» cвертикальной касательной.

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиесявертикальные касательные. Тип – «точка возврата» с вертикальной касательной – частный случай угловой точки.

Покажем, что она не имеет производной в этой точке.

Т.о., отношение при Δx→ 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x| в точке x= 0 не существует. Геометрически это значит, что в точке x= 0 данная «кривая» не имеет определенной касательной (в этой точке их две).

Следовательно, рассматриваемая функция не дифференцируема в точке x= 0. Касательная к кривой в этой точке образует с осью абсцисс угол p/2, т.е. совпадает с осью Oy.

Источник