Рабочее место цифры в числе что это
Математика. 2 класс
Конспект урока
Математика, 2 класс
Перечень вопросов, рассматриваемых в теме:
— Как образуется число 100?
— Каков разрядный состав числа 100?
Число 100 – самое маленькое трёхзначное число.
Разряд (позиция, место). Разряд является «рабочим местом» цифры в числе. Десятки, единицы – это разрядные единицы.
Единицы – это наименьший разряд в записи любого числа.
Десяток – это второй разряд в записи числа. Один десяток содержит 10 единиц.
Основная и дополнительная литература по теме урока
1. Моро М. И., Бантова М. А., Бельтюкова Г. В. и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1. – 8-е изд. – М.: Просвещение, 2017. – С.12
2. Волкова А. Д. Математика. Проверочные работы. 2 кл.: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2017 – С. 4-7
3. Волкова С. И. Математика. Устные упражнения. 2 кл.: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2018 – С. 9
Теоретический материал для самостоятельного изучения
Найдем устно значения выражений и определим лишнее:
Лишнее выражение 60 + 40 = 100, так как его значение равно 100, а всех других выражений числу 90.
Положим на парту девять десятков палочек. Сколько это единиц? 90
Добавим ещё один десяток.
Стало 10 десятков или 100 единиц
Цифра 1 в числе 100 обозначает одну сотню.
Число 100 трехзначное. В нем 3 цифры, 3 знака
Запишем все пары «круглых» двузначных чисел, в результате сложения которых получается число сто.
Разряды и классы чисел по математике — что это?
В начальных классах дети изучают «Разряды и классы чисел», однако эта тема вызывает много вопросов у родителей.
В этой статье Вы сможете «освежить» свои знания и объяснить ребенку эту тему.
Числа и цифры
ЧИСЛА — это единицы счёта. С помощью чисел можно сосчитать количество предметов и определить различные величины (длину, ширину, высоту и т. д.).
Для записи чисел используются специальные знаки — ЦИФРЫ.
Цифр десять: 1 2 3 4 5 6 7 8 9 0
Натуральные числа
НАТУРАЛЬНЫЕ ЧИСЛА — это числа, которые используются при счёте.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …,
1 — самое маленькое число, а самого большого числа не существует.
Число 0 (нуль) обозначает отсутствие предмета. Нуль НЕ является натуральным числом.
Разряды и классы натуральных чисел
Для записи чисел используется ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ. В десятичной системе счисления пользуются единицами, десятками единиц, десятками десятков — сотнями и т. д.
Каждая новая единица счёта больше предыдущей ровно в 10 раз:
Десятичная система счисления — позиционная. В этой системе счисления значение каждой цифры в записи числа зависит от её позиции (места).
Позиция (место) цифры в записи числа называется РАЗРЯДОМ. Самый младший разряд — ЕДИНИЦЫ. Затем следуют ДЕСЯТКИ, СОТНИ, ТЫСЯЧИ и т. д.
Каждые три разряда натуральных чисел образуют КЛАСС.

Основной вопрос, который родители часто задают: зачем ребенку эти знания? Ответ на этот вопрос очень простой — после изучения этого материала, дети переходят к таким темам как сложение и вычитание в столбик, где обязательно необходимо знать разряды числа, чтобы правильно вычислить примеры.
И если ребенок не освоит эту тему, тогда он не сможет правильно решать в столбик.
Складываем и вычитаем через разряды
Сложение столбиком

Записываем под единицами.
Б) Складываем десятки: 4 + 3 = 7.
Записываем под десятками.
В) Складываем сотни: 4 + 3 = 7.
Записываем под сотнями.
Ответ: 777
Вычитание столбиком

Записываем под единицами.
Б) Вычитаем десятки: 0 меньше,
чем 2, занимаем в сотнях (тысячах).
10 – 2 = 8. Записываем под десятками.
В) Вычитаем сотни: 9 – 4 = 5.
Записываем под сотнями.
Ответ: 586
Как вести себя родителям при детских ссорах?
Статья о грамотном поведении родителей при детских ссорах. Читать далее
Сумма разрядных слагаемых
Сумма разрядных слагаемых
Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых. Сумму разрядных слагаемых можно записать следующим образом:
35 = 3 десятка + 5 единиц = 3*10 = 30 + 5 = 35.
30 — разрядное слагаемое; 5 — разрядное слагаемое.
86 = 8 десятков + 6 единиц = 8*10 = 80 + 6 = 86
80 — разрядное слагаемое; 5 — разрядное слагаемое.
356 = 3 сотни + 5 десятков + 6 единиц = 3*100 + 5*10 + 6 = 300+50+6 = 356.
300, 50, 6 — разрядные слагаемые.
Разряды и классы чисел
Чтобы без труда записывать числа в виде суммы разрядных слагаемых, нужно безошибочно определять класс и разряд числа.
В многозначном числе цифры справа налево разбиваются на группы по три цифры. Такие группы называют классами.
Названия классов многозначных чисел:
Чтобы чтение многозначного числа не превращалось в головоломку, при записи лучше разграничивать число по классам. Вот так:
Читаться такое число будет слева направо: триста сорок пять миллиардов четыреста шестьдесят шесть миллионов сто двадцать девять тысяч триста пятьдесят.
Разряд — это место, которое занимает цифра в записи многозначного числа.
Разряды считаются справа налево. Первая цифра справа в записи числа относится к первому разряду.
Разрядные единицы — это единицы, десятки, сотни, тысячи, миллионы.
Все разрядные единицы, за исключением простых единиц, — составные единицы. Каждые десять единиц одного разряда составляют одну единицу следующего разряда.
Если составная единица больше другой единицы — она называется единицей высшего разряда. Если меньше, то единицей низшего разряда. Так, например, сотня — единица высшего разряда относительно десятка, но низшего разряда относительно тысячи.
Чтобы выяснить сколько всего в числе единиц определенного разряда, нужно мысленно вычеркнуть из числа все цифры низшего разряда.
Это значит, нужно выяснить, сколько сотен заключается в тысячах и в сотнях этого числа. 5689 — на третьем месте в классе единиц стоит цифра 6, значит в числе есть 6 сотен. Следующая влево цифра — 5 (тысячи). 1 тысяча = 10 сотен. 5 тысяч = 50 сотен. Всего в числе 56 сотен.
Если в разряде стоит цифра 0, то это означает отсутствие единиц, десятков, сотен и т.д., в зависимости от того, где именно содержится цифра.
Иногда бывает необходимо не только разложить число на разрядные слагаемые, но и определить количество единиц какого-то определенного разряда.
В такой ситуации можете выполнить подробный разбор числа.
Шесть миллионов пятьдесят семь тысяч триста восемьдесят шесть
6 057 386 = 6 * 1 000 000 + 0 * 100 000 + 5 * 10 000 + 7 * 1000 + 3 * 100 + 8 * 10 + 6 = 6 000 000 + 50 000 + 7 000 + 300 + 80 + 6.
Из чего состоит это число? Из:
Для того, чтобы алгоритм разложения числа на простые слагаемые был всегда под рукой, сохраняйте себе табличку с примером. В ней вы найдете вопросы, которые помогут разложите любое число.
Определите, сколько единиц в числе 5 068 252.
1. Определяем сколько всего единиц в числе.
2. Определяем количество десятков.
Записываем число без первого разряда (единицы).
3. Определяем количество сотен.
Записываем число без первого
и второго разрядов (десятки и сотни).
4. Определяем количество единиц тысяч.
Записываем число без первого, второго,
третьего разрядов (единицы, десятки, сотни).
5. Определяем количество десятков тысяч.
Записываем число без первого, второго, третьего,
четвертого разрядов (единицы, десятки, сотни, единицы тысяч).
6. Определяем количество сотен тысяч.
Записываем число без десятков тысяч, единиц тысяч,
сотен и единиц.
7. Определяем количество единиц миллионов.
Записываем число без сотен тысяч, десятков тысяч,
единиц тысяч, сотен, десятков, единиц.
Расписав таким образом число, мы выяснили, что в числе 5 068 252: 5 единиц класса миллионов (3 класс); 68 единиц класса тысяч (2 класс); 252 единицы класса единиц (1 класс).
Может показаться, что такой подробный разбор ни к чему, что и без того все понятно, но многоразрядные многозначные числа — коварны. Лучше хорошенько потренироваться, используя все вспомогательные материалы, как эта табличка, а потом уже раскладывать любое число за секунды и в уме.
Примеры
Внимательно просмотрите примеры и попробуйте самостоятельно представить числа в виде суммы разрядных слагаемых.
Представьте в виде суммы разрядных слагаемых:
Как видите, все довольно просто. Занятие весьма успокаивающее, медитативное. Приятно сесть после тяжелого дня и пораскладывать числа на разрядные слагаемые.
Если вдруг так вышло, что вы не расслабляетесь при виде цифр, то воспользуйтесь онлайн-калькулятором. В интернете таких калькуляторов немало, вот один из них.
Так вы сможете разложить на разрядные слагаемые любое, даже самое гигантское, число. Важно разобраться в разрядах и классах чисел, тогда вы точно ничего не перепутаете.
Правило первой цифры
Возьмите какой-нибудь справочник о нашем мире. Пусть это будет географический атлас. Посмотрите на данные по численности населения разных стран. Или на характеристики рек: длину и площадь бассейна. Точнее, смотреть надо на первые цифры этих чисел. Окажется, что в этих совокупностях данных первые цифры распределены совсем не равномерно (как, возможно, вы ожидали): например, единица будет встречаться гораздо чаще, чем в 1/9 случаев, и вообще — чаще других цифр. Так, в списке стран по населению единица стоит на первом месте в 66 случаях из 242. Это примерно 27%. Если набор данных достаточно большой, то следующей по частоте цифрой будет двойка, потом — тройка и т. д. Оказывается, что такой же эффект наблюдается и у многих других наборов чисел, которые возникают естественным путем. Причем этот эффект не зависит от того, в каких единицах измерять данные.
Задача
Предположим, что имеется очень большой набор чисел, про который известно, что он обладает описанными выше свойствами (на первом месте единицы встречаются чаще двоек, двойки — чаще троек и т. д., и это не зависит от выбранной системы измерения). Определите вероятности, с которыми случайно взятое число из этого набора будет начинаться на 1, 2, …, 9.
Подсказка
Пусть число x начинается на какую-нибудь данную цифру, скажем на 5. Как это можно описать по-другому? Например, так: это число не меньше, чем какое-то число вида 50. 0, но не больше, чем 59. 9 (в первом случае вместо многоточия стоит сколько-то нулей, во втором — столько же девяток). В виде неравенства это выглядит так:
Но более удобно переписать это в виде
Или, что то же самое
где n — количество нулей после значащих цифр в предыдущем неравенстве.
Обобщая это рассуждение, получаем такой вывод: данное число x начинается на цифру i, если (и только если) при некотором целом неотрицательном n выполнено неравенство
Теперь уже можно приступать к вычислению искомых вероятностей. Фактически, осталось только прологарифмировать последнее неравенство (опять же, для удобства) и правильно проинтерпретировать то, что получится.
Решение
Проделав действия, описанные в подсказке, мы можем представить утверждение число x начинается с цифры i в виде двойного неравенства
Взяв логарифм по основанию 10 (который обозначается буквами lg), перепишем его так:
Наконец, взяв дробную часть, получим такие неравенства:
Тут стоит пояснить, что поскольку i — какая-то цифра от 1 до 9, то числа lg i и lg(i + 1) лежат между 0 и 1. А n — целое неотрицательное число, и после взятия дробной части оно просто исчезает.
Подведем промежуточный итог. Получилось, что число x начинается на цифру i если и только если дробная часть его логарифма лежит между lg i и lg(i + 1).
Эту ситуацию удобно рассмотреть на рисунке. Дробная часть любого числа всегда принадлежит полуинтервалу [0; 1). Ему же, как отмечалось выше, принадлежат и числа вида lg i, где i — цифра. Отметим их все на этом промежутке:
Дробные части логарифмов чисел из нашего набора как-то разбросаны по этому промежутку. Осталось понять, как именно.
Соединим концы промежутка и представим его в виде окружности длины 1 (скоро станет понятно, зачем это делается):
Отмеченные точки («логарифмы цифр») делят эту окружность на дуги, и теперь нужно понять, как числа из набора распределятся по этим дугам.
Осталось вспомнить, что распределение чисел набора по первой цифре не зависит от выбора единиц измерения (это свойство не должно казаться противоестественным для обсуждаемой ситуации: логично предположить, что распределение зависит от того, откуда взялись данные, от их природы, а не от того, как их измерять). Смена единиц измерения («смена масштаба») — это просто умножение всех чисел набора на один и тот же множитель. Например, чтобы перевести футы в метры, нужно умножить на 0,3048 — ровно столько метров в одном футе. То есть любое число x из набора превратится в число kx после перемасштабирования (буквой k обозначен этот «масштабный» множитель). Но на окружности мы следим за дробными частями от логарифмов чисел набора, поэтому после смены масштаба мы будем иметь дело с числами вида
Послесловие
Исследованный в этой задаче эффект в распределении чисел по первой цифре называется законом Бенфорда (Benford’s law). Хотя впервые его обнаружил почти за 50 лет до Бенфорда астрономом Саймон Ньюком. Эта история довольно любопытна. В те времена для расчетов использовались различные готовые таблицы со значениями основных функций, это были толстые тома. Однажды, когда ему потребовались таблицы логарифмов, Ньюком обратил внимание, что первые страницы испачканы и потрепаны гораздо сильнее. И чем ближе к концу справочника, тем чище и новее были страницы. Значит, решил Ньюком, его коллегам чаще всего нужны значения логарифмов чисел, которые начинаются с единицы. А числа, начинающиеся с двойки, нужны реже, с тройки — еще реже, и т.д. То есть сами числа встречаются с разной частотой в зависимости от своей первой цифры. Этот вывод, а также найденное логарифмическое распределение (которое мы получили в решении) Ньюком опубликовал в 1881 году. Но на его заметку почти не обратили внимания, и вскоре она была забыта.
В 1938 году этот же результат опубликовал Франк Бенфорд, инженер компании General Electric, который обнаружил эту закономерность почти так же, как и Ньюком, — просматривая численные таблицы. Но Бенфорд сделал гораздо больше. За несколько лет он изучил порядка 20 000 разных совокупностей чисел, которые он брал из всех возможных источников: различных справочников, статистических сводок и даже просто из газет (буквально: все числа, которые встречаются в одном номере газеты). И почти всегда распределение по цифрам получалось близким к логарифмическому (или хотя бы похожим на него, если чисел было мало).
Стоит отметить, что закон Бенфорда работает далеко не всегда. Например, если в качестве наборов брать номера лотерейных билетов или почтовые индексы или телефонные номера, то ничего не выйдет: везде будет равномерное распределение — на каждую цифру будет начинаться примерно одинаковое количество чисел. Тут дело в том, что числа в этих совокупностях довольно строго ограничены, а в таком случае закон Бенфорда не работает.
А когда же он работает? Как видно из решения, важно, чтобы распределение по цифрам не зависело от единиц измерения, то есть не менялось от умножения всех чисел набора на один тот же множитель. Если это свойство — «независимость от масштаба» — выполняется, то закон работает. Правда, это не очень удобный критерий. Некоторое время назад американский математик Т. Хилл доказал, что если есть несколько разных наборов таких чисел и из каждого взять какую-нибудь часть и объединить эти части в новый набор, то для него закон Бенфорда тоже будет работать. Подробнее об этом можно почитать на английском в статьях Хилла: The First Digit Phenomenon (это небольшая обзорная статья, PDF, 113 Кб) и A basic theory of Benford’s Law (PDF, 1,3 Мб).
Закон работает и для некоторых последовательностей чисел, которые появляются в математике и про которые трудно сказать, что они «возникают естественным путем», то есть из жизни. Это, например, последовательности степеней двойки, факториалов, чисел Фибоначчи. А вот последовательность самих натуральных чисел закону Бенфорда не подчиняется. Рекомендую также почитать статью В. И. Арнольда Статистика первых цифр степеней двойки и передел мира (PDF, 500 Кб), в которой делается попытка объяснить, почему закон Бенфорда работает для данных по населению стран и по их площади.
Любопытно, что в конце XX века этот, на тот момент в общем-то эмпирический, закон (точнее, методы на его основе) стали успешно применять в аудите и при расследовании финансовых махинаций, а также при проверке разного рода социологических исследований. Один из таких случаев описан в книге Л. Млодинова «(Не)совершенная случайность». Речь идет об аферисте, который сначала умудрился собрать с инвесторов около 90 млн долларов на открытие сети клубов здоровья, а затем, вместо того чтобы заниматься этим бизнесом и развивать его, растранжирил почти все деньги. Для прикрытия своих делишек он вместе с подельниками устроил сложную схему с большим количеством подставных счетов, между которыми переводились деньги имитируя нормальную деятельность активно расширяющейся компании. Афера вскрылась после того, как в ходе анализа этих переводов выяснилось, что первые цифры распределены не по закону Бенфорда: преступники «рисовали» числа в переводах, не зная про этот закон.
Разряды и классы чисел
Числа и цифры
Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.
Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.
Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определенное место — позицию.
Классы чисел
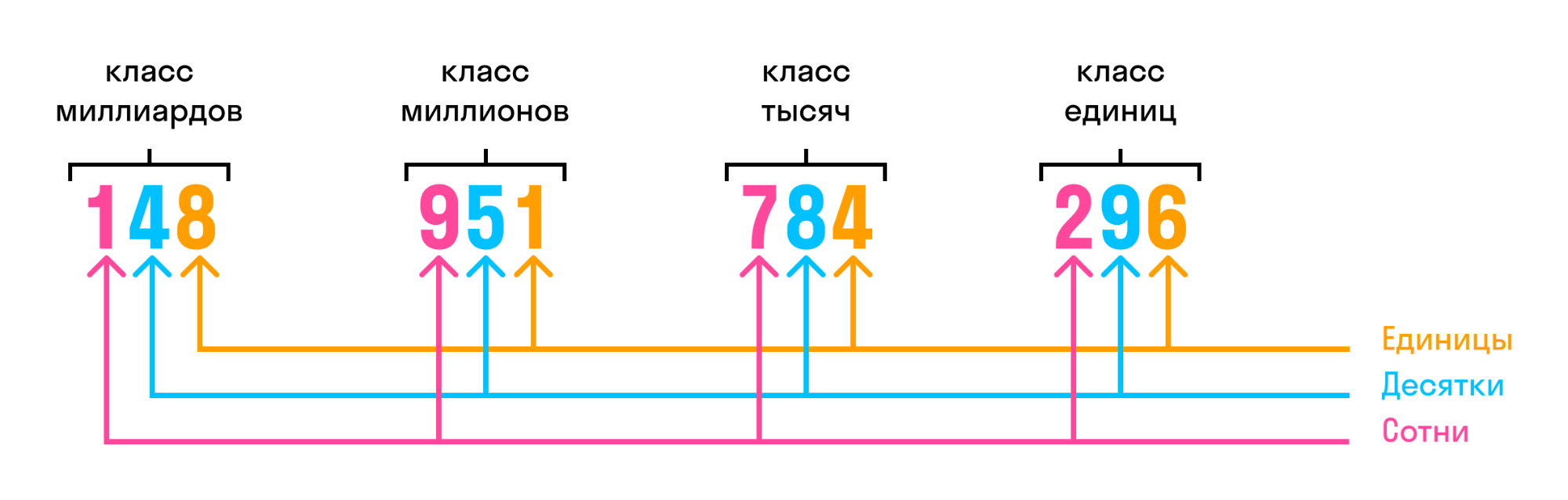
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.
Названия классов многозначных чисел справа налево:
Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
А теперь прочитаем число единиц каждого класса слева направо:
Разряды чисел
От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.
Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще чтобы визуально разделить классы чисел.
Разрядные единицы обозначают так:
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Чтобы легче понимать математику — записывайтесь на наши курсы по математике!
Потренируемся
Пример 1. Записать цифрами число, в котором содержится:
Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.
Пример 2. Сколько сотен содержится в числе 6284?
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.
Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.
Значит, в данном числе содержится 62 сотни.
Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.
Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.