Расчетное сопротивление в чем измеряется

Расчетное сопротивление в чем измеряется

Итак, давайте разбираться, зачем понадобилось ломать школьную линейку, оставляя детей без школьных принадлежностей, и чем это может нам помочь. Пришло время добавить к наглядности несколько формул, тут все будет почти так же просто и понятно, как и в первой части сопромата для чайников, но понадобятся знания математики на уровне 4-5 классов и начальные знания по геометрии.

Основы сопромата, расчет прогиба балки

Часто при расчете строительных конструкций важно определить не только геометрические параметры сечения конструкции, но и величину прогиба конструкции с точностью до миллиметра. Дело в том, что величина прогиба для любой конструкции нормируется различными СНиПами и не должна превышать 1/250 для балок междуэтажных перекрытий, 1/200 для чердачных перекрытий и перемычек и так далее, список длинный. Когда расчет производится для себя (например строится частный дом и нужно сделать балки перекрытия или перемычки), то определять величину прогиба не обязательно, никто Вас ругать не будет, главное чтобы по несущей способности расчет был верный, но все же определить прогиб конструкции желательно. Ведь знание величины прогиба позволить более точно выбрать, например, вариант отделки потолка.

Сопромат для чайников

По большому счету основы теории сопротивления материалов (сопромата) даже проще, чем таблица умножения. Таблица умножения большая, ее нужно тупо заучить как «Отче наш», а основы сопромата сводятся к нескольким основным положениям, которые достаточно легко наглядно продемонстрировать и потому их легко запомнить даже абсолютному «чайнику» в сопромате.

Обстоятельства сложились так, что вступительный курс лекций по сопромату я пропустил, так как вернулся после службы на флоте в институт за 2 недели до сессии, поэтому основы сопромата пришлось постигать самому, за что самый суровый и неподкупный препод на потоке, заваливший не одну сотню студентов, поставил мне пятерку. Ну и понеслось, преподаватели, видя пятерку по сопромату, ставить меньшую отметку по своему предмету не решались и в итоге у меня получился красный диплом.

Впрочем не будем отвлекаться, а вернемся к основам в изложении такого же чайника, как и некоторые из вас.

Приведение сосредоточенной нагрузки к эквивалентной равномерно распределенной

Это в свою очередь означает, что расчет нужно вести по разным формулам, например, определять максимальное значение изгибающего момента отдельно для равномерно распределенной нагрузки и отдельно для сосредоточенных нагрузок. То же касается и определения максимального прогиба конструкции. Хорошо, если такая сосредоточенная нагрузка только одна, расчеты при этом не сильно усложнятся, а вот если таких сосредоточенных нагрузок несколько, да еще и приложены они на разных расстояниях друг от друга и несимметрично, то расчет становится достаточно сложным. Между тем, чем больше на строительную конструкцию действует сосредоточенных нагрузок, тем ближе суммарная эпюра моментов от этих сосредоточенных нагрузок к эпюре от равномерно распределенной нагрузки. Поэтому для упрощения расчетов конструкций постоянного по длине сечения вполне допустимо заменять сосредоточенные нагрузки на эквивалентную равномерно распределенную. Однако делать это нужно осторожно, так как варианты приложения сосредоточенных нагрузок бывают разные:

Виды опор, какую расчетную схему выбрать

Основы сопромата. Определение касательных напряжений.

Основы сопромата, момент сопротивления

Расчет на растяжение стержня

Расчет на прочность прямолинейного стержня при действии центрально приложенной растягивающей силы является одной из самых простых задач в теории сопротивления материалов.

Смысл данного расчета сводится к тому, чтобы обеспечить необходимую прочность материала, исходя из условия:

Приведение неравномерно распределенной нагрузки к эквивалентной равномерно распределенной

Иногда при расчете конструкций, на которые действует симметричная распределенная нагрузка, описываемая достаточно сложными уравнениями, возникает необходимость привести данную нагрузку к эквивалентной равномерно распределенной для упрощения этих самых расчетов.

Так например, все мы знаем, что максимальный изгибающий момент при действии равномерно распределенной нагрузки на шарнирно опертую балку будет в середине пролета (l/2) и составит:

Что такое жесткость и гибкость элементов

Разницу в работе гибких и жестких стержней под воздействием нагрузки люди заметили достаточно давно. Так один из мастеров восточных единоборств, гуляя по зимнему саду, сделал примерно следующий вывод: жесткая сухая ветка под тяжестью налипшего снега ломается, а гибкая ветка прогибается и, сбросив налипший снег, возвращается в прежнее положение с минимумом повреждений.

Если перевести это гибкую поэтическую аллегорию, помогавшую мастеру восточных единоборств привлекать новых учеников, на современный жесткий язык теории сопротивления материалов, то звучать это будет примерно так: если напряжения в рассматриваемом поперечном сечении жесткого элемента конструкции превышают значение нормативного сопротивления, то это приведет сначала к значительным пластическим деформациям, а затем, при увеличении напряжений, и к разрушению жесткого элемента (будет это разрушение хрупким или вязким, принципиального значения не имеет). В то же время гибкий элемент конструкции под действием такой же нагрузки, не разрушится, но потеряет устойчивость.

Какой момент инерции выбрать?

В последнее время мне все чаще задают вопрос: какой момент инерции выбрать для расчетов балки и почему? А после этого добавляют примерно следующее: «во всех учебниках сопромата пишут только, что сечение должно стремиться к квадрату, но в жизни часто встречается двутавр, например» или «всюду пишут, что сечение должно стремиться к квадрату и брать надо наименьший момент инерции. Никак не могу ухватить за хвост физический смысл, можно это как-то на пальцах истрактовать?».

Момент силы

Формула для определения момента силы на удивление проста:

Момент инерции, куда пропала скорость?

Статья получилась достаточно большой. Я, хоть и не Толстой Л.Н., но тоже люблю разливаться мыслью по древу, но некоторые моменты все равно оказались упущены или недостаточно акцентированы, что у некоторых, хотя далеко не у всех читалей вызывает вопросы.

Формула прогиба

В статье «Расчетные схемы для балок» задается достаточно много вопросов и делается достаточно много комментариев на тему правильности той или иной формулы. Как правило я отвечаю на вопросы там же в комментариях, но на этот раз тема неординарная и я решил вынести ее в отдельную статью. К тому же в комментариях степень числа можно отобразить только как ^, а это затрудняет восприятие.

Сначала приведу переписку из комментариев касательно правильности формулы прогиба:

Музыкальная теория расчета гибких нитей (Часть 1)

Но если один из родителей еще и разбирается в сопромате, то, увидев столь вольное обращение с гитарой, может ребенка и наказать. Причем очень строго: за грубое нарушение теории расчета гибких нитей. Вот так! Не меньше!

Итак, маленькая теоркомедия в 4 актах.

Акт первый

Мы начинаем прикладывать условно сосредоточенную нагрузку Q к струне в центре тяжести гитары, на расстоянии l/2 от опор.

Источник

Нормативные и расчетные сопротивления

Основными характеристиками сопротивления материалов силовым воздействиям являются нормативные сопротивления Rтн Rвн устанавливаемые нормами проектирования строительных конструкций.

Механические свойства материалов изменчивы, поэтому нормативные сопротивления устанавливают на основе статистической обработки показателей механических свойств материалов, выпускаемых нашей промышленностью. Значения нормативных сопротивлений устанавливают такими, чтобы обеспеченность их составляла не менее 0,95.

Значение нормативного сопротивления стали равно значению контрольной или браковочной характеристики, устанавливаемой соответствующими государственными стандартами и имеет обеспеченность не менее 0,95.

Для углеродистой стали и стали повышенной прочности и алюминиевых сплавов за основную характеристику нормативного сопротивления принято значение предела текучести, поскольку при напряжениях, равных пределу текучести, в растянутых, изгибаемых и других элементах начинают развиваться пластические деформации, а сжатые элементы начинают терять устойчивость.

Расчетные сопротивления материала.

Расчетные сопротивления материала R и Rв определяют делением нормативного сопротивления на коэффициент надежности по материалу:

Нормативное сопротивление стали

Расчетное сопротивление материала – сопротивление, используемое в расчетах строительных конструкций и оснований и определено по формуле:

— нормативное сопротивление материала;

— коэффициент надежности по материалу.

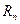
Обеспеченность нормативного сопротивления стали равно 0,95 (это значит, что из 100 образцов 5 образцов имеют сопротивление ниже нормативного).

Виды нормативных сопротивлений стали:

-) — предел текучести стали равный по ГОСТам и ТУ;

-) — временное сопротивление равное по ГОСТам и ТУ.

Виды расчетных сопротивлений стали:

-) — расчетное сопротивление стали на растяжение, сжатие и изгиб по пределу текучести;

-) — расчетное сопротивление стали на растяжение, сжатие и изгиб по временному сопротивлению;

-) — расчетное сопротивление стали на срез.

Расчетное сопротивление , определяются по таблице 51 * СНиПа в зависимости:

-) от вида проката (листовой, фасонный);

-) от толщины элемента

Нагрузки и воздействия

зависимости от продолжительности дейст­вия нагрузок следует различать постоянные и вре­менные (длительные, кратковременные, особые) нагрузки.

Нагрузки, возникающие при изготовлении, хранении и перевозке конструкций, а также при воз­ведении сооружений, следует учитывать в расчетах как кратковременные нагрузки.

К постоянным нагрузкам следует относить:

а) вес частей сооружений, в том числе вес несу­щих и ограждающих строительных конструкций;

б) вес и давление грунтов (насыпей, засыпок), горное давление.

Сохраняющиеся в конструкции или основании усилия от предварительного напряжения следует

учитывать в расчетах как усилия от постоянных нагрузок.

К длительным нагрузкам следует относить:

а) вес временных перегородок, подливок и подбетонок под оборудование;

б) вес стационарного оборудования: станков, аппаратов, моторов, емкостей, трубопроводов с ар­матурой, опорными частями и изоляцией, ленточ­ных транспортеров, конвейеров, постоянных подъ­емных машин с их канатами и направляющими, а также вес жидкостей и твердых тел, заполняющих оборудование;

в) давление газов, жидкостей и сыпучих тел в емкостях и трубопроводах, избыточное давление и разрежение воздуха, возникающие при вентиляции шахт;

г) нагрузки на перекрытия от складируемых материалов и стеллажного оборудования в склад­ских помещениях, холодильниках, зернохранили­щах, книгохранилищах, архивах и подобных поме­щениях;

д) температурные технологические воздействия от стационарного оборудования;

е) вес слоя воды на водонаполненных плоских покрытиях;

ж) вес отложений производственной пыли, если ее накопление не исключено соответствующими мероприятиями;

з) нагрузки от людей, животных, оборудования на перекрытия жилых, общественных и сельскохо­зяйственных зданий с пониженными нормативными значениями, приведенными в табл. 3;

и) вертикальные нагрузки от мостовых и подвес­ных кранов с пониженным нормативным значением, определяемым умножением полного нормативного значения вертикальной нагрузки от одного крана (см. п. 4.2) в каждом пролете здания на коэффи­циент: 0,5 — для групп режимов работы кранов 4К—6К; 0,6 — для группы режима работы кранов 7К; 0,7 — для группы режима работы кранов 8К. Группы режимов работы кранов принимаются по ГОСТ 25546-82;

л) температурные климатические воздействия с пониженными нормативными значениями, опреде­ляемыми в соответствии с указаниями пп. 8.2—8.6 при условии θ₁ = θ₂ = θ₃ = θ ₄ = θ ₅ = 0, Δ_I = Δ_VII = 0;

м) воздействия, обусловленные деформациями основания, не сопровождающимися коренным из­менением структуры грунта, а также оттаиванием вечномерзлых грунтов;

н) воздействия, обусловленные изменением влажности, усадкой и ползучестью материалов.

. К кратковременным нагрузкам следует от­носить:

а) нагрузки от оборудования, возникающие в пускоостановочном, переходном и испытательном режимах, а также при его перестановке или замене;

б) вес людей, ремонтных материалов в зонах обслуживания и ремонта оборудования;

в) нагрузки от людей, животных, оборудования на перекрытия жилых, общественных и сельскохо­зяйственных зданий с полными нормативными значениями, кроме нагрузок, указанных в п. 1.7а, б, г, д;

г) нагрузки от подвижного подъемно-транспорт­ного оборудования (погрузчиков, электрокаров, кранов-штабелеров, тельферов, а также от мосто­вых и подвесных кранов с полным нормативным значением);

д) снеговые нагрузки с полным нормативным значением;

е) температурные климатические воздействия с полным нормативным значением;

ж) ветровые нагрузки;

з) гололедные нагрузки.

К особым нагрузкам следует относить:

а) сейсмические воздействия;

в) нагрузки, вызываемые резкими нарушениями технологического процесса, временной неисправ­ностью или поломкой оборудования;

г) воздействия, обусловленные деформациями основания, сопровождающимися коренным изме­нением структуры грунта (при замачивании просадочных грунтов) или оседанием его в районах горных выработок и в карстовых.

Нормативные и расчётные сопротивления стали

Значение нормативного сопротивления стали равно значению конт­рольной или браковочной характеристики, устанавливаемой соответст­вующими государственными стандартами и имеет обеспеченность не менее 0,95. Установлены два вида нор­мативных сопротивлений — по пределу текучести R_Т Н =υ_Т и временно­му сопротивлению R_В Н =υ_В. В соответствии со стандартом значения предела текучести и времен­ного сопротивления имеют обеспеченность в пределах 0,95—0,995.Значения υ_Т и υ_В являются браковочными и при приемке проката контролируются, являющиеся нормативными сопротив­лениями. Расчетные сопротивления материала R и R_B определяют делени­ем нормативного сопротивления на коэфф. надежности по ма­териалуγ_mR= R_Т Н / γ_m R_В= R_В Н / γ_m. Коэффициент надежности по материалам γ_m. Значение механичес­ких свойств металлов проверяется на металлургических заводах выбо­рочными испытаниями. Механические свойства металлов контролиру­ют на малых образцах при кратковременном одноосном растяжении, фактически же металл работает длительное время в большеразмерных конструкциях при сложном напряженном состоянии. При расчете конструкций с использованием расчетного сопротивле­ния, установленного по временному сопротивлению, вводится допол­нительный коэфф. надежности γ_m=1,3.

Методики расчёта ИК

Все расчеты делятся на две группы — статические (или силовые) и конструктивные. Цель силовых расчетов — определить усилия, действующие в конструкции (системе) и в каждом элементе, или, как говорят, определить игру сил. Этим занимается строительная механика. Цель конструктивных расчетов — подтвердить, что при принятых размерах сечений ни одно возможное предельное состояние не наступит. Есть и третья цель — обеспечение путем обоснованного выбора габаритов элемента н размеров сечений минимума расхода металла или иных экономических показателей. Для этого используется раздел строительной механики — теория оптимального проектирования. При выполнении конструктивных расчетов в соответствии с техническими требованиями выполняются три основных проверки — прочности, общей устойчивости, жесткости (гибкости). Проверка прочности: в форме проверки напряжений σ= N/Ф_н ≤R_yγ_c ; в форме проверки несущей способности N≤ Ф_нR_yγ_c ; в форме проверки отношения действующего силового фактора (N) и несущей способности N/( Ф_нR_yγ_c)≤1, где Ф_н— геометрический фактор нетто, т. е. с учетом ослабления сечениа, если таковое имеется. Проверка устойчивости (формы):в виде проверки напряжений σ≤ σ_ср или σ= N(ϕ_tФ)≤ R_yγ_cр где σ_ср — критическое напряжение для элементов, у которых сжатие возникает при разных видах работы — внентральное сжатие, внецентренное, иэгиб; ϕ_t — коэф- ициент устойчивости при указанных видах работы.

Проверка жесткости (гибкости):

f/l≤[f/l]— общая деформация; f/l — относительная дефор- ация (мера деформативности); [f/l]—предельная от- эсительная деформация;

Источник

СНиП 2.03.06-85 Алюминиевые конструкции (с Изменениями)

3. РАСЧЕТНЫЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ И СОЕДИНЕНИЙ

3.1. Расчетные значения сопротивления (расчетные сопротивления) алюминия и литейного алюминия для расчетных температур наружного воздуха от плюс 50 до минус 65 °С приведены в табл. 5 и 6, при этом расчетные сопротивления сдвигу и смятию установлены в соответствии с табл. 4 с округлением значений расчетных сопротивлений до 5 МПа (50 кгс/кв.см).

Растяжение, сжатие и изгиб

Смятие торцевой поверхности (при наличии пригонки)

Смятие местное при плотном касании

— нормативное сопротивление алюминия разрыву, принимаемое равным минимальному значению временного сопротивления по государственным стандартам и техническим условиям на алюминий;

Источник

Показатели нормативного и расчетного сопротивления бетона

Любая бетонная конструкция должна переносить определенные в технической документации нагрузки в течение длительного времени без разрушений. В строительных проектах указываются основные характеристики, к которым относятся плотность, показатели расчетного сопротивления бетона, морозоустойчивость, водонепроницаемость. Проблема состоит в том, что даже самый качественный бетон неоднороден. Элементы имеют различные геометрические размеры и сечения, поэтому разные участки сооружения могут иметь неодинаковые свойства. Для уточнения характеристик материала вводится методика вычисления прочности.

Что такое расчетное сопротивление?

Расчетное сопротивление бетонной смеси – характеристика отражающая свойство материала противостоять внешним механическим нагрузкам. Его применяют при проектировании зданий и сооружений. Данный показатель получают из нормативных значений противодействия конкретной марки раствора делением на специальный коэффициент.

Этот коэффициент, применяемый для вычисления расчетного сопротивления бетона на сжатие обозначается γ_b и может принимать значения:

Коэффициенты надежности материала при механическом растяжении обозначаются γ_bt, они могут быть равны:

Классы бетонов обозначаются от В10 до В60, значения их нормативного противодействия приводятся в специальных таблицах.

Как получить расчетное сопротивление?

Для получения расчетного сопротивления бетона по осевому сжатию определяется класс материала, из таблицы берутся его нормативные данные и производится вычисление по формуле:

Аналогично рассчитывают расчетное сопротивление бетона осевому растяжению:

где R_bt – расчетные значения на осевое растяжение, множитель R_btn – нормативные показатели на растяжение, γ_bt – коэффициент для растяжения.

Учитывая условия, в которых будут эксплуатироваться бетонные конструкции, вводятся и другие коэффициенты γ_bi, учитывающие эти особенности:

Нормативное сопротивление

До 2001 года единственной характеристикой бетона указывающей на противодействие механической силе, считалась марка, обозначавшаяся буквой «М». Теперь, согласно СНиП 2.03.01 введена другая характеристика, так называемый класс прочности, обозначающаяся буквой «В». Для определения свойств железобетонных и бетонных конструкций были предложены нормативы, согласно СП 52-101-2003.

Для определения класса раствор заливают в куб с ребром 150 мм. Уплотняют его в форме и дают полностью затвердеть при температуре 18-20ºС в течение 28 суток. После этого образец поступает на испытание, и разрушается на специальном прессе. Сопротивление бетона осевой нагрузке, выраженное в МПа и является свойством, по которому определяется данная характеристика. Иногда для определения класса берется призменный образец, высота которого в четыре раза больше ребра основания.

Дополнительно образец подвергается проверке на осевое растяжение, который тоже необходимо учитывать при проведении вычислений.

При правильном определении класса не требуется делать дополнительных испытаний, поскольку они уже занесены в специализированные таблицы.

Используя эти таблицы можно, имея данные на сжатие, сразу определить показатели и на растяжение. По ним ясно видно – этот параметр для любого бетона на растяжение гораздо меньше, чем на сжатие, это обязательно учитывается при проектировании.

Эти параметры для различного класса прочности сводятся в специальную таблицу. Значения могут меняться в зависимости от условий определяемых соответствующими коэффициентами:

Из таблицы видно, что расчетное значение ниже нормативного, поскольку учитывает сторонние факторы, тип воздействия на бетонную конструкцию, возможную неоднородность материала, центр тяжести контура.

График Зависимости напряжений от деформаций

При определении характеристик железобетонных конструкций применяют методику моделирования наклонных сечений. Учитывается толщина и тип арматуры, отдельно рассчитывается ее прочность.

Заключение

Сопротивление бетона рассчитывается в зависимости от действия на него различных сил, которые могут быть сжимающими, поперечными, изгибающими, а также под местным сжатием. Для внецентренно сжатых и растянутых элементов, находящихся под изгибом, момент рассчитывается для сечений, перпендикулярных их продольной оси.

Для элементов с сечениями в виде прямоугольника, квадрата или тавра применяются формулы, предельной нагрузки каждого элемента, для других сечений используются специальные нелинейные диаграммы.

Расчетное сопротивление позволит подобрать класс прочности и марку этого материала для получения оптимальных эксплуатационных свойств массива, элемента или детали. В отличие от нормативных показателей, данные учитывают геометрические особенности, условия эксплуатации, виды деформаций. Вводятся коэффициенты надежности по бетону, разновидности используемой арматуры и другие характеристики, влияющие на конечную прочность зданий и сооружений, где применяется литой бетон или конструктивные элементы из этого материла.

Источник