Расставьте в вершинах куба натуральные числа так что числа в соседних вершинах
Расставьте в вершинах куба натуральные числа так что числа в соседних вершинах
ъБДБЮБ 1. [ 3 ВБММБ ]
ч ЛЧБДТБФЕ 7*7 ЛМЕФПЛ ЪБЛТБУШФЕ ОЕЛПФПТЩЕ ЛМЕФЛЙ ФБЛ, ЮФПВЩ Ч ЛБЦДПК УФТПЛЕ Й Ч ЛБЦДПН УФПМВГЕ ПЛБЪБМПУШ ТПЧОП РП 3 ЪБЛТБЫЕООЩИ ЛМЕФЛЙ. [ 3 ВБММБ ]
уНПФТЙФЕ ТЕЫЕОЙЕ ЪБДБЮЙ N 2 Ч ЧБТЙБОФЕ 6 ЛМБУУБ.
ъБДБЮБ 2.
лБТМУПО ОБРЙУБМ ДТПВШ 10/97. нБМЩЫ НПЦЕФ:
1) РТЙВБЧМСФШ МАВПЕ ОБФХТБМШОПЕ ЮЙУМП Л ЮЙУМЙФЕМА Й ЪОБНЕОБФЕМА ПДОПЧТЕНЕООП,
2) ХНОПЦБФШ ЮЙУМЙФЕМШ Й ЪОБНЕОБФЕМШ ОБ ПДОП Й ФП ЦЕ ОБФХТБМШОПЕ ЮЙУМП.
уНПЦЕФ МЙ нБМЩЫ У РПНПЭША ЬФЙИ ДЕКУФЧЙК РПМХЮЙФШ ДТПВШ,
Б) ТБЧОХА 1/2? [ 2 ВБММБ ]
В) ТБЧОХА 1? [ 4 ВБММБ ]
тЕЫЕОЙЕ.
Б) дБ, ДПУФБФПЮОП РТЙВБЧЙФШ Л ЮЙУМЙФЕМА Й ЪОБНЕОБФЕМА РП 77. (л ЬФПНХ ЮЙУМХ РТЙЧПДЙФ ХТБЧОЕОЙЕ 2(10+x)=97+x.)
В) оЕФ. дЕКУФЧЙФЕМШОП, ДТПВШ ТБЧОБ ЕДЙОЙГЕ, ЕУМЙ ЕЕ ЮЙУМЙФЕМШ Й ЪОБНЕОБФЕМШ ТБЧОЩ. б нБМЩЫ ОЙЛБЛ ОЕ УНПЦЕФ ЙЪ ОЕТБЧОЩИ ЮЙУЕМ УДЕМБФШ ТБЧОЩЕ.
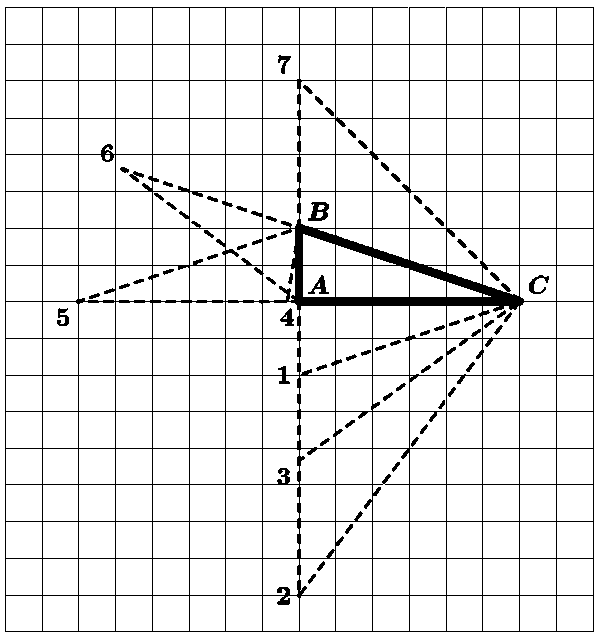
тЕЫЕОЙЕ.
оБ ТЙУХОЛЕ ГЙЖТБНЙ ПФНЕЮЕОЩ ЧЕТЫЙОЩ УЕНЙ РТЙМПЦЕООЩИ ФТЕХЗПМШОЙЛПЧ.
оБКДЙФЕ УБНЙ, ЛБЛЙЕ УФПТПОЩ РПМХЮБАФУС ТБЧОЩНЙ.
ъБДБЮБ 4. [ 8 ВБММПЧ ]
нПЦЕФ МЙ РТПЙЪЧЕДЕОЙЕ ДЧХИ РПУМЕДПЧБФЕМШОЩИ ОБФХТБМШОЩИ ЮЙУЕМ ТБЧОСФШУС РТПЙЪЧЕДЕОЙА ДЧХИ РПУМЕДПЧБФЕМШОЩИ ЮЈФОЩИ ЮЙУЕМ?
пФЧЕФ: оЕФ, ОЕ НПЦЕФ.
тЕЫЕОЙЕ. дПЛБЦЕН НЕФПДПН ПФ РТПФЙЧОПЗП.
рТЕДРПМПЦЙН, ЮФП ОБКДХФУС ДЧБ ОБФХТБМШОЩИ ЮЙУМБ k Й n ФБЛЙЕ, ЮФП n(n+1)=2k(2k+2). пФНЕФЙН ЮЙУМБ 2k Й 2k+2 ОБ ЮЙУМПЧПК ПУЙ Й ТБУУНПФТЙН ДЧБ УМХЮБС: n 2k Й n>2k.
еУМЙ n 2k, ФП n+1 2k, ФП n+1 > 2k+2, РПЬФПНХ n(n+1)>2k(2k+2). рТПФЙЧПТЕЮЙЕ.
ъБДБЮБ 5. [ 10 ВБММПЧ ]
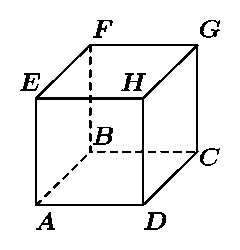
ч ЧЕТЫЙОБИ ЛХВБ ABCDEFGH ТБУУФБЧМЕОЩ ОБФХТБМШОЩЕ ЮЙУМБ ФБЛ, ЮФП ЮЙУМБ Ч УПУЕДОЙИ (РП ТЕВТХ) ЧЕТЫЙОБИ ПФМЙЮБАФУС ОЕ ВПМЕЕ ЮЕН ОБ ЕДЙОЙГХ. дПЛБЦЙФЕ, ЮФП ПВСЪБФЕМШОП ОБКДХФУС ДЧЕ ДЙБНЕФТБМШОП РТПФЙЧПРПМПЦОЩЕ ЧЕТЫЙОЩ, ЮЙУМБ Ч ЛПФПТЩИ ПФМЙЮБАФУС ОЕ ВПМЕЕ ЮЕН ОБ ЕДЙОЙГХ.
(рБТЩ ДЙБНЕФТБМШОП РТПФЙЧПРПМПЦОЩИ ЧЕТЫЙО ЛХВБ: A Й G, B Й H, C Й E, D Й F.)
тЕЫЕОЙЕ. пВПЪОБЮЙН ЮЙУМБ, УФПСЭЙЕ Ч ЧЕТЫЙОБИ ЛХВБ, УППФЧЕФУФЧХАЭЙНЙ НБМЕОШЛЙНЙ МБФЙОУЛЙНЙ ВХЛЧБНЙ: a, b, c, d, e, f, g Й h.
тБУУНПФТЙН ОБЙНЕОШЫЕЕ ЙЪ ЬФЙИ ЮЙУЕМ. вЕЪ ПЗТБОЙЮЕОЙС ПВЭОПУФЙ НЩ НПЦЕН УЮЙФБФШ, ЮФП ЬФП ЮЙУМП a (ПОП ОБИПДЙФУС Ч ЧЕТЫЙОЕ A). фПЗДБ ЮЙУМБ Ч УПУЕДОЙИ У A ЧЕТЫЙОБИ (ЬФП ЧЕТЫЙОЩ B, D Й E) НПЗХФ РТЙОЙНБФШ ФПМШЛП ЪОБЮЕОЙС a ЙМЙ a+1 (ФБЛ ЛБЛ a-1рХУФШ ТБЧОЩЕ ЮЙУМБ УФПСФ Ч ЧЕТЫЙОБИ B Й E (ПУФБМШОЩЕ УМХЮБЙ ТБУУНБФТЙЧБАФУС БОБМПЗЙЮОП). ч ЬФПН УМХЮБЕ ПФЧЕФПН ВХДХФ ДЙБНЕФТБМШОП РТПФЙЧПРПМПЦОЩЕ ЧЕТЫЙОЩ E Й C: e=b, Б ЮЙУМБ c Й b ПФМЙЮБАФУС ОЕ ВПМЕЕ, ЮЕН ОБ 1, РПЬФПНХ ЮЙУМБ e Й c ПФМЙЮБАФУС ОЕ ВПМЕЕ, ЮЕН ОБ 1.
бЧФПТЩ ЪБДБЮ:
б. а. нЙФСЗЙО (1), ч. ч. лМЕРГЩО (2), б. ыЕОШ (3), ч. ч. рТПЙЪЧПМПЧ (4), з. б. зБМШРЕТЙО (5)
Математический кружок 7 класс Подготовка к матпразднику
Решения занятия 19 Подготовка к матпразднику.
Задача 1. [4 балла] Каких прямоугольников с целыми сторонами больше: с периметром 2008 или с периметром 2009? (Прямоугольники a×b и b×a считаются одинаковыми.)
Решение. Прямоугольников с целыми сторонами и периметром 2009 вообще не существует, т. к. у прямоугольников с целыми сторонами периметр должен быть четным числом.

Задача 2. [5 баллов] Незнайка разрезал фигуру на трёхклеточные и четырёхклеточные уголки, нарисованные справа от неё. Сколько трёхклеточных уголков могло получиться?

Задача 3. [5 баллов] Дима живет в девятиэтажном доме. Он спускается на лифте со своего этажа на первый за 1 минуту. Из-за маленького роста Дима не достает до кнопки своего этажа. Поэтому, поднимаясь наверх, он нажимает ту кнопку, до которой может дотянуться, а дальше идет пешком. Весь путь наверх занимает 1 минуту 10 секунд. Лифт движется вверх и вниз с одинаковой скоростью, а Дима поднимается вдвое медленнее лифта. На каком этаже живет Дима?
Ответ. Дима живет на 7 этаже.
Решение. Из условия задачи видно, что хотя бы 1 этаж Диме пришлось подниматься пешком. Так как подъем занимает на 10сек. больше, и Дима поднимается в 2 раза медленнее лифта, то пешком Дима поднимается 20 секунд.
Пусть Дима поднимается пешком 1 этаж, тогда скорость лифта 1 этаж за 10сек., и за 1 минуту лифт преодолевает 6 этажей, т. е. Дима живет на 7 этаже (т. к. с первого этажа надо подняться на 6 этажей, т. е. оказаться на 7).
Задача 4. [6 баллов] Вовочка учится в спецшколе и получает оценки по 12-бальной системе. «Колов» там не ставят, а итоговую оценку в четверти выводят как среднее арифметическое текущих оценок, округляя в большую сторону. В конце четверти Вовочка выписал подряд в строчку свои текущие отметки по пению и поставил между некоторыми из них знак умножения. Произведение получившихся чисел оказалось равным 4018. Какая отметка выходит у Вовочки в четверти по пению? (Укажите все возможные варианты.)
Ответ. По пению у Вовочки вышло 6 в четверти.
Решение. Так как Вовочка получил число 4018 в результате произведения каких-нибудь целых чисел, то разложим число 4018 на простые множители, а затем соберем допустимые комбинации произведения.
4018=2*7*7*41 не подходит, так как оценки 41 нет, и нет 1, так же не подойдут и другие комбинации с множителем 41. Т. е. 41 должно быть обязательно сгруппировано с каким-то другим множителем.
Посмотрим всевозможные комбинации из трех множителей:
1) 4018=7*7*(2*41)=7*7*82 подходящая комбинация. Оценки получаются такими 2, 7, 7, 8. Средний балл: 
2) 4018=2*7*(7*41)=2*7*287 подходящая комбинация. Оценки получаются такими: 2, 2, 7, 7, 8. Средний балл: 
Посмотрим всевозможные комбинации из двух множителей:
1) 4018=(7*7)*(2*41)=49*82 подходящая комбинация. Оценки получаются такими 4, 9, 8, 2. Средний балл: 
2) 4018=(2*7)*(7*41)=14*287 – не подходит, т. к. ни оценки 14, ни 1 нет.
3) 4018=2*(7*7*41)=2*2009 явно не подходит, так же как и 4018, потому, что оценки 0 в Вовиной школе нет.
4) 4018=7*(7*2*41)=7*574 подходящая комбинация. Оценки получаются такими: 4, 5, 7, 7. Средний балл: 

Решение. Квадрат 4×4 имеет площадь равную 16, нам же нужен шестиугольник содержащая в себе все четыре вершины квадрата и с площадью 6. Поэтому достаточно из квадрата вырезать фигуру или фигуры общей площадью 10, так, чтобы добавилось два угла. Это можно сделать, вырезав 2 треугольника площадью 6 и 4 (смотри рисунок). Возможны и другие способы.

Доказательство. Рассмотрим всевозможные случаи для зафиксированной вершины и покажем, что во всех случаях найдется пара чисел, в диагонально противоположных вершинах, отличаются не более чем на 1.
Не нарушая общности, выберем произвольную вершину, например, F. Соседние с ней по ребру вершины – B, E, G. Среди чисел в этих четырех вершинах обязательно найдутся два одинаковых. Так как только 2 числа могут отличаться от данного на 1, а всего будет 3 числа.
Рассмотрим 2 случая:
1) Если среди чисел вершин B, E и G есть одинаковые числа. Пусть это будут числа в вершинах B и G. Тогда рассмотрим число в вершине G. Для G соседняя вершина H, в ней число, отличающееся от числа в G не более чем на 1. Вершины B и H диаметрально противоположные, так как число в B равно числу в G, следовательно, числа в B и H отличаются не более чем на 1.
2) Если среди чисел вершин B, E и G нет одинаковых, тогда какое-нибудь из чисел, например число в G, равно числу в F. Рассмотрим оставшиеся числа в E и B, они отличаются между собой на 2. Вершина A для вершин E и B является соседней, значит, число в вершине A будет равно числу в вершине F. А и G диагонально противоположные вершины, так как число в F равно числу в A и числу в G, то числа в A и G вообще не отличаются.
Расставьте в вершинах куба натуральные числа так что числа в соседних вершинах
Можно ли расставить в вершинах куба различные целые числа так, чтобы число в каждой вершине равнялось сумме трёх чисел на концах рёбер, выходящих из этой вершины?
Обозначим вершины куба, как обычно, через ABCDA1B1C1D1, вершины А, С, B1 и D1 назовём чёрными, вершины B, D, A1, C1 — белыми. Один конец каждого ребра при этом белый, второй — чёрный, для каждой вершины все соседние имеют противоположный цвет. Каждое число равно сумме трёх соседних чисел противоположного цвета и каждое число один раз участвует в суммах для трёх соседних чисел противоположного цвета. Следовательно, сумма всех белых чисел равна утроенной сумме всех чёрных чисел и наоборот, откуда сумма всех чёрных чисел и сумма всех белых чисел равны нулю. Значит, число в вершине А равно сумме чисел в вершинах B, D и A1, а она равны числу в вершине С1 с обратным знаком. Таким образом, в концах каждой большой диагонали куба записаны противоположные числа. Следовательно, если задать три числа в вершинах B, D и A1, они полностью определят все оставшиеся числа требуемым в задаче образом. Задав их как 1, 2, 3, получим один из ответов задачи.
Ответ: Да, можно, например: в вершинах нижней грани по часовой стрелке 6, 1, −3, 2, в вершинах верхней грани над ними: 3, −2, −6, −1.
Расставьте в вершинах куба натуральные числа так что числа в соседних вершинах
а) Можно ли занумеровать рёбра куба натуральными числами от 1 до 12 так, чтобы для каждой вершины куба сумма номеров рёбер, которые в ней сходятся, была одинаковой?
б) Аналогичный вопрос, если расставлять по рёбрам куба числа –6, –5, –4, –3, –2, –1, 1, 2, 3, 4, 5, 6.
а) Сложим числа вокруг каждой вершины и потом сложим все 8 сумм. С одной стороны, каждое число на ребре посчитано два раза, поэтому сумма равна с другой стороны, она равна 8x, где x — сумма чисел на ребрах вокруг одной вершины. Но 156 не делится на 8.
б) Пусть вершины куба названы Поставим на ребрах числа так:
Тогда суммы вокруг всех вершин равны 0.