Равновеликие фигуры что это

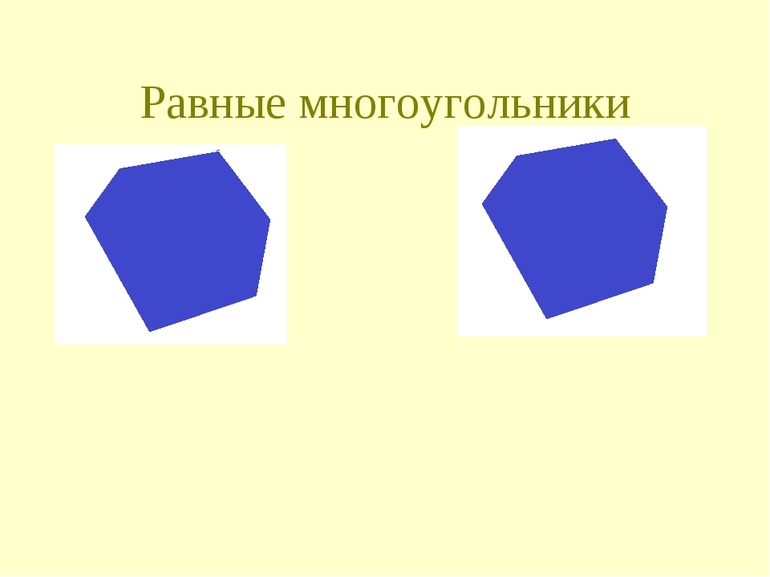
Равные многоугольники

По определению равные фигуры должны быть во всём одинаковыми, включая площадь, длину сторон, размер углов и другие параметры. Чтобы рассмотреть всё из них, уйдёт много времени, да это и не нужно, ведь они взаимозависимы. Хорошим примером будет самый простой многоугольник — треугольник. Существует несколько правил, по которым можно определить, равны ли 2 треугольника между собой или нет:

Нельзя путать первое условие с тремя углами. Ведь если в треугольнике равны 3 угла, они необязательно будут равными, но будут подобными.

Названия условий достаточно точно описывают критерии, по которым можно определить одинаковые 2 треугольника или нет. Из них следует, что необязательно знать все параметры: часто хватает только нескольких из них для определения «равности».

В большинстве случаев определить одинаковость других фигур гораздо сложнее, нежели треугольников. К счастью, чаще всего в школьной геометрии такой класс задач не рассматривают или даются дополнительные данные, помогающие с решением.

Например, доказательство «равности» для четырёхугольника сложнее, да и почти не встречается. Но если по условию сказано, что четырёхугольник не произвольный, а имеет прямые углы, задача становится проще. В таком случае рассматривается прямоугольник. А для него достаточно, чтобы 2 не противолежащие стороны были равны.

Если указано ещё и условие, что прямоугольник является квадратом, достаточно указать, что у двух таких фигур совпадает по длине одна сторона и уже этого будет достаточно.

Равность правильных фигур

Частным и самым простым для сравнения является случай, когда многоугольник по условию правильный. Так называется фигура с одинаковыми сторонами и углами. Например, равносторонний треугольник и квадрат. Важно не забывать проверить равны ли углы, так как не каждая фигура правильная. Тот же ромб по определению имеет 4 совпадающие по длине стороны, но разные углы. При сравнении правильных многоугольников достаточно указать, что, хотя бы одна сторона фигуры равна стороне у другой. Это будет достаточное условие для доказательства «равности».

Самым простым и наглядным способом сверки двух фигур будет не геометрический с помощью правил, а путём наложения рисунков друг на друга. Разумеется, что он не претендует на точность, но изобразить параллелограмм и наложить его на другой нагляднее, чем сравнивать, например, углы. Понятно, что так можно только ознакомиться с концепцией «равности» и показать, какие фигуры называются равными, для упрощения в дальнейшем решения задач, но доказывать что-либо нельзя, ввиду неточности метода.

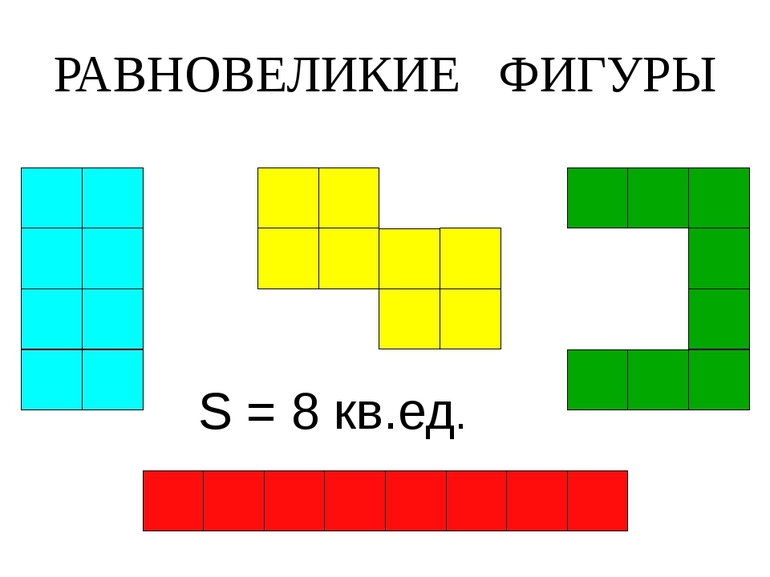
Если при сравнении двух тел оказывается, что их площади равны, такие тела (многоугольники) являются равновеликими. Как и в случае с прошлым, это определение звучит несложно. Проблемы могут начаться непосредственно при вычислении площадей. Самый простой многоугольник — треугольник. Для вычисления его площади существует множество способов.

Вычисление площади треугольника

Чаще всего приходится работать с прямоугольными треугольниками. Их площадь вычислить несложно — это полупроизведение катетов (сторон, между которыми лежит прямой угол). Таким образом, даже если стороны двух фигур по длине разные, но их произведение равно, они равновеликие. Например, треугольник с катетами 4 и 4 равен по площади многоугольнику с катетами 16 и 1. Так как их полупроизведение, а значит и площадь равна 8.

Если же треугольник произвольный (то есть не является частным случаем — прямоугольным, равнобедренным или равносторонним), можно воспользоваться одной из 5 формул, позволяющих вычислить его площадь.

То, какую формулу использовать, будет зависеть от данных, предоставленных в задаче. Иногда придётся проводить дополнительное построение, например, провести высоту или использовать свойства, что биссектрисы пересекаются в центре вписанной окружности. Если не даны все 3 стороны, использовать третью формулу не получится.

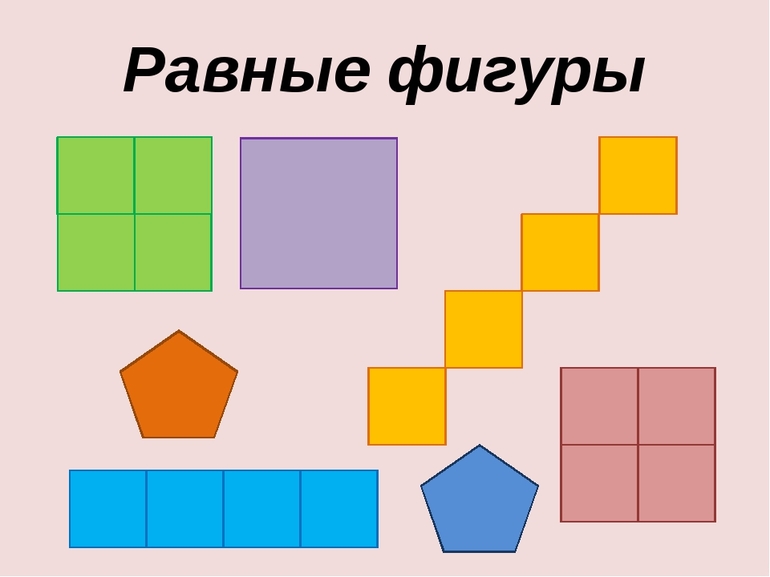
Важно понять, что фигуры могут быть разными по количеству углов, но всё равно считаться равновеликими — в учёт идёт только площадь, остальные параметры не важны. Например, прямоугольный треугольник с катетами 2 и 4 будет визуально казаться больше, чем квадрат со стороной 2, но их площади совпадают и равны 4 (площадь прямоугольника считается как произведение прилежащих сторон друг на друга). По определению это делает их равновеликими.

Визуальный способ

Существует также наглядный, но неточный способ. Нужно взять листок в клеточку и нарисовать на нём многоугольники. Если рисунок получился большой — не страшно, так будет только проще в дальнейшем. Следующий шаг — посчитать количество клеток, которое заняла каждая фигура и сравнить. Если оно равно, равновеликость доказана. Опять же метод не точный, но для введения в концепцию площадей и их «равности» подойдёт.

Иногда встречается словосочетание «равносоставленная фигура». Такими называют произвольные многоугольники, которые можно составить друг из друга путём разрезания одного из них на одинаковые объекты и перекладывания. Например, если прямоугольник 4 на 1 нарезать на одинаковые части — квадраты 1 на 1, то из полученных маленьких квадратов можно составить один большой со стороной 2. Но это не более чем забавное свойство некоторых фигур и в геометрии фактически почти не используется.

Источник

Равновеликие фигуры — свойства, формулы и примеры

При рассмотрении и сравнении фигур в геометрии часто применяют определения «равные» и «равновеликие» фигуры. На первый взгляд может показаться, что это слова-синонимы, но это неверно. Для начала стоит определить, какие фигуры называют равными — так можно назвать только 2 полностью идентичных многоугольника. Равновеликими считаются тела, площади или объёмы которых совпадают, в то время как остальные параметры могут различаться.

Равные многоугольники

По определению равные фигуры должны быть во всём одинаковыми, включая площадь, длину сторон, размер углов и другие параметры. Чтобы рассмотреть всё из них, уйдёт много времени, да это и не нужно, ведь они взаимозависимы. Хорошим примером будет самый простой многоугольник — треугольник. Существует несколько правил, по которым можно определить, равны ли 2 треугольника между собой или нет:

Нельзя путать первое условие с тремя углами. Ведь если в треугольнике равны 3 угла, они необязательно будут равными, но будут подобными.

Названия условий достаточно точно описывают критерии, по которым можно определить одинаковые 2 треугольника или нет. Из них следует, что необязательно знать все параметры: часто хватает только нескольких из них для определения «равности».

В большинстве случаев определить одинаковость других фигур гораздо сложнее, нежели треугольников. К счастью, чаще всего в школьной геометрии такой класс задач не рассматривают или даются дополнительные данные, помогающие с решением.

Например, доказательство «равности» для четырёхугольника сложнее, да и почти не встречается. Но если по условию сказано, что четырёхугольник не произвольный, а имеет прямые углы, задача становится проще. В таком случае рассматривается прямоугольник. А для него достаточно, чтобы 2 не противолежащие стороны были равны.

Если указано ещё и условие, что прямоугольник является квадратом, достаточно указать, что у двух таких фигур совпадает по длине одна сторона и уже этого будет достаточно.

Равность правильных фигур

Частным и самым простым для сравнения является случай, когда многоугольник по условию правильный. Так называется фигура с одинаковыми сторонами и углами. Например, равносторонний треугольник и квадрат. Важно не забывать проверить равны ли углы, так как не каждая фигура правильная. Тот же ромб по определению имеет 4 совпадающие по длине стороны, но разные углы. При сравнении правильных многоугольников достаточно указать, что, хотя бы одна сторона фигуры равна стороне у другой. Это будет достаточное условие для доказательства «равности».

Самым простым и наглядным способом сверки двух фигур будет не геометрический с помощью правил, а путём наложения рисунков друг на друга. Разумеется, что он не претендует на точность, но изобразить параллелограмм и наложить его на другой нагляднее, чем сравнивать, например, углы. Понятно, что так можно только ознакомиться с концепцией «равности» и показать, какие фигуры называются равными, для упрощения в дальнейшем решения задач, но доказывать что-либо нельзя, ввиду неточности метода.

Если при сравнении двух тел оказывается, что их площади равны, такие тела (многоугольники) являются равновеликими. Как и в случае с прошлым, это определение звучит несложно. Проблемы могут начаться непосредственно при вычислении площадей. Самый простой многоугольник — треугольник. Для вычисления его площади существует множество способов.

Вычисление площади треугольника

Чаще всего приходится работать с прямоугольными треугольниками. Их площадь вычислить несложно — это полупроизведение катетов (сторон, между которыми лежит прямой угол). Таким образом, даже если стороны двух фигур по длине разные, но их произведение равно, они равновеликие. Например, треугольник с катетами 4 и 4 равен по площади многоугольнику с катетами 16 и 1. Так как их полупроизведение, а значит и площадь равна 8.

Если же треугольник произвольный (то есть не является частным случаем — прямоугольным, равнобедренным или равносторонним), можно воспользоваться одной из 5 формул, позволяющих вычислить его площадь.

То, какую формулу использовать, будет зависеть от данных, предоставленных в задаче. Иногда придётся проводить дополнительное построение, например, провести высоту или использовать свойства, что биссектрисы пересекаются в центре вписанной окружности. Если не даны все 3 стороны, использовать третью формулу не получится.

Важно понять, что фигуры могут быть разными по количеству углов, но всё равно считаться равновеликими — в учёт идёт только площадь, остальные параметры не важны. Например, прямоугольный треугольник с катетами 2 и 4 будет визуально казаться больше, чем квадрат со стороной 2, но их площади совпадают и равны 4 (площадь прямоугольника считается как произведение прилежащих сторон друг на друга). По определению это делает их равновеликими.

Визуальный способ

Существует также наглядный, но неточный способ. Нужно взять листок в клеточку и нарисовать на нём многоугольники. Если рисунок получился большой — не страшно, так будет только проще в дальнейшем. Следующий шаг — посчитать количество клеток, которое заняла каждая фигура и сравнить. Если оно равно, равновеликость доказана. Опять же метод не точный, но для введения в концепцию площадей и их «равности» подойдёт.

Иногда встречается словосочетание «равносоставленная фигура». Такими называют произвольные многоугольники, которые можно составить друг из друга путём разрезания одного из них на одинаковые объекты и перекладывания. Например, если прямоугольник 4 на 1 нарезать на одинаковые части — квадраты 1 на 1, то из полученных маленьких квадратов можно составить один большой со стороной 2. Но это не более чем забавное свойство некоторых фигур и в геометрии фактически почти не используется.

Источник

Инструменты пользователя

Инструменты сайта

Боковая панель

Навигация

Загрузки всякие

Связь

Содержание

Площадь. Равновеликие фигуры

Разрезанием на части и перекладыванием их можно любой многоугольник превратить в равновеликий ему квадрат.

Понятие равносоставленности лежит в основе «метода разбиения», применяемого для вычисления площадей многоугольников: параллелограмм «разрезанием и перекладыванием» сводят к прямоугольнику, треугольник — к параллелограмму, трапецию — к треугольнику.

Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.

Достроим треугольник до прямоугольника. Площадь треугольника равна половине площади прямоугольника.

Проведем через середину боковой стороны трапеции прямую, параллельную второй боковой стороне. Площадь трапеции равна площади полученного параллелограмма.

Перекраивание трапеции в равносоставленный треугольник:

Пло­щадь тра­пе­ции с ос­но­ва­ни­я­ми длин a и b и дли­ной вы­со­ты h рав­на S=(a+b)/2•h. Убе­дить­ся в этом мож­но вос­поль­зо­вав­шись фор­му­лой для вы­чис­ле­ния пло­ща­ди тре­уголь­ни­ка. Для это­го необ­хо­ди­мо разре­зать тра­пе­цию на та­кие ча­сти, из ко­то­рых мож­но со­ста­вить треугольник.

Разре­жем тра­пе­цию вдоль ли­нии, со­еди­ня­ю­щей вер­ши­ну с се­ре­ди­ной проти­во­по­лож­ной бо­ко­вой сто­ро­ны. По­вер­нём от­ре­зан­ный тре­уголь­ник до того момен­та, ко­гда оба ос­но­ва­ния тра­пе­ции ока­жут­ся на од­ной прямой. Убедитесь, что две ча­сти бо­ко­вой сто­ро­ны при этом ля­гут на од­ну прямую, то есть, получится дей­стви­тель­но тре­уголь­ник.

Одна из сторон получив­ше­го­ся тре­уголь­ни­ка име­ет дли­ну, рав­ную сум­ме длин оснований трапе­ции, а дли­на вы­со­ты тре­уголь­ни­ка, про­ве­дён­ной к этой стороне, сов­пада­ет с вы­со­той тра­пе­ции.

Один из способов подсчё­та пло­ща­ди тре­уголь­ни­ка со­сто­ит в на­хож­де­нии половины произве­дения дли­ны сто­ро­ны на дли­ну вы­со­ты, опу­щен­ную на эту сторону. При­ме­нение это­го спо­со­ба и да­ёт при­выч­ную фор­му­лу площа­ди трапеции.

Модель мож­но сде­лать из доски толщиной около 10 мм. Для удобства демон­стра­ции две ча­сти, на которые она разрезает­ся, удобно со­еди­нять между собой при по­мо­щи маг­ни­тов.

Равносоставленность

Равновеликие многогранники не всегда являются равносоставленными. Так, например, куб и равновеликий ему правильный тетраэдр не являются равносоставленными — так называемая теорема Дена.

Источник

Равновеликие фигуры

Пло́щадь фигуры — числовая характеристика фигуры. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.

Содержание

Об определении

Формальное введение понятия площадь и объём можно найти в статье мера Жордана, здесь мы приводим лишь намётки определения с комментариями.

Площадь — это вещественнозначная функция, определённая на определённом классе фигур евклидовой плоскости, такая что:

Определённый класс должен быть замкнут относительно пересечения и объединения, а также относительно движений плоскости и включать в себя все многоугольники. Из этих аксиом следует монотонность площади, то есть

Связанные определения

Комментарии

На самом деле, есть довольно неестественный и неоднозначный способ определить площадь для всех ограниченных подмножеств плоскости. На множестве всех ограниченных подмножеств плоскости существуют различные функции площади, т. е. не равные функции, удовлетворяющие вышеприведённым аксиомам, а множество квадрируемых фигур является максимальным множеством фигур на которых функционал площади определяется однозначно.

То же самое можно сделать для длины на прямой, но нельзя для объёма в евклидовом пространстве и также нельзя для площади на единичной сфере в евклидовом пространстве, (смотри соответственно парадокс Банаха — Тарского и парадокс Хаусдорфа).

Площади некоторых фигур

Площадь прямоугольника со сторонами а и b равна произведению их сторон: S = ab.

Площадь произвольного четырехугольника равна половине произведения диагоналей и синуса угла между ними.

Площадь треугольника равна половине произведения основания, умноженного на высоту.

См. также

Ссылки

Полезное

Смотреть что такое «Равновеликие фигуры» в других словарях:

РАВНОВЕЛИКИЕ ФИГУРЫ — плоские фигуры с одинаковыми площадями или геометрические тела с одинаковыми объемами … Большой Энциклопедический словарь

равновеликие фигуры — плоские фигуры с одинаковыми площадями или геометрического тела с одинаковыми объёмами. * * * РАВНОВЕЛИКИЕ ФИГУРЫ РАВНОВЕЛИКИЕ ФИГУРЫ, плоские фигуры с одинаковыми площадями или геометрические тела с одинаковыми объемами … Энциклопедический словарь

РАВНОВЕЛИКИЕ ФИГУРЫ — плоские фигуры с одинаковыми площадями или геом. тела с одинаковыми объёмами … Естествознание. Энциклопедический словарь

Равновеликие и равносоставленные фигуры — Равновеликие фигуры плоские (пространственные) фигуры одинаковой площади (объёма); равносоставленные фигуры фигуры, которые можно разрезать на одинаковое число соответственно конгруэнтных (равных) частей. Обычно понятие… … Большая советская энциклопедия

РАВНОВЕЛИКИЙ — РАВНОВЕЛИКИЙ, ая, ое; ик. 1. Равный по силе, возможностям, значению (книжн.). Равновеликие явления. 2. равновеликие фигуры (тела) в математике: фигуры (тела), равные по площади или объёму. | сущ. равновеликость, и, жен. Толковый словарь Ожегова.… … Толковый словарь Ожегова

Словарь терминов планиметрии — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия

Коллинеарные точки — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Конкурентные прямые — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Окружность Аполония — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Источник

РАВНОВЕЛИКИЕ ФИГУРЫ

Смотреть что такое «РАВНОВЕЛИКИЕ ФИГУРЫ» в других словарях:

равновеликие фигуры — плоские фигуры с одинаковыми площадями или геометрического тела с одинаковыми объёмами. * * * РАВНОВЕЛИКИЕ ФИГУРЫ РАВНОВЕЛИКИЕ ФИГУРЫ, плоские фигуры с одинаковыми площадями или геометрические тела с одинаковыми объемами … Энциклопедический словарь

Равновеликие фигуры — Площадь фигуры числовая характеристика фигуры. В простейшем случае, когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов. Содержание 1 Об определении 2 Связанные определения 3 Комментарии … Википедия

РАВНОВЕЛИКИЕ ФИГУРЫ — плоские фигуры с одинаковыми площадями или геом. тела с одинаковыми объёмами … Естествознание. Энциклопедический словарь

Равновеликие и равносоставленные фигуры — Равновеликие фигуры плоские (пространственные) фигуры одинаковой площади (объёма); равносоставленные фигуры фигуры, которые можно разрезать на одинаковое число соответственно конгруэнтных (равных) частей. Обычно понятие… … Большая советская энциклопедия

РАВНОВЕЛИКИЙ — РАВНОВЕЛИКИЙ, ая, ое; ик. 1. Равный по силе, возможностям, значению (книжн.). Равновеликие явления. 2. равновеликие фигуры (тела) в математике: фигуры (тела), равные по площади или объёму. | сущ. равновеликость, и, жен. Толковый словарь Ожегова.… … Толковый словарь Ожегова

Словарь терминов планиметрии — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия

Коллинеарные точки — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Конкурентные прямые — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Окружность Аполония — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия

Источник