Равные площади треугольников что дают
Как найти площадь треугольника
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
3. Площадь треугольника через описанную окружность и стороны
4. Площадь треугольника через вписанную окружность и стороны
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
Площадь прямоугольного треугольника по формуле Герона
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
Равные площади треугольников что дают
§2. Площадь треугольника. Метод площадей
В школьном курсе геометрии доказано несколько формул площади треугольника. Напомним их.
При вычислении площади из этих формул следует выбрать ту, которая в условиях конкретной задачи приводит к более простому решению.
Для примера, рассмотрим два треугольника:
`DeltaABC:` `AB=13`, `BC=14`, `AC=15`;
`DeltaKML:` `KL=sqrt(13)`, `LM=sqrt(14)`, `KM=sqrt(15)`;
Надо найти площадь и радиус описанной окружности.
Для треугольника `ABC` удобен ход решения такой:
`p=1/2(AB+BC+AC)=21`, по формуле Герона
`S_(ABC)=sqrt(21*6*7*8)= ul(84)` и по формуле (5)
тогда `sinM=sqrt(1-64/(210))=(sqrt(146))/(sqrt(14)*sqrt(15))` и по формуле (2):
тогда `R=(KL)/(2sinM)=ul((sqrt(13)*sqrt(14)*sqrt(15))/(2*sqrt(146)))=(sqrt(13)*sqrt7*sqrt(15))/(2*sqrt(73))` (точно также по формуле 5).
Сравнение площадей треугольников обычно опирается на одно из следующих утверждений:
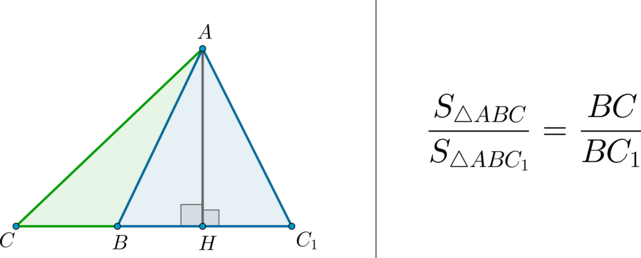
$$ 2.<1>^<○>$$. Площади треугольников с одинаковой высотой относятся как длины соответствующих оснований. В частности, если точка `D` лежит на основании `AC` (рис. 6а), то
$$ 2.<2>^<○>$$. Площади треугольников с общим углом относятся как произведения сторон, заключающих этот угол (см. рис. 6б):
$$ 2.<3>^<○>$$. Площади подобных треугольников относятся как квадраты их
сходственных сторон, т. е. если `Delta ABC
DeltaA_1B_1C_1`, то `(S_(A_1B_1C_1))/(S_(ABC))=((A_1B_1)/(AB))^2`.
Все эти утверждения легко доказываются с использованием соответственно формул площади (1) и (2).
Обратим внимание на важное свойство медиан треугольника.
Три медианы треугольника разбивают его на `6` треугольников с общей вершиной и равными площадями.
Докажем, например, для треугольника `BOM`, что `S_(BOM)=1/6S_(ABC)`.
Дан треугольник `ABC`. Точка `D` лежит на стороне `AB`, `AD:DB=1:2`, точка `K` лежит на стороне `BC`, `BK:KC=3:2` (рис. 8а). Отрезки `AK` и `CD` пересекаются в точке `O`. Найти отношение площади четырёхугольника `DBKO` к площади треугольника `ABC`.
2. Через точку `D` проведём прямую `DL«|\|«AK`. По теореме о пересечении сторон угла параллельными прямыми (`/_ABC`, `DL«|\|«AK`) имеем `(BL)/(LK)=(BD)/(AD)`, откуда `LK=y`.
По той же теореме (`/_DCB`, `OK«|\|«DL`) получим `(DO)/(DC)=(LK)/(LC)`, `DO=1/3DC`.
3. Теперь находим `S_(ADO):S_(ADC)=DO:DC`, `a=1/3(1/3S)=1/9S`.
(Можно по теореме Менелая для треугольника `BCD` и секущей `CD:`
`(BK)/(KC)*(CO)/(OD)*(DA)/(AB)=1 iff 3/2*(CO)/(OD)*1/3=1 iff CO=2OD=>OD=1/3DC`).
Находим площадь: `sigma=3/5S-a=(3/5-1/9)S=22/45S`.
Найти площадь треугольника, две стороны которого равны `3` и `7`, а медиана к третьей стороне равна `4` (рис. 9).
Пусть `AB=3`, `BC=7`, `AM=MC` и `BM=4`. Достроим треугольник `ABC` до параллелограмма, для этого на прямой `BM` отложим отрезок `MD=BM` и соединим точки: `A` с `D` и `C` с `D`. Противоположные стороны параллелограмма равны: `(DC=AB)` и равны площади треугольников `ABC` и `DBC` (общее основание `BC` и равные высоты из вершин `A` и `D`).
В треугольнике `DBC` известны все три стороны: `BC=7`, `DC=3`, `BD=2BM=8`.
Находим его площадь по формуле Герона: `p=9`, `S_(BCD)=6sqrt3`.
Значит и `S_(ABC)=6sqrt3`.
В решении этой задачи дополнительным построением получен треугольник, площадь которого равна площади заданного и легко вычисляется по данным задачи. Приведём ещё одну задачу, где сначала вычисляется площадь дополнительно построенной фигуры, а затем легко находится искомая площадь.
Найти площадь треугольника, если его медианы равны `3`, `4` и `5`.
По свойству медиан `AO=2/3m_a`, `CO=2/3m_c` и `ON=1/3m_b`. В треугольнике `AOC` известны две стороны `AO` и `CO` и медиана третьей стороны `ON`. Площадь этого треугольника найдём как в предыдущей задаче.
Достроим треугольник `AOC` до параллелограмма `AOCD`, `S_(AOC)=S_(DOC)`, в треугольнике `DOC` известны три стороны:
`DO=2ON=2/3m_b`, `OC=2/3m_c`, `DC=AO=2/3m_a`.
Площадь треугольника `DOC` вычисляем по формуле Герона `S_1=S_(AOC)=S_(DOC)=8/3`. Сравним теперь площадь треугольника `ABC` (обозначим её `S`) с площадью треугольника `AOC`. Из теоремы 2 о медианах и площадях следует `S_(AOC)=S_(AON)+S_(NOC)=2*1/6S=1/3S`.
В следующей задаче докажем лемму об отношении площади треугольника к площади другого треугольника, построенного из медиан первого.
Найти отношение площади `S` треугольника к площади `S_0` треугольника, составленного из медиан первого.
Рассмотрим рис. 10. В построенном треугольнике `OCD` стороны таковы: `OC=2/3m_c`, `OD=2/3m_b`, `CD=2/3m_a`. Очевидно, что треугольник со сторонами `m_a`, `m_b`, `m_c` подобен (по третьему признаку) треугольнику со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`.
| `S_(m_am_bm_c)=3/4S_(abc)`. |
Около окружности радиуса `sqrt3` описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки `9` и `5`.
Пусть `AP=9`, `PC=5` (рис. 11) и пусть `BM=x`. По свойству касательных `AM=AP`, `CN=CP` и `BN=BM`, поэтому стороны треугольника таковы: `AC=14`, `AB=9+x`, `BC=5+x`, тогда `p=14+x`. (Заметим, что `p=AC+BM`!). По формулам площади (3) и (4) имеем: `S=pr=(14+x)sqrt3` и `S=sqrt((14+x)x*5*9)`. Приравниваем правые части, возводим в квадрат, приводим подобные члены, получаем `x=1`. Вычисляем площадь треугольника:
Приём, применённый в решении этой задачи, когда площадь фигуры выражается двумя различными способами, часто используется в задачах на доказательство.
Проведём два примера, в каждом выведем полезную формулу.
В треугольнике `ABC` угол `C` равен `varphi`, `AC=b`, `BC=a` (рис. 12). Доказать, что биссектриса `CD` равна `(2ab)/(a+b) cos varphi/2`.
Обозначим `CD=x`. Очевидно, что `S_(ABC)=S_(ACD)+S_(DCB)`. По формуле (2) `S_(ABC)=1/2 ab sin varphi`, `S_(ACD)=1/2 bx sin varphi/2`, `S_(BDC)=1/2 ax sin varphi/2`. Таким образом, имеем: `1/2 ab sin varphi=1/2(a+b)x sin varphi/2`. Используем формулу синуса двойного угла `sin varphi=2sin varphi/2 cos varphi/2`, получим:
называется окружность, касающаяся одной из сторон треугольника и продолжений двух других сторон. Таких окружностей, очевидно, три (рис. 13). Их радиусы обычно обозначаются `r_a`, `r_b`, `r_c` в зависимости от того, какой стороны окружность касается.
Вневписанная окружность касается стороны `a=BC` треугольника `ABC` (рис. 14). Доказать, что `S_(ABC)=r_a(p-a)`, где `2p=a+b+c`.
Считаем площадь `S_0` четырёхугольника `ABI_aC`:
`S_0=S_(ABC)+S_(BCI_a)` и `S_0=S_(ABI_a)+S_(ACI_a)`, откуда
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
Если известны длины трех сторон
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
Основные свойства площадей треугольников
Факт 1.
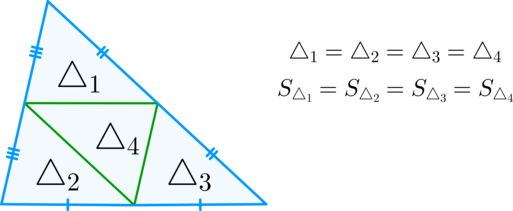
\(\bullet\) Средние линии треугольника разбивают его на 4 равных треугольника.
Соответственно, площади этих треугольников равны.
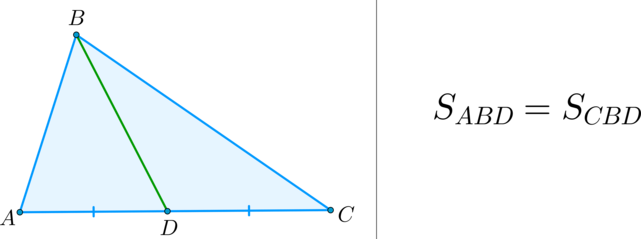
Факт 2.
\(\bullet\) Медиана треугольника делит его на два треугольника, равных по площади (равновеликих).
Факт 3.
\(\bullet\) Все 3 медианы треугольника делят его на 6 равновеликих треугольников.
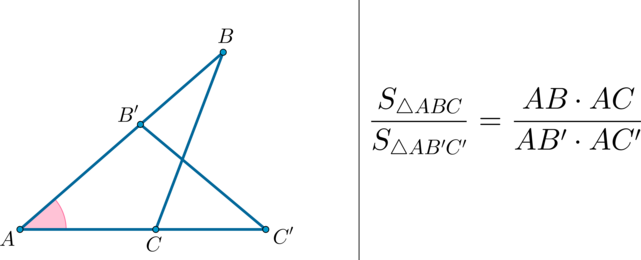
Факт 4.
\(\bullet\) Площади треугольников, имеющих одинаковый угол, относятся как произведения сторон, образующих этот угол.
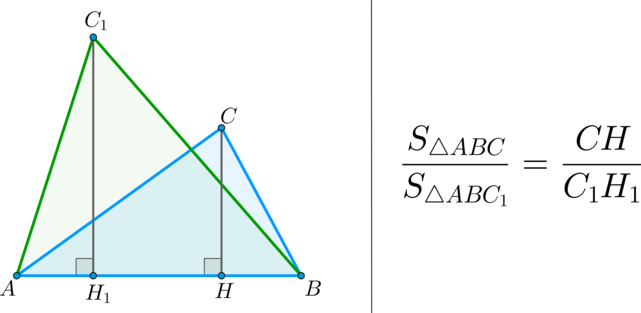
Факт 5.
\(\bullet\) Площади треугольников, имеющих одинаковое основание, относятся как высоты, проведенные к этим основаниям.
Факт 6.
\(\bullet\) Площади треугольников, имеющих одинаковую высоту, относятся как основания, к которым проведена эта высота.
Факт 7.
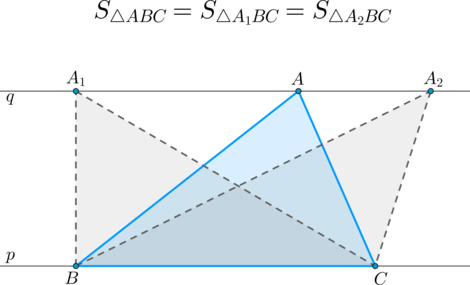
\(\bullet\) Если прямые \(p\) и \(q\) параллельны, то
Факт 8.
\(\bullet\) Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
\(\bullet\) Отношение периметров подобных треугольников равно коэффициенту подобия.
Площадь треугольника
Определение площади треугольника
Площадь треугольника — это величина, которая
показывает какие размеры у треугольника.
Сейчас, на примере покажем, что такое площадь,
а также, как можно найти площадь треугольника.
Площадь треугольника, можно очень легко объяснить
на примере прямоугольного треугольника в клеточном поле.
Площадь, в нашем случае, будет равна количеству клеток.
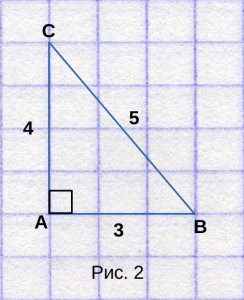
Для наглядности, нарисуем прямоугольный треугольник
ABC, со длинами сторон 3, 4 и 5, как на рисунке 2. Отметим, что он прямоугольный.
Посчитаем количество клеток, которые занимает треугольник.
3 полных клетки, и 4 неполных клетки, но для того, чтобы узнать
площадь треугольника в клеточном поле нам нужно узнать количество
полных клеток, которые занимает весь треугольник. Наша задача в том,
чтобы неполные клетки преобразовать в полные.
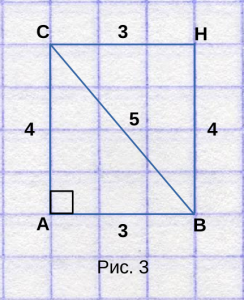
Для этого нарисуем второй треугольник, так,
чтобы получился прямоугольник, как на рисунке 3.
Как видим, весь прямоугольник занимает 12 полных клеток.
Формула площади прямоугольника равна произведению
одной стороны на другую — \( S = ab \) ,
поэтому площадь прямоугольника равна 3 * 4 = 12 клеткам.
Площадь треугольника, из которого состоит прямоугольник,
можно найти по другой формуле: \( S = \frac<1>2 ab \) .
Подставив значения длин сторон, получаем — S = 0.5 * 3 * 4,
из чего следует, что S = 6 клетками, или же квадратным сантиметрам.
Прямоугольник можно условно разделить
на два треугольника, поэтому площадь треугольника
равна половине площади прямоугольника.
Формула площади треугольника — это формула,
по которой можно найти площадь треугольника.
Формулы площади треугольника применяют, только,
и только тогда, когда невозможно узнать площадь
треугольника, глядя на рисунок, или просто посчитав клетки.
Формулы площади треугольника
Ⅰ. Через высоту и основание
a — сторона, на которую падает высота,
b — высота.
Самая известная формула площади треугольника.
Зная только высоту и сторону, на которую падает
эта высота, можно найти площадь треугольника.
Ⅱ. Через все стороны и периметр
p — полупериметр, вычисляется по формуле: \( p = \frac
a, b, c — стороны треугольника.
Это формулу, нужно использовать когда известны
все три стороны треугольника. Зная три стороны
треугольника можно найти периметр, а дальше
найти и площадь заданного треугольника.
Эту формулу площади также называют формулой Герона.
Ⅲ. Через две стороны и угол между ними
\[ S = \frac<1> <2>a \cdot b \cdot \sin β \]
a, b — стороны между которыми расположен угол β,
sin β — синус угла β.
Формула применяется, когда известен
один из углов, и две стороны, образующие
этот угол. В некоторых задачах площадь
треугольника можно найти только по этой формуле.
Ⅳ. Через периметр и радиус вписанной окружности
r — радиус вписанной окружности,
P — периметр треугольника.
Тут даже не обязательно знать все стороны треугольника,
достаточно знать периметр и радиус описанной окружности.
Ⅴ. Через все стороны и радиус описанной окружности
abc — произведение всех сторон треугольника,
R — радиус описанной окружности.
Пожалуй, единственная формула, где площадь
треугольника можно найти только через радиус
описанной окружности и произведение трех сторон.
Ⅵ. Через сторону и два прилежащих к ней угла
a — сторона треугольника,
sin α — синус угла α,
sin β — синус угла β.
Готов поспорить, вы даже ни разу не видели этой формулы.
Эта очередная формула площади треугольника, применяется
в крайне редких случаях — когда известны два угла и сторона,
к которой эти углы примыкают.