Размерность и единица измерения в чем разница
Научная электронная библиотека
8.5.1 Единицы измерения, размерность
Прежде чем приступить к рассмотрению методики определения критериев подобия на основе анализа размерностей, кратко сформулируем необходимые исходные определения.
1. Единицей измерения [А] физической величины А является условно выбранная физическая величина а, имеющая тот же физический смысл, что и величина А. Измерение физической величины А сводится к сравнению ее с некоторой одноименной величиной а, принятой за единицу.
В качестве стандарта принят ГОСТ 8.417 – 81 «Единицы физических величин», основу которой составляет Международная система единиц СИ.
2. Различают основные единицы измерения – независимо установленные единицы измерения для произвольно выбранных физических величин и производные единицы измерения.
Производные единицы измерения отражают функциональную взаимосвязь между основными единицами измерения на основе физических законов.
Размерность любой физической величины представляет собой произведение возведенных в степени размерностей основных единиц измерения.
4. Различают параметры с независимыми размерностями (независимые параметры) и параметры с зависимыми размерностями (зависимые параметры). Группа независимых параметров – это такая группа параметров, в которой размерность ни одного из параметров не может быть образована из размерностей других параметров, при надлежащей той же группе. Примером группы независимых параметров могут служить группы (l, m, υ) и (m, υ,a), так как
Параметры групп ( Ђ,Ј,V )я(ГП;й; F ) являются зависимыми, так как
При изучении вопросов моделирования гидравлических явлений обычно рассматриваются функциональные зависимости, параметры которых можно выразить через три основные размерности: масса [М], длина [L] и время [Т]. Размерность любого члена уравнения может быть выражена произведением некоторых степеней М, L, Т.
Однако эта система единиц измерения (М, L, Т) не является основной. Она стала общераспространенной лишь потому, что используемые в ней величины привычны для наших ощущений. То, что можно выбрать другую систему основных измерений, можно увидеть на анализе закона Ньютона:
Уравнение, выраженное в системе размерности, запишется
то есть это равенство определяет размерность силы в системе единиц массы, длины и времени. Из уравнения (8.39) можно получить размерность массы в другой системе единиц: сила, длина, время
Размерности параметров, встречаемых при решении гидравличе ских и лесосплавных задач, можно выразить через размерности массы, можно получить из зависимости
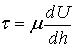
откуда 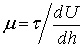
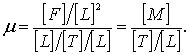
В таблице 8.3 приведены размерности величин, встречающиеся в исследованиях по гидравлике, гидротехнике, гидродинамическом взаимодействии водного потока с лесосплавными объектами. Размерности величин выражены через массу, длину и время (М, L, Т). При рассмотрении некоторых примеров мы будем использовать параметры, выраженные через силу, длину и время (F, L, Т).
В гидравлических исследованиях часто встречаются задачи, которые невозможно решить теоретически, используя математический аппарат. В этом случае прибегают к эксперименту. Исследователь вскрывает физическую картину изучаемого процесса и может составить полную функциональную зависимость, для раскрытия которой могут быть использованы методы анализа размерностей, входящих в зависимость параметров.
Единицы измерения и размерность

Admin
Единицы измерения и размерность
Единицы измерения
Я уже не раз говорил, что число, само по себе, — это ничего не значащая бессмыслица. Иногда это становится особенно очевидно. Допустим, мы зашли в ювелирный магазин и увидели там красивый камушек.
— Сколько он стоит? — хотим мы знать.
— Пятьдесят, — отвечают нам.
Удовлетворил ли такой ответ наше любопытство? — Нет, потому что «пятьдесят» бывают разные, например:
50 копеек,
50 рублей,
50 тысяч рублей.
Пояснительные слова (такие как копейки, рубли, тысячи рублей), стоящие при числах и придающие им смысл, называются единицами измерения или же просто единицами. Число вместе с сопутствующей ему единицей измерения называется величиной. При решении практических задач, опускать единицы измерения допустимо только в том случае, если мы заранее договоримся, какие именно единицы мы используем. Например, мы могли бы спросить:
— Сколько рублей стоит этот камушек?
Тогда ответ: «Пятьдесят», — оказался бы вполне осмысленным и исчерпывающим.
Рассмотрим такую задачу. У Дениса в одном кармане — 1,5 тысяч рублей, а в другом — еще 300 рублей. Спрашивается, сколько всего у Дениса денег? Очевидно, содержимое обоих карманов надо сложить, и чисто формально решение задачи можно записать так:
1,5 тыс. руб. + 300 руб.
С практической точки зрения, однако, подобное решение является неудовлетворительным. Допустим, мы хотим проделать вычисления с помощью калькулятора. В калькулятор нельзя ввести никаких единиц измерения, а только «голые» числа. Как тут быть? Очевидно, единицы измерения придется просто отбросить. Но не так:
1,5 + 300,
потому что в этом случае получается полная чушь. Нам нужно, прежде всего, договориться об общей единице измерения для обоих слагаемых. Пусть это будет, например, рубль. Мы знаем, что
тыс. руб. = 1000 руб.
Поэтому, сделав подстановку, мы можем переписать нашу сумму в таком виде:
1,5 тыс. руб. + 300 руб. =
1,5 ∙ 1000 руб. + 300 руб. =
1500 руб. + 300 руб.
Таким образом, мы выразили все слагаемые в одинаковых единицах измерения, а именно — в рублях. Теперь эти единицы измерения позволительно отбросить, чтобы проделать вычисления на калькуляторе:
1500 + 300 = 1800.
Получив численный ответ, мы восстанавливаем отброшенную ранее единицу измерения и получаем окончательно
1800 руб.
Подобным же образом задачу можно решить, проделав вычисления в тысячах рублей:
1,5 тыс. руб. + 300 руб. = (делаем подстановку) =
1,5 тыс. руб. + 300 ∙ 0,001 тыс. руб. = (упрощаем) =
1,5 тыс. руб. + 0,3 тыс. руб. = (отбрасываем ед. измерения) =
1,5 + 0,3 = (считаем на калькуляторе) =
1,8 = (восстанавливаем ед. измерения) =
1,8 тыс. руб.
Или же в копейках:
1,5 тыс. руб. + 300 руб. =
1,5 ∙ 100000 коп. + 300 ∙ 100 коп. =
150000 коп. + 30000 коп. =
150000 + 30000 =
180000 =
180000 коп.
Ответ мы во всех случаях получили одинаковый, потому что
1800 руб. = 1,8 тыс. руб. = 180000 коп.
На этих примерах мы видим, что
О размерностях физических величин
О термине «физическая размерность»
Термин “размерность” имеет совершенно разные значения в математике (геометрии) и физике. В математике размерность некоторой количественной меры (величины, параметра, переменной, константы и пр.) есть также количественная мера, определяющая степень, в которую возводится некая первичная по отношению к определяемой величины мера, в отношении которой (первичной меры) определяется размерность. То есть
В физике формальное определение размерности дано в советском ГОСТ 16263-70 (ГСИ. Метрология. Термины и определения), который действует в России и Казахстане и в настоящее время:
В БСЭ имеется другое, неверное определение размерности:
[авт.: Коган Б. Ю., то же: Коган Б. Ю., Размерность физической величины, М., Изд-во «Наука», 1967, 72с. с илл., 100000 экз.]
Это определение не соответствует ни стандарту, ни смыслу понятия физической размерности. Кроме того, размерность физической величины и единица измерений физической величины синонимами не являются.
В Международной системе величин (англ. International System of Quantities, ISQ), на которой базируется Международная система единиц (СИ), в качестве основных величин выбраны длина, масса, время, электрический ток, термодинамическая температура, сила света и количество вещества. Символы их размерностей в СИ приведены в таблице[1].
Таблица 1. Основные физические размерности в СИ
Символ для размерности
Количество вещества
Для обозначения производных физических размерностей используют символ dim, а также сочетание размерностей в конкретной системе единиц, например, СИ, заключенные в квадратные скобки.
Например, для скорости при равномерном движении выполняется
Аналогично для размерности ускорения получается
Из уравнения второго закона динамики с учётом размерности ускорения для размерности силы следует:
В общем случае размерность физической величины представляет собой произведение размерностей основных величин, возведённых в различные (положительные или отрицательные, целые или дробные) степени n i
dim X = L n1 M n2 T n3 I n4 Θ n5 M n6 J n7
Показатели степеней n i в этом выражении называют показателями размерности физической величины. Если в физической размерности величины хотя бы один из показателей размерности не равен нулю, то такую величину называют имеющей физическую размерность (качество), а значит, эта величина является реально физической. Если все показатели размерности равны нулю, то рассматриваемая величина есть всего лишь математический коэффициент, количественное соотношение каких-то двух величин, но не реальная физическая величина.
Коррекция размерностей системы СИ в реальной физике
Хотя система СИ наиболее физична из всех используемых систем физических единиц измерений (СГС, СГСЭ и пр.), но на самом деле она не является ни оптимальной, ни даже корректной в отношении физических размерностей. И вот почему.
Основные физические размерности должны быть неразложимы на составные размерности. В СИ это не так. Размерность силы электрического тока является комбинацией размерности заряда и размерности времени
Размерность температуры представляет собой производную размерность от размерности энергии и размерности энтропии
Точно так же обстоит дело с силой света, размерность которой есть сложносоставная величина.
Для исключения нелогичностей и успешности размерностного анализа в реальной физике необходимо использовать систему основных размерностей, показанную в таблице 2.
Таблица 2. Основные физические размерности в реальной физике
Символ для размерности
Электрический заряд
Здесь в основные размерности входит угол, так как наличие размерности угла коренным образом меняет смысл физической величины, что часто не учитывается в СИ.
К примеру, размерность момента силы в СИ равна размерности энергии [N·m] = [J], что есть нонсенс. В реальности в размерность момента силы входит угол [N·m/rad], что соответствует смыслу этой физической величины, ибо [N·m/rad] означает, что указанное в величине количество энергии приходится на каждый радиан.
Без правильного учета размерности энтропии невозможно проводить анализ реальных термодинамических и информационных явлений в физике.
С помощью произведения основных физических размерностей может быть получена размерность любой физической величины
dim X = T n1 A n2 L n3 M n4 C n5 E n6
Системы единиц измерения физических величин
Наиболее рациональной для применения в физике видится система СИ, которая применяется в качестве стандарта во многих странах и наиболее точно соответствует физической сущности величин. Именно она с некоторыми корректировками используется в реальной физике.
В СИ размерность любой физической величины записывают, как произведение символов, которыми именуются физические размерности, каждый из которых возведён в рациональную степень.
Например, размерность скорости — расстояние, делённое на время [m/s], а размерность силы — масса, умноженная на расстояние и делённая на время в квадрате [kg·m/s 2 ]. Выражение размерности для вычисляемой величины (количества) записывается в квадратных скобках.
В механике размерность любой величины может быть выражена через расстояние [m], массу [kg] и время [s]. Электрические и магнитные величины также могут быть выражены через эти три размерности плюс размерность электрического заряда в Кулонах [C]. Для рассмотрения существа физического процесса (его реального качества) часто удобнее использовать составные, то есть производные от базовых, размерности, такие, как размерность электрического тока [a] = [C/s], силы [N] = [kg·m/s 2 ], энергии [J] = [kg·m 2 /s 2 ] и пр.
Любая физическая величина имеет физическую размерность как атрибут ее качества, если у какой-либо величины нет физической размерности (говорят, что она «безразмерна»), то это не физическая величина, а только некий относительный математический коэффициент, отношение между двумя другими физическими величинами одной и той же размерности.
К сожалению, последнего не понимают многие математики («физико-математики»). Они пытаются присвоить смысл самостоятельной физической величины таким коэффициентам или даже построить целые безразмерные «физико-математические» системы единиц, не понимая, что без качества физической размерности такие системы сами не имеют физического качества, но являются лишь количественно-математическими моделями, толерантными к логическим ошибкам. То есть такие математические модели допускают нарушение логики в результате подмены одного физического качества другим, просто не видя физического качества.
К таким системам относятся релятивистский вариант системы СГСЭ, релятивистская система безразмерных единиц (которую не следует путать с системой естественных единиц Макса Планка), система MLT, и прочие разновидности систем, пытающихся выбросить из физики ее физическое качество, то есть содержание, и сделать физику разделом математики. К примеру, в системе MLT (масса-длина-время) исключены другие физические качетва, отнюдь не сводимые к массе, длине и времени. Среди них углы (плоские и телесные) и электрический заряд.
Основные физические размерности и единицы измерений в СИ приведены в таблице.
Физические размерности в Международной системе единиц (СИ)
t
α
θ
ε
l
S
V
v
a
r
ν
φ
d
μ
m
p
F
момент количества движения
K
T
M
P
η
Za
za
Zm
J
W
P
T
q
Me
D
P
U
E
ε
C
εa
κa
I
X
ρ
σ
P
Q
Ф
L
R m
Печально, что составители российских метрологических нормативных документов запретили использование термина «системы единиц измерения физических величин», разрешая использование лишь термина «системы единиц физических величин», не понимая, что любая единица физической величины имеет смысл только в процессе физических измерений и для него. Любая метрологическая информация поступает к нам (в измерительный прибор) только в процессе измерения, а само измерение возможно лишь при использовании единиц измерения.
Проверка физической размерности
В формулах, имеющих физический смысл, только величины, имеющие одинаковую размерность, могут складываться, вычитаться или сравниваться. Например, сложение массы какого-либо предмета с длиной другого предмета не имеет смысла. Также невозможно сказать, что больше: 1 килограмм или 3 секунды. Из этого правила, в частности, следует, что левые и правые части всех физических уравнений должны иметь одинаковую размерность.
Эти правила используются для проверки правильности физических формул. Если в полученном уравнении какое-то из них нарушается, то ясно, что, в качественной модели анализируемого физического процесса была допущена ошибка, которая делает бессмысленными результаты всех количественных (математических) операций.
Анализ физических размерностей
Для исключения нарушения логики качественно-логический анализ всегда должен предшествовать количественному, ибо он является анализом более высокого иерархического уровня, нежели количественно-математический.
Для проведения качественно-логического анализа составляют уравнения размерностей, которые составляют путем замены физических величин (параметров) обозначением их физических размерностей. При этом левая и правая часть уравнения после приведения к подобным размерностям должны иметь эквивалентные размерности.
Пример анализа физической размерности
Физическое уравнение: F = m·a
Уравнение размерностей до приведения: [N] = [kg·m/s 2 ]
Уравнение размерностей после приведения: [kg·m/s 2 ] = [kg·m/s 2 ]
При этом множество формул, описывающих данную систему или процесс, сужается до узкого перечислимого множества вариантов (с точностью до безразмерной константы). Суть метода заключается в том, что из параметров, характеризующих систему, составляется выражение, имеющее нужную размерность. При этом нельзя забывать, что это лишь метод подгонки, единственность решения которого еще предстоит доказать.
Как уже было отмечено, при анализе размерностей формул размерность левой части уравнения должна быть равна размерности правой части уравнения. Отсутствие такого равенства говорит о неверности формулы. Однако наличие такого равенства не является достаточным условием справедливости выводимой формулы.
Степени физических размерностей
В выражениях размерности часто встречается некоторая степень, то есть физическая размерность [x] может быть какой-то степени n : x n :
При этом n может быть не только целым числом, но и дробным:
Появление дробной степени в физической размерности соответственно означает, что физическая величина, имеющая такую дробную размерность проявляет свойство аддитивности (меры) по отношению базовой физической размерности именно в этой дробной степени. Примером могут служить различные спектральные меры, являющиеся функцией частоты или энергии в дробной степени, например [Hz 1/2 ] или [J 1/2 ], когда аддитивной мерой от частоты в первой степени является энергия сигнала, а используется выражение для амплитуды или нормы сигнала (см. «Энергетические спектры сигналов»). То же самое относится к физическим мерам, аддитивным к объемам. В них может быть размерность [m 1/3 ].
«Безразмерные» физические величины
В отличие от спекулятивно-математической физики, пытающейся отказаться от физических размерностей для формального замыкания теоретической физики на математическую релятивистскую модель, в реальной физике кроме физических величин, характеризуемых физическим качеством, существуют и величины, характеризующие чисто количественные отношения между физическими величинами. Именно их можно считать «безразмерными», но реально имеющими, как минимум, количественно-математическое качество, обычно [раз, доля, %, дБ], проявляющееся при делении величин физического качества одной и той же физической размерности. В таблице ниже приведены некоторые «безразмерные» величины, используемые в физике. Как правило, они называются коэффициентами.
