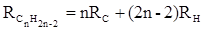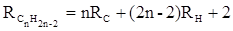Рефрактометрия это в химии что такое
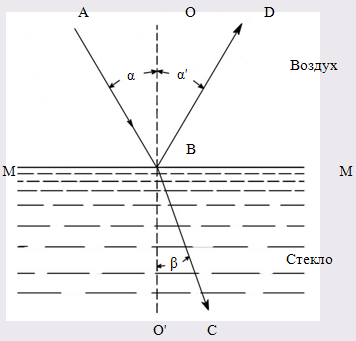
Рефрактометрический анализ основан на измерении показателя преломления жидкого анализируемого вещества (или его раствора). Луч света, проходя из одной прозрачной среды (воздух) в другую (жидкость), падая наклонно к поверхности раздела фаз, меняет свое первоначальное направление, т.е. преломляется (рис. 117). Отношение синуса угла падения a к синусу угла преломления b является постоянной величиной для данных двух сред и называется показателем преломления среды II по отношению к среде I (средой I обычно является воздух):
Показатель преломления n является характерной величиной для каждого индивидуального вещества, он зависит от длины волны падающего света, температуры, давления и концентрации (если это раствор).
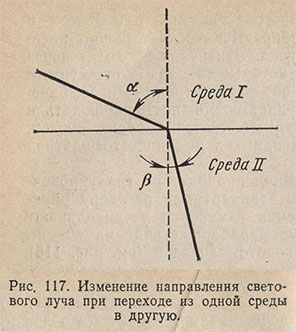
При некотором угле падения угол преломления может оказаться равным 90° (sinb = 1); в этом случае преломленный луч света будет скользить по поверхности раздела сред. Угол падения луча, при котором наблюдается это явление, называется лучом полного внутреннего отражения.
Основной частью любого рефрактометра являются две призмы, между которыми помещают слой анализируемой жидкости. Пучок света проходит через первую призму, затем, преломившись в слое исследуемой жидкости, претерпевает полное внутреннее отражение от поверхности второй призмы. Линия, ограничивающая область полного внутреннего отражения, представляет собой границу света и тени и наблюдается через окуляр прибора.
Рефрактометрический метод широко применяется для идентификации и определения чистоты многих органических веществ, а также для количественного анализа растворов. Для проведения количественных определений по показателю преломления предварительно строят градуировочный график.
Рефрактометр РЛ и работа с ним
Рефрактометр лабораторный является наиболее простым по устройству и обращению (рис. 118). К штативу рефрактометра на изогнутой ручке прикреплено вогнутое зеркало 8, с помощью которого луч света направляют на окошко призмы. Для проверки нулевой точки прибора (по дистиллированной воде) наносят пипеткой 1-2 капли воды на полированную поверхность измерительной (нижней) призмы, опускают и закрепляют винтом верхнюю призму, затем устанавливают окуляр прибора на резкость (вдвигая или выдвигая его) по глазам наблюдателя. Если нулевая точка смещена (показатель преломления воды равен 1,3330 при 20°С), то через люк 7 ключом подвинчивают регулировочный винт так, чтобы шкала показывала точно значение 1,3330.
Нижнюю призму тщательно протирают фильтровальной бумагой и на нее наносят 1-2 капли исследуемой жидкости, опускают верхнюю призму и производят отсчет показателя преломления. Через окуляр 4 виден участок шкалы 6. На шкале 6 нанесены значения показателя преломления в интервале от 1,300 до 1,540. Окуляр направляют так, чтобы видимая граница раздела между светлой и темной частями поля зрения совпала с тремя метками, нанесенными по диаметру окуляра. Если пограничная линия размыта и окрашена в разные радужные цвета, отсчет по шкале прибора производить нельзя. С помощью ручки винта-компенсатора 3 добиваются четкой границы раздела между светлой и темной частью поля зрения.
По окончании измерений призмы следует промыть дистиллированной водой, этанолом, тщательно протереть фильтровальной бумагой или фланелью, не допуская царапин на поверхностях призм. Нельзя трогать призмы руками во избежание загрязнения.
Рефрактометр Аббе
Имеет шкалу для отсчета показателя преломления от 1,300 до 1,700. Измерения могут проводиться в проходящем и в отраженном свете. Главными узлами рефрактометра (рис. 119) являются призменный блок 3, установочная лупа 1 и стеклянный лимб с отсчетным микроскопом 5.
Призменный блок состоит из двух призм (измерительной и осветительной), на поверхности которых тонким слоем распределяется анализируемая жидкость (около 0,05 мл). Призменный блок может быть нормальным или оснащенным проточным приспособлением. Проточный призменный блок предназначается для анализа непрерывно протекающих жидкостей, в том числе и легколетучих. В проточном блоке над поверхностью измерительной призмы имеется узкий промежуток, через который и протекает анализируемая жидкость. Призменный блок термостатируется. Блок имеет собственный источник света (на 6 В и 1,8 Вт), закрепленный зажимным патроном перед измерительной призмой для измерений в проходящем или отраженном свете. Нормальный призменный блок 3 применяется для анализа отдельных проб жидкостей, а также твердых и пластических веществ.
При измерении в проходящем свете световой поток падает в осветительную призму через зеркало 6 или непосредственно от источника света, установленного на призменном блоке, проходит через пробу анализируемого вещества и попадает в измерительную призму. Затем свет поступает в установочную лупу. При измерении в отраженном свете он падает непосредственно в измерительную призму, затем отражается от смоченной пробой поверхности измерительной призмы и попадает в установочную лупу.
При измерениях в обоих случаях в поле зрения окуляра установочной лупы наблюдается светлое и темное поля (рис. 120). Линия раздела между обоими полями соответствует углу полного внутреннего отражения. При измерении в проходящем свете достигается большая контрастность светлого и темного полей; при измерении в отраженном свете оба поля менее контрастны. При освещении белым светом линия раздела сначала получается с цветной каемкой. Эта каемка устраняется вращением маховичка 2 (см. рис. 119) дисперсионного компенсатора. Вращением маховичка 4 устанавливают полученную бесцветную линию на точку пересечения крестовины. При этом одновременно поворачивается лимб. Через микроскоп делают отсчет показателя преломления или содержания сухого вещества в исследуемом растворе, например на рис. 121:
Мутные жидкости, пластические вещества, а также сильно окрашенные жидкости можно измерять только в отраженном свете.
С помощью рефрактометра Аббе определяют концентрацию растворов и проводят испытание жидкостей на чистоту, контроль шлифов, пластичных и твердых веществ. Им можно исследовать водные, спиртовые, эфирные и другие растворы; масла и воски; фруктовые соки, сиропы, сахарные растворы; жиры, растительные масла, настойки, напитки, смолы и пластмассы. Выпускается в СССР и в ГДР.
Рефрактометр Пульфриха PR-2
Интервал измеряемых значений показателя преломления от 1,29 до 1,86. Прибор имеет комплексное оборудование, позволяющее проводить измерение показателя преломления в зависимости от длины волны в видимой области спектра.
На основании прибора 14 (рис. 122) находится осветитель 1 с блоком питания, призменный цоколь для установки измерительной призмы 6 и измерительное устройство 9.
В осветителе размещены три спектральные лампы с соответствующими блоками питания: ртутная лампа высокого давления HgE/2, гелиевая спектральная трубка и водородная трубка (гейслеровская трубка). Лампы по выбору можно включать переключателем 22. Вращающимся диском 23, находящимся на той же оси, приводят в действие приспособление для смены светофильтров. На выходном объективе 19 осветителя имеется цветной светофильтр (синее стекло).
Для смены ламп снимают кожух 4. Юстировку ламп производят с помощью юстировочных винтов 2 и 3. На основании прибора находится главный выключатель питания 21, включатель ртутной лампы 20 и кнопка 18 для кратковременного включения гейслеровских трубок, обеспечивающих максимальную интенсивность излучения. При включенных главном выключателе 21 и выключателе 20 ртутная лампа HgE/2 работает в постоянном режиме. Гейслеровские трубки, наоборот, горят только тогда, когда переключатель 22 установлен на соответствующую трубку. Этот простой метод предупреждает скорый износ гейслеровских трубок.
В призменном цоколе установлена измерительная призма б, под которую помещают исследуемую жидкость или тонкую пластинку исследуемого стекла, предназначенная для измерения рефракции. Призма термостатируется. Для этого к обеим выходным трубкам подключается термостат, обеспечивающий циркуляцию термостатирующей воды через призменную оправу. По термометру со шкалой от 0 до 50 °С с интервалом в 0,1 °С можно считывать температуру с точностью до 0,05 °С.
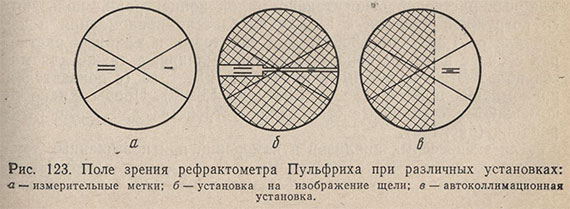
Измерительное устройство содержит зрительную трубу 8, лимб с соответствующими измерительными шкалами и автоколлимационное устройство. Зрительная труба изображает предельную линию, т.е. щель в фокальной плоскости объектива зрительной трубы. В поле зрения рефрактометра находятся измерительные метки в виде штрихов и перекрестьев (рис. 123). Измерительные метки используются для установки измерительного критерия (предельной линии или изображения щели). Перекрестье предпочтительно для измерения предельной линии.
Объектив и измерительная метка зрительной трубы, связанные друг с другом, вращаются. Зрительную трубу поворачивают с помощью Маховичка 13 (см. рис. 122); встроенный механизм точной наводки позволяет чувствительно устанавливать предельную линию или изображение щели.
Измерительные шкалы в приборе освещаются лампой накаливания на 6 В, 5 Вт. В зрительную трубу 8 наблюдают лимб, жестко с ней связанный. Шкала лимба имеет деления в целых градусах в интервале от 15 до 100 °С. С помощью рукоятки 11 совмещают шкалу в целых градусах с нулевым делением вспомогательной минутной шкалы и доли минут отсчитывают по этой шкале. Минутная шкала имеет деления по 0,05′, на глаз отсчет производят до 0,01′.
В приборе имеется автоколлимационное устройство (выключатель 10); оно позволяет удобно юстировать измерительную призму и проверять ее положение во время серийных измерений.
Рефрактометр Пульфриха применяют для измерения показателя преломления оптических и цветных стекол, пластмассовых пластинок, порошков, различных органических жидкостей и водных растворов. Прибор является наиболее точным и надежным.
Погружной рефрактометр
Погружной рефрактометр (рис. 124) применяется для измерения показателя преломления в интервале от 1,32539 до 1,64700 с использованием десяти погружных измерительных призм. Измерительную призму погружают непосредственно в исследуемую жидкость.
Источником света является обычная лампа накаливания в 40 Вт. При работе с погружными призмами обычно достаточно дневного освещения. Выходящий из жидкости скользящий свет проходит через погружную призму 1, затем проходит по очереди через компенсатор 2, объектив 3, носитель шкалы 5 и окуляр 7. Поле зрения разделено на два поля различной освещенности. При использовании немонохроматического света линия раздела поля может иметь цветную каемку, которая устраняется вращением накатного кольца компенсатора 4. Если вещество вызывает большое рассеяние света, то с помощью компенсатора не удается получить совершенно бесцветную линию раздела; в этом случае необходимо пользоваться натриевым источником света. Положение линии раздела определяют по шкале.
Микрометрическим винтом 6 совмещают меньшее деление оптической шкалы с линией раздела и отсчитывают десятые доли деления по шкале барабана микрометрического винта 6.
Для экспрессных анализов и измерений при повышенных температурах применяют термопризмы. Они представляют собой двойные призмы, состоящие из измерительной и осветительной призм; интервал измерения их соответствует интервалу измерения погружных призм. При работе с термопризмами достаточно нескольких капель исследуемой жидкости, которые наносят на рабочие поверхности двойной призмы. Термопризмы позволяют проводить измерение при температуре до 50°С.
К рефрактометру прилагается приспособление с проточной погружной призмой для исследования непрерывно протекающих жидкостей. Она легко устанавливается и легко снимается с рефрактометра. Выпускается в ГДР.
Курсовая работа: Рефрактометрический метод анализа в химии
| Название: Рефрактометрический метод анализа в химии Раздел: Рефераты по химии Тип: курсовая работа Добавлен 22:54:32 08 июня 2011 Похожие работы Просмотров: 14911 Комментариев: 17 Оценило: 5 человек Средний балл: 4.8 Оценка: неизвестно Скачать | ||||||||||||||||||||||||||||||||||||||||||
| Линия спектра водорода | Индекс линии | λ, нм | Обозначение показателя преломления |
| жёлтая | D | 589,3 | nD |
| красная | C | 656,3 | nC |
| синяя | F | 486,1 | nF |
| фиолетовая | G | 434,0 | nG |
На практике используются три способа выражения дисперсии света.
1. Средняя дисперсия:
2. Коэффициент дисперсии или число Аббе:
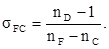
3. Удельная дисперсия:
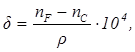
где ρ – плотность вещества.
Поскольку показатель преломления изменяется с изменением температуры и длины волны света (который, безусловно, не должен поглощаться веществом), то первое условие должно быть, строго говоря, оговорено, но на самом деле изменение величины R в зависимости от температуры вполне укладывается в рамки ошибок эксперимента, и поэтому температуру указывать не обязательно.
Если нужно определить молекулярную рефракцию твёрдого вещества, то прибегают к модифицированному уравнению, учитывающему изменение показателя преломления с концентрацией раствора.
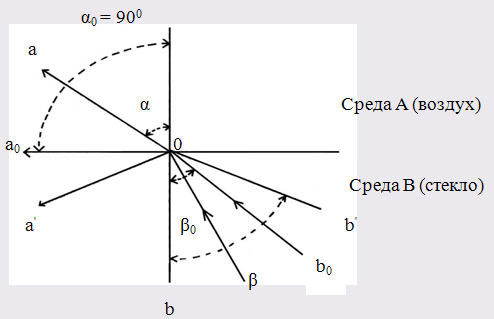
1.4 Полное внутреннее отражение
Рис.2. Схема направления распространения лучей при полном внутреннем отражении
b0 Oa0 – распространение луча при предельном угле;
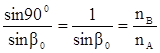
На измерении предельного угла основан принцип работы рефрактометров.
2. Дипольные моменты и рефракция
Коэффициент преломления, как уже отмечалось, зависит от поляризуемости атомов, молекул и ионов. Поэтому исследование электрических характеристик вещества даёт важную информацию о распределении зарядов в молекуле и позволяет установить некоторые свойства вещества, обусловленные его электрической асимметрией.
Рассмотрим некоторые вопросы, касающиеся природы возникновения дипольного момента в молекуле.
2.1 Поляризуемость и дипольный момент
Если распределение ядер и электронов в пространстве таково, что центры «тяжести» положительных и отрицательных зарядов не совпадают, то молекула обладает постоянным дипольным моментом:
где l – расстояние между центрами электрических зарядов.
Такая молекула является полярной. Мерой полярности молекулы служит величина дипольного момента, которую выражают в дебаях (D):
D = 3,33564·10 −30 Кл·м
Дипольный момент – величина векторная. Направление вектора «→»выбирается от отрицательного полюса к положительному. В химической литературе, однако, традиционно принимается противоположное направление, т. е. от «+» к «−».
Если в двухатомных молекулах простых веществ, т. е. состоящих из одинаковых атомов, и в многоатомных молекулах сложных веществ, обладающих высокой симметрией, центры «тяжести» разноимённых электрических зарядов совпадают (l = 0), то такие молекулы не обладают постоянным моментом (μ = 0) и являются неполярными.
Если любую неполярную молекулу поместить в постоянное электрическое поле, создаваемое, например, конденсатором, то происходит её поляризация, выражающаяся в разнонаправленном смещении зарядов (деформационная поляризация). Тяжёлые ядра атомов будут несколько смещаться в сторону отрицательного полюса, а электроны незначительной массой будут легко смещаться в сторону положительного полюса. В результате центры «тяжести» положительных и отрицательных зарядов совпадать не будут, и в молекуле будет возникать индуцированный (наведённый) диполь, момент которого пропорционален напряжённости электрического поля:
где Е – напряжённость внутреннего электрического поля в молекуле [эл. ст. ед./см 2 ; Кл/см 2 ]
Таким образом, в электрическом поле образуется диполь с наведённым или как его называют индуцированным дипольным моментом.
Если любую полярную молекулу поместить в электрическое поле, то будут происходить два процесса. Во-первых, молекула будет ориентироваться вдоль поля, и, во-вторых, расстояние между центрами «тяжести зарядов будет увеличиваться, увеличивая дипольный момент молекулы».
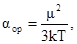
где k – постоянная Больцмана (1,380662(44)∙10 −23 Дж/К);
Т – абсолютная температура, К.
Таким образом, полная поляризуемость молекулы α складывается из трёх величин:
Из уравнений (11) и (12) следует, что полная поляризуемость α будет иметь размерность объёма [см 3 или Å 3 ].
2.1.1 Молярная поляризуемость
В электрическом (электромагнитном) поле молекулы поляризуются и возникает состояние напряжённости, характеризуемое величиной диэлектрической проницаемости (ε) вещества, которая входит в уравнение закона Кулона и может быть определена экспериментально.
Измеряя диэлектрическую проницаемость, характеризующую вещество в целом, можно определить по теории поляризации диэлектриков электрооптические параметры его молекул, связанные с ε формулой Клаузиуса-Моссотти:
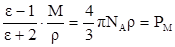
где NA – число Авогадро;
М – молекулярная масса вещества;
Ρ – плотность вещества, г/мл.
РМ – молярная поляризация – величина, характеризующая меру индуцированного момента в объёме, который занимает 1 моль вещества.
Молярная поляризация, дипольный момент и общая поляризуемость молекулы связаны друг с другом уравнением Дебая, которое выводится из уравнений (12) – (14):
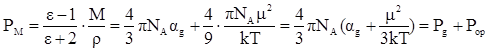
По уравнению Дебая можно вычислить значения α и μ по известным величинам ε, М и ρ.
Поляризация молекул веществ, имеющих сравнительно большие значения ε и Р (например Н2 О, HCN, HCl), зависит от температуры, уменьшаясь при её повышении. Молекулы таких веществ, не имея центра симметрии зарядов, являются постоянными диполями. Для них молярная поляризация в уравнении Дебая выражается линейной функцией от 1/Т:
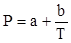
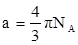
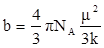
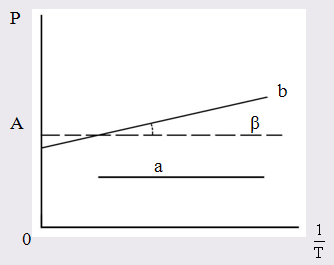
Для случая молекул постоянных диполей (прямая а; рис. 3) отрезок ординаты ОА = а определяет величину поляризуемости α, а tgβ = b – величину дипольного момента μ
Рис. 3. Зависимость молярной поляризации
от обратной температуры
а – для молекулы, постоянных диполей;
b – для неполярных молекул.
2.2 Молярная рефракция
Из электромагнитной теории света Максвелла следует, что для длин волн, значительно удалённых от области их поглощения молекулами вещества, справедливо равенство:
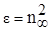
С учётом этого уравнение Клаузиуса-Мосотти (15) принимает следующий вид:
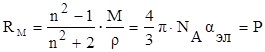
На практике часто пользуются показателем удельной рефракции r, то есть рефракцией одного грамма вещества. Удельная и молярная рефракции связаны соотношением: R = r∙M, где М молярная масса.
Поскольку в уравнении (19) N пропорционально плотности, то его можно представить в следующем виде:
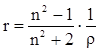
Х. Лорентц и Л. Лоренц вскрыли физический смысл понятия рефракции – как меры электронной поляризуемости и подвели под учение о рефракции прочный теоретический фундамент.
Величина удельной рефракции практически не зависит от температуры, давления и агрегатного состояния вещества.
В исследовательской практике кроме молярной и удельной рефракции RМ и r используют и другие производные от показателей преломления n(табл. 2).
Показатель преломления неполярных веществ практически не зависит от частоты волн света и поэтому уравнение (19) справедливо при всех частотах. Например, для бензола n 2 = 2,29 (длина волны 289,3 нм), тогда как ε = 2,27. поэтому, если для приближённых расчётов рефракции достаточно пользоваться показателем преломления видимого спектра, то для точных расчётов необходимо производить экстраполяцию по формуле Коши:
где nλ – показатель преломления при длине волны λ;
а – эмпирический коэффициент.
Таблица 2 Рефрактометрические константы
| N | Наименование | Обозначение | Область применения |
| 1 | Показатель преломления | n | Характеристика чистоты веществ. Анализ двойных систем веществ |
| 2 | Удельная рефракция | r | Характеристика чистоты веществ. Определение концентрации веществ |
| 3 | Молекулярная рефракция | R | Определение значений некоторых атомных и молекулярных констант. Определение строения органических молекул |
| 4 | Относительная дисперсия | σ | Анализ сложных смесей. Определение строения органических молекул |
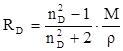
Обычно индекс D опускают и формулу записывают как уравнение (19).
3. Рефракция и структура молекул
3.1 Аддитивность рефракции
Рефракция, является аддитивной величиной. Использование рефрактометрии в науке было начато в середине XIX века, когда обнаружили, что между молекулярными рефракциями соседних членов гомологического ряда органических соединений выполняется простое соотношение:
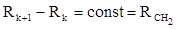
Согласно этому соотношению молекулярную рефракцию k-го члена гомологического ряда можно представить в виде суммы молекулярных рефракций первого члена ряда и k−1 группы СН2 :
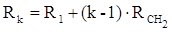
Впоследствии было обнаружено, что ряд изомеров также имеют одинаковые молекулярные рефракции. Это обстоятельство позволило предположить, что молекулярная рефракция вещества зависит только от природы и числа атомов в молекуле и может быть вычислена простым суммированием характерных для каждого элемента атомных рефракций:
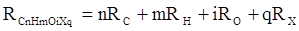
где 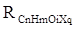
Было установлено и то, что молекулярная рефракция большого числа органических соединений может весьма отличаться от суммы составных рефракций. К простейшим соединениям такого типа относятся этиленовые углеводороды и их алкилпроизводные. Этот класс соединений всё же был включён в аддитивную схему путём учёта того обстоятельства, что в этих соединениях имеются двойные связи типа С=С, аналогично был произведён учёт наличия тройных связей С≡С, которыми характеризуются ацетиленовые соединения.
Таким образом, рассчитывая рефракцию молекулы через рефракции составляющих её атомов и фрагментов, следует учитывать валентные состояния атомов – инкременты (вклады) рефракций двойных и тройных связей, а также поправки на особое положение отдельных атомов и атомных групп в молекулах:
где RА и R1 – соответственно атомные рефракции и инкременты связей (табл. 3, 4).
Поляризуемость ионов. В органической химии большое значение имеет поляризуемость анионов. Существует несколько наборов рефракций ионов. Определяемых либо в растворах, либо в твёрдом или газообразном состоянии.
1. Рефракции и, следовательно, поляризуемости увеличиваются с увеличением размера иона в пределах одной группы периодической системы химических элементов.
3. Анионы с большим зарядом легче поляризуются, чем с меньшим.
Наличие координационной (донорно-акцепторной, семиполярной) связи в молекуле вызывает уменьшение рефракции по сравнению с суммой рефракций индивидуальных молекул, образующих эту связь.
Например: величины R для (СН3 )3 N + –B¯F3 и (C2 H5 )2 O + −B¯F3 примерно на 3,5 и 2,0 см 3 меньше суммы величин R для этих компонент [(CH3 )3 N – триметиламина, (С2 Н5 )2 О – диэтилового эфира и BF3 – трёхфтористого бора].
Согласно второй схеме, величина R для этилового спирта определяется как сумма рефракций групп (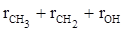
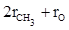
Эти схемы не дают идентичных значений для одного и того же соединения, а также ни одна из них не даёт строго аддитивных значений.
Одна из главных трудностей, с которыми приходится сталкиваться, – это решение вопроса о вкладе в общую поляризуемость, вносимом несвязанными парами электронов гетероатомов таких групп, как С–Х, С–О, С–N.
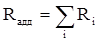
Так, например, молекулярная рефракция нафтеновых углеводородов (алициклов) Сn H2 n может быть вычислена как сумма атомных рефракций углерода RC и водорода RH :
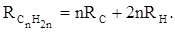
Поскольку основной вклад в общую поляризуемость молекул дают легко поляризуемые внешние (валентные) электроны, 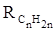
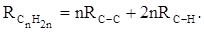
Однако молекулярная рефракция изомерных нафтенов олефинов, содержащая очень легко поляризуемые π-связи, заметно больше. В системе атомных рефракций повышенный вклад С=С-связи учитывается добавлением постоянного слагаемого – инкремента двойной связи.
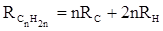
В системе связевых рефракций сумма содержит иные слагаемые:
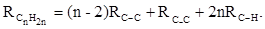
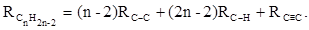
Весьма важно, что изомерные ацетиленовые соединения с двумя двойными связями имеют иные (ещё больше) значения молекулярной рефракции, а именно – в системе атомных рефракций и инкрементов:
или в системе связевых рефракций:
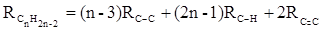
При этом только диены с изолированными и кумулированными (алленовыми 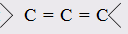
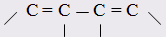
Главной причиной экзальтации является π–π-сопряжение простых связей, и величина экзальтации быстро возрастает с увеличением длины сопряженных систем. Однако частичное или полное включение сопряжённой системы в цикл, а также образование простейших ароматических структур приводит к снижению экзальтации, так что углеводороды ряда бензола и большинство их производных не обнаруживают экзальтации при расчёте аддитивных значений по формуле кекуле. Правилу аддитивости подчиняются не только ароматические соединения с несколькими изолированными бензольными кольцами, но соединения с конденсированными кольцами (нафталины, антрацены, фенантрены) и сопряженными (непосредственно соединенными) кольцами. Эти соединения так же проявляют эффект экзальтации.
Для структурного анализа имеет значение также тот факт, что величина экзальтации существенно зависит от разветвлённости углеродного скелета в месте расположения сопряжённой системы: появление боковых цепей у центральных С-атомов сопряжённых связей влечёт за собой снижение экзальтации, так что в группах изомеров. В пределах одного гомологического ряда с данной сопряжённой системой экзальтация зачастую возрастает пропорционально массе.
Для характеристики сопряжённых систем предлагалось использовать экзальтации, приведённые к молекулярной массе 100 а.е.м. – так называемые удельные экзальтации (Е∑):
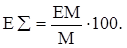
р-π-сопряжение неподелённых электронных пар (галогенов, азота, кислорода) с π-электронами соседних кратных связей проявляется в разных структурах весьма различно.
У непредельных галогенпроизводных эти эффекты столь невелики, что при расчётах по классической аддитивной схеме вообще не учитываются, а у галогенангидридов карбоновых кислот, RCOGal, амидов RCONH2 и ароматических аминов ArNH2 они по сложившейся традиции учитываются введением особых (повышенных) значений атомных или связевых рефракций галогенов и азота в таких структурах и, следовательно, формально не рассматриваются как экзальтации. Понятие «экзальтация рефракции» является, таким образом, весьма условным, связанным с примитивностью самой классической аддитивной схемы и её историей, но всё же полезным для выявления и классификации, содержащихся в исследуемом веществе сопряжённых систем. В современных, более детализированных аддитивных системах, учитывающих состояние гибридизации соседних атомов и влияние непосредственно не связанных атомов, понятие «экзальтация» вообще не используется. Однако такие схемы, разработанные для расчёта свойств органических соединений, требуют установления большого числа исходных аддитивных констант, предъявляют повышенные требования к чистоте исследуемых веществ и в повседневной практике структурного анализа не используются. Возможности структурного анализа по молекулярной рефракции, основанного на классической аддитивной схеме расчёта, ограничиваются информацией о числе и природе кратных связей и об эффектах сопряжения. В рамках выявления этих особенностей структуры обе разновидности классической аддитивной схемы (атомная и связевая) практически равноценны по точности и границам применимости.
Молярную рефракцию атомов, построенных из ионов, рассчитывают как сумму ионных рефракций (табл. 4).
Приступая к установлению строения вещества по молекулярной рефракции, следует, прежде всего, обеспечить необходимую точность исходных данных. Экспериментальные величины показателя преломления и плотности должны иметь погрешность до нескольких единиц четвёртого десятичного знака, легко достижимую на обычных лабораторных рефрактометрах предельного угла и при работе с пикнометрами объёмом более 1 – 2 мл с термостатированием до 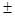
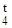
При вычислениях надо употреблять точное значение М согласно установленной или предполагаемой брутто-формуле, а не непосредственно результат приближённого экспериментального определения, так как погрешности большинства обычных физико-химических методов определения молекулярной массы достигают нескольких процентов и сопоставимы с величиной самих структурных влияний на молекулярную рефракцию.
Уравнение (26) выражает правило аддитивности молярной рефракции.
Физически более обоснован способ расчёта рефракции как суммы рефракций не атомов, а связей (табл. 5).
Таблица 4 Ионные рефракции
Правило аддитивности молярной рефракции используют для установления строения молекул, сравнивая R, найденную экспериментально, с рассчитанной по уравнению (26) для предлагаемой структуры молекулы. Близость значений Rэксп. и Rвыч. служит подтверждением строения молекулы (табл. 6). Расхождения до 0,3 – 0,4 мл/моль обусловлены возможными ошибками эксперимента и неточностью собственно аддитивных констант, а для ионных соединений отклонения от аддитивности дополнительно связаны с взаимной поляризацией ионов.
Закономерности рефракций связей.
1. Константы связей какого-либо элемента с атомами других элементов, принадлежащих к одной и той же группе периодической системы, увеличиваются с увеличением размера атома.
Например: C–F C=C > C−C (табл. 3)
Причем двойная связь имеет величину, более чем вдвое превышающую величину для одинарной связи (rC = C > 2rC − C ). Это показывает, что π-электроны гораздо легче поляризуются, чем σ-электроны. Исключением из этого правила является, по-видимому, двойная связь N=O.
4. Для констант связей С=С, C=N и С=О обнаруживается характерная связь с положением элементов в группах и периодах периодической системы, и эти константы уменьшаются по мере роста электроотрицательностей неодинаковых атомов в соответствии с данным порядком перечисления, а константы для связей C=S и С=О уменьшаются в приведённом порядке. Значительное различие между величиной констант для С=О и C=S ( гораздо больше, чем различие между С−О и C−S) связано с тем, что атом серы не склонен к образованию двойной связи с углеродом и поэтому проявляет, находясь в этом состоянии, сильный М-эффект.
Учитывая указанные тенденции, следует иметь в виду, что точные величины рефракции связей довольно сильно меняются при изменении молекулярного окружения связей, и поэтому будет наблюдаться большее или меньшее отклонение наблюдаемых молекулярных рефракций от величин, рассчитанных на основании стандартных или средних значений.
Например, значения молекулярных рефракций для изомеров бутина
Таблица 5 Рефракции связей для D-линии спектра натрия при 20 0 С
Для соединений с одинаковой эмпирической формулой, но с разным химическим строением рефракция различна. Поэтому, экспериментально определяя рефракцию и сравнивая её с вычисленным значением, можно установить химическое строение исследуемого органического соединения.
Примеры структурного анализа по молекулярной рефракции
Необходимой предпосылкой успешного проведения структурного анализа по молекулярной рефракции является полное использование информации, содержащейся в самой брутто-формуле. Её следует сопоставить с формулами предельных соединений с тем же числом углеродных атомов, и по разнице в содержании водорода сделать заключение о степени непредельности анализируемого вещества и возможном содержании в нём кратных связей и циклов.
1. Совпадение R и RАДД с погрешностью в несколько десятых долей миллилитров в моле подтверждает вероятность, как предполагаемой брутто-формулы, так и структуры. При этом расхождения до 0,3 – 0,4 относятся за счёт приближённого характера самих аддитивных констант, возможных ошибок измерений и влияния примесей. Если при расчёте предполагалось наличие двух и более кратных связей, то совпадение с экспериментальной величиной свидетельствует о том, что кратные связи изолированы друг от друга, кумулированы или образуют простейшие ароматические структуры (бензольное кольцо, некоторые гетероциклы). Окончательные формулировки выводов, как правило, должны учитывать вероятность нескольких структур, неразличимых по молекулярной рефракции в указанных пределах погрешности расчётов.
2. Расхождение R и RАДД более чем на 0,3 – 0,4 мл/моль указывает на ошибочность сделанных при подсчёте RАДД предположений о строении и составе органического соединения или свидетельствует об особенностях структуры, вызывающих экзальтации молекулярной рефракции. В этом случае необходимо рассмотреть другие возможные при данной брутто-формуле значения RАДД для иного числа и природы кратных связей или напряжённых колец, а также иных функциональных групп. Превышение экспериментальной величины R над аддитивной, вычисленной для структур с двумя и более кратными связями, может быть экзальтацией молекулярной рефракции, вызванной сопряжением. Сопоставление величины экзальтации с литературными (табличными) данными для хорошо изученных сопряжённых систем может дать дополнительную информацию о характере сопряжённой системы и разветвлённости углеродного скелета в месте её расположения.
Таким образом, в области видимого света поляризуемость молекул практически полностью обусловлена смещением π-электронов, и поэтому для органических соединений она равна сумме эффективных смещений отдельных электронов. Последнее обстоятельство придаёт молекулярной рефракции свойство аддитивности для составляющих фрагментов молекулы, что находит широкое применение при определении состава и строения молекул.
3.3 Дисперсия молекулярной рефракции
Дисперсией рефракции называется зависимость рефракции или показателя преломления света от длины волны. При нормальной дисперсии показатель преломления n возрастает с уменьшением длины волны. Дисперсию можно охарактеризовать, как разность значений рефракции одного и того же соединения при двух различных длинах волн α и β (Rα – Rβ ). Однако обычно в качестве меры дисперсии используют безразмерную величину – относительную дисперсию:
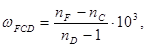
3.4 Рефракция и размеры молекул
Рефракцию можно использовать для вычисления не только электронной поляризуемости молекулы или иона (по уравнению 19), но и для расчёта эффективного радиуса частицы (атома, иона). Поскольку рефракция имеет размерность объёма, отнесённого к определённому количеству вещества (удельная – к одному грамму, молярная – к одному молю), то можно (условно) рассматривать молекулу как сферу с радиусом rм и проводящей поверхностью. В этом случае:
Тогда из уравнения (19) получим:
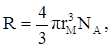
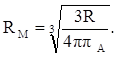
4. Рефрактометрия растворов
Аддитивность рефракции характерна и для жидких смесей (растворов). Рефракция смеси равна сумме рефракций компонентов, отнесённых к их долям в смеси.
Молярную и удельную рефракции двухкомпонентной смеси можно соответственно представить в виде следующих уравнений:
Уравнения (37) и (38) используются для определения состава смеси и рефракции её компонентов.
Рефрактометрия достаточно широко применяется для идентификации веществ, а также для оценки степени их чистоты. При идентификации, а также определении чистоты веществ критерием служит совпадение показателей преломления исследуемого образца и заведомо известного чистого соединения. Важно, чтобы все измерения n выполнялись при одинаковой температуре и при одних и тех же длинах волн.
Если образец загрязнён, то его можно рассматривать как разбавленный раствор примесей в исследуемом соединении. При этом в случае незначительного содержания примесей их концентрацию Сх можно определить, воспользовавшись линейным соотношением:

где n и nчист. – показатели преломления образца и чистого вещества;
К – коэффициент, определяемый экспериментально.
Для ориентировочной оценки величину Сх можно определить, исходя из аддитивности показателей преломления. Чувствительность этого метода тем выше, чем сильнее различаются показатели преломления примесей и чистого органического соединения. Рефрактометрический метод иногда применяется для контроля за процессом очистки вновь синтезированных органических соединений, показатели преломления которых ещё не известны. Если при очистке образца различными способами показатель преломления от одной очистки к другой продолжает изменяться, то органическое соединение не считают чистым (индивидуальным), и процесс очистки продолжают.
4.1 Анализ двухкомпонентных растворов
По значению показателя преломления бинарного раствора можно определить его концентрацию. Для этого необходимо, чтобы была известна зависимость показателя преломления от состава раствора. Для ряда растворов (например, сахарозы, некоторых спиртов, кислот, оснований, солей) зависимости показателей преломления установлены и сведены в таблицы, которыми и пользуются при количественном анализе. Если таких таблиц нет, то используют градуировочные графики, которые строят по результатам измерений эталонных растворов.
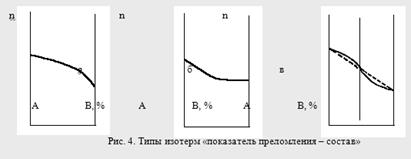
Кривые зависимостей показателя преломления от состава бинарных растворов существенно изменяются с изменением природы раствора. Эти кривые подразделяют на три типа:
I тип – изотермы, имеющие незначительную положительную или отрицательную кривизну, когда изменение n от состава отличается от линейного хода по величине не более, чем на 0,0075-0,008 (рис. 4а);
II тип – изотермы, имеющие заметную кривизну, когда Δn > 0,008 (рис. 4б);
III тип – изотермы с сингулярной точкой (рис. 4в).
Большинству бинарных растворов соответствуют кривые I-го типа. Сюда относятся нормальные растворы и растворы с ассоциированными компонентами, а также растворы с химическим взаимодействием компонентов и растворы, в которых по каким-либо причинам такое взаимодействие не проявляется отчётливо на изотерме «показатель преломления – состав».
К растворам типа II и III относятся растворы с сильно выраженным химическим взаимодействием компонентов и с образованием частично диссоциированных соединений. В некоторых случаях по положению сингулярной точки на кривой III-го типа удаётся определить стехиометрический состав образовавшегося соединения.
Таким образом, в рефрактометрии двухкомпонентных систем, используется помимо количественного физико-химический метод анализа, который позволяет обнаружить достаточно выраженное взаимодействие компонентов. При отсутствии межмолекулярного взаимодействия, приводящего к ассоциации компонентов, справедливо свойство аддитивности рефракции. В этом случае молярная рефракция раствора RР равна сумме произведений рефракций его компонентов и их мольных долей в этом растворе:
где R1 и R2 – молярные рефракции соответственно растворителя и растворённого вещества; N1 и N2 – мольные доли растворителя и растворённого вещества.
Для расчёта RР с использованием экспериментальных данных по уравнению (15) необходимо знать величины «среднемолекулярной массы» раствора, которая определяется соотношением:
Свойством аддитивности, подобно молекулярной рефракции, обладает и удельная рефракция:
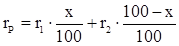
4.2 Анализ трёхкомпонентных растворов
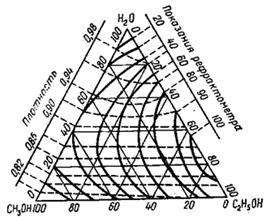
Для анализа тройных систем необходимо знать два каких-либо независимых, характеризующих состав системы, параметра. Одним из таких параметров обычно служит показатель преломления, а вторым – как правило, плотность раствора. Состав смеси по значениям этих параметров можно определить графически. Для этого сначала готовят трёхкомпонентные смеси известного состава и строят зависимость «состав – свойство». Зависимость значений показателя преломления и плотности раствора от состава системы представлена на рис. 5. посредством, так называемой тройной диаграммы (треугольник Гиббса – Розебома). Осями координат служат стороны равностороннего треугольника, на каждой из которых откладывается массовая доля бинарной системы, вершины треугольника соответствует 100 % компонентам, а любая точка внутри треугольника определяет состав трехкомпонентной системы. Определив ρ и n стандартных растворов, наносят на диаграмму изоденсы по точкам, соответствующим составам и имеющим одну и ту же плотность, и изорефракты – по точкам, определяющим состав равнопреломляющих смесей. Из окончаний изоденс и изорефракт опускают перпендикуляры на дополнительные шкалы (линии, проведённые параллельно боковым сторонам треугольника), плотности и показатели преломления соответствующие значениям этих величин.
При проведении анализа измеряют плотность и показатель преломления исследуемого образца и определяют точку, отвечающую составу, на пересечении изорефракты изоденсы. Из этой точки проводят линии, параллельные сторонам треугольника, и по отсечённым этими линиями отрезкам определяют состав анализируемой смеси.
Подробно методика построения тройных диаграмм описана в методических указаниях по физической химии «Изучение взаимной растворимости жидкостей в трёхкомпонентных системах» [14].
5. Рефрактометрия полимеров
Рефрактометрический метод достаточно часто применяют при анализе высокомолекулярных соединений. Этот метод впервые был предложен и впоследствии нашёл широкое применение для количественного определения стирола в продуктах его сополимеризации с дивинилом (1,3-бутадиен). Методика [9] позволяет с погрешностью до 5 % установить число содержащихся в сополимерах звеньев дивинила, присоединённых в положения 1-2, а также температуру стеклования таких полимеров с погрешностью до 3–4 0 С.
Рефрактометрический метод применяется и для исследования кристаллизуемости хлоропреновых каучуков. При помощи этого метода можно определить степень кристалличности образцов полихлоропрена, закристаллизованных при разных температурах [8].
При переходе от одного углеводородного полимера к другому поляризуемость молекулы существенно не меняется, однако замена атомов водорода на атомы галогенов приводит к изменению поляризуемости полимеров и соответственно к изменению их показателя преломления
Рефрактометрия является простым и удобным методом исследования процессов кристаллизации и плавления полимеров, подвергшихся кристаллизации в различных температурных условиях.
Таблица 6 Показатели преломления полимеров
| Полимер | N |
| Политетрафторэтилен (тефлон) | 1,35 – 1,38 |
| Полихлорфторэтилен | 1,39 – 1,43 |
| Ацетат целлюлозы | 1,46 – 1,50 |
| Поливинилацетат целлюлозы | 1,47 – 1,49 |
| Полиметилметакрилат | 1,48 – 1,49 |
| Полипропилен | 1,49 |
| Поливиниловый спирт | 1,49 – 1,53 |
| Фенолформальдегидный полимер | 1,50 – 1,70 |
| Полиизобутилен | 1,51 |
| Полиэтилен | 1,51 |
| Натуральный каучук (полиизопрен) | 1,519 |
| Синтетический каучук (полиизопрен) | 1,522 |
| Полибутадиен | 1,520 |
| Полиамид | 1,54 |
| Поливинилхлорид (ПВХ) | 1,54 – 1,56 |
| Полистирол | 1,59 – 1,60 |
| Поливинилиденхлорид | 1,60 – 1,63 |
В табл. 7 приведены значения коэффициентов аморфной (nам ) и кристаллической (nкр ) фаз хлоропренового каучука в зависимости от температуры для образца, закристаллизованного при комнатной температуре (20 0 С).
Таблица 7 Значения коэффициентов nам и nкр в зависимости от температура образца
| Т, 0 С | nам | nкр | Т, 0 С | nам | nкр |
| −15 | 1,5698 | 1,6510 | 10 | 1,5623 | 1,6510 |
| −10 | 1,5678 | 1,6510 | 15 | 1,5587 | 1,6508 |
| −5 | 1,5659 | 1,6510 | 20 | 1,5571 | 1,6485 |
| 0 | 1,5641 | 1,6510 | 25 | 1,5550 | 1,6435 |
| 5 | 1,5623 | 1,6510 | 30 | 1,5533 | 1,6321 |
На основании представленных данных можно вычислить степень кристаллизации (φ) хлоропренового каучука по уравнению:
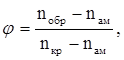
где nобр показатель преломления образца при определённой температуре.
Заключение
Список использованной литературы
1. Минкин В.И., Осипов О.А., Жданов Ю.А. Дипольные моменты в органической химии: М.: Химия, 1968. – 246 с.
2. Боровиков Ю.А. Диюэлектрометрия в органической химии: Киев: Наукова думка, 1987. – 215 с.
3. Бацанов С.С. Структурная рефрактометрия: Изд-во Московского ун-та, 1959. – 223 с.
4. Шишловский А.А. Прикладная физическая оптика,. ФизматГИЗ, 1970. – 822 с.
5. Ляликов Ю.С. Физико–химические методы анализа, М.: Химия, 1964.
6. Барановский В.Ф., Горелкин С.М., Городенцева В.А. Физико – химические методы анализа: М.: Высшая школа, 1972.
7. Рабек Я. Экспериментальные методы в химии полимеров: М.: Мир, 1983. Ч. 1. – 382 с.
8. Новикова Г.Е., Трапезникова О.Н. // Каучук и резина, 1968. – № 8.
9. Пиотровский К.Б., Стерензат Д.Е. // Каучук и резина, 1957. – № 11.
10. Пилипенко А.Т., Пятницкий И.В. Аналитическая химия; М.: Химия, 1990.
11. Практикум по физической химии под ред. Н.К. Воробьева; М.: Химия, 1975. – 367 с.
12. Иоффе Б.В. Рефрактометрические методы анализа в химии; Л.: Химия
13. Уитли П. Определение молекулярной структуры; М.: Мир, 1970.
14. Методические указания. Рефрактометрия. Лабораторная работа № 1. Волгоград. Изд-во ВПИ, 1983. – 14 с.
15. Краткий справочник физико–химических величин под редакцией К.П Мищенко: М.: Химия, 1967.
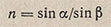






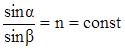 (1)
(1)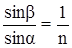 (2)
(2)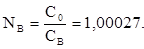 (3)
(3)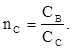 (4)
(4)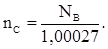 (5)
(5)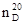 ,
,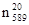 ). Верхний индекс показывает температуру (в 0 С), а нижний индекс – линии или длину волны (в нм), при которых производилось измерение. Обычно n определяют при указанных в табл. 1 длинах волн.
). Верхний индекс показывает температуру (в 0 С), а нижний индекс – линии или длину волны (в нм), при которых производилось измерение. Обычно n определяют при указанных в табл. 1 длинах волн.