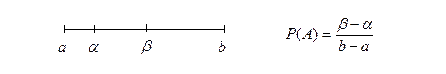Регистр калькулятора содержит 8 разрядов считая что появление любого числа

Определить вероятности того, что регистр содержит ровно две одинаковые цифры; регистр содержит ровно две пары одинаковых цифр

Регистр калькулятора содержит 8 разрядов. Считая, что появление любого числа равновероятно, определить вероятности следующих событий: C = <регистр содержит ровно две одинаковые цифры>, D = <регистр содержит ровно две пары одинаковых цифр>.

Хочу узнать, правильно ли моё решение?

P(C) = (10*10*9*8*7*6*5*4) / 10^8 ≈ 0,06
P(D) = (10*10*9*9*8*7*6*5) / 10^8 ≈ 0,14

Определить вероятность того, что наугад выбранное 4-хзначное число имеет ровно две пары одинаковых цифр
Определить вероятность того, что наугад выбранное четырехзначное число имеет ровно две пары.

Установить, что число содержит ровно две разные цифры
Буду премного благодарен за помощь. Натуральное число называется двояким, если в его десятичной.

Определить, верно ли, что заданное натуральное число содержит ровно три одинаковые цифры
Решите задачу дано натуральное число n n 10000 определить, верно ли, что это число содержит ровно.

Известно, что строка содержит ровно две одинаковые буквы. Найдите эти буквы
Всем привет. Мне нужна помощь, пожалуйста! Дана строка. Известно, что она содержит ровно две.

Дана строка. Известно, что она содержит ровно две одинаковые буквы. Найдите эти буквы
Дана строка. Известно, что она содержит ровно две одинаковые буквы. Найдите эти буквы.

Определить что число содержит две одинаковых цифры
Напишите программу которая определяет верно что введенное число содержит две одинаковых цифры что.

Верно ли, что число содержит ровно три одинаковые цифры?
Верно ли, что это число содержит ровно три одинаковые цифры, как, например, числа 6676, 4544, 0006.

Верно ли что число содержит ровно три одинаковые цифры
Пусть x четырехзначное число, верно ли что оно содержит ровно три одинаковые цифры.

Источник

Задачи и вопросы для уроков

Задачи и вопросы для уроков

1. На шахматную доску случайным образом ставят две ладьи – белую и черную. Какова вероятность того, что ладьи не побьют друг друга?

2. Из полного набора домино (28 штук) наудачу выбирают 7 костей. Какова вероятность того, что среди них окажется по крайней мере одна кость с шестью очками?

3. Наудачу выбирается пятизначное число. Какова вероятность, что оно: а) одинаково читается как слева направо, так и справа налево; b) состоит из нечетных цифр; c) четное?

4. Среди кандидатов на предстоящую конференцию студентов 3 первокурсника, 5 второкурсников и 7 третьекурсников. Из этого состава наудачу выбирают 5 человек. Какова вероятность того, что: а) будут выбраны одни третьекурсники; b) все первокурсники попадут на конференцию; с) не будет выбрано ни одного второкурсника?

5. Из колоды карт (их 36) наугад вынимают 2 карты. Найти вероятность, что среди них окажется хотя бы одна дама.

6. Из колоды карт (их 36) наудачу вынимают 5 карт. Найти вероятность того, что будут вытащены 2 туза и 3 шестерки?

7. Из колоды в 52 карты извлекаются наудачу 4 карты. Найти вероятность того, что: а) в полученной выборке все карты бубновой масти; b) окажется хотя бы один туз.

8. Из пяти карточек, на которых написаны цифры от 1 до 5, случайно выбирают три карточки и раскладывают их в порядке поступления в ряд слева направо. Найти вероятность того, что появится: а) число 123; b) число, не содержащее цифры 5; с) число, состоящее из последовательных цифр; d) четное число; e) число, содержащее хотя бы одну из цифр 2 или 3.

9. Колоду из 36 карт поделили случайным образом на две равные части. Найти вероятность того, что: а) в каждой половине по 2 дамы; b) в одной половине одна дама, а в другой – 3; c) все 4 дамы в одной части колоды.

10. За круглый стол случайным образом рассаживают 10 человек, найти вероятность того, что два фиксированных лица окажутся рядом.

11. Семь человек рассаживаются наудачу на скамейке. Какова вероятность того, что два определенных человека будут сидеть рядом?

12. 5 мужчин и 5 женщин случайным образом рассаживаются в ряд на 10 мест. Найти вероятность того, что: а) никакие два мужчины не будут сидеть рядом; b) все женщины будут сидеть рядом.

13. Регистр калькулятора содержит 8 разрядов. Считая, что появление любого числа на регистре равновероятно, найти вероятность того, что: а) во всех разрядах стоят нули; b) во всех разрядах стоят одни и те же числа; с) регистр содержит ровно две одинаковые цифры.

14. Парадокс де Мере. Подбрасывают три игральные кости и подсчитывают сумму выпавших очков. Де Мере заметил, что появление одиннадцати очков возможно при шести комбинациях (6-4-1, 6-3-2, 5-5-1, 5-4-2, 5-3-3, 4-4-3) и появление двенадцати очков возможно при шести комбинациях (6-5-1, 6-4-2, 6-3-3, 5-5-2, 5-4-3, 4-4-4). Объяснить парадоксальность ситуации, которая состоит в том, что вероятности появления в сумме 11 и 12 очков не равны.

15. В лифт 9-этажного дома вошли 4 человека. Каждый из них независимо друг от друга может выйти на любом (начиная со второго) этаже. Какова вероятность того, что: а) все вышли на разных этажах; b) все вышли на одном этаже; c) все вышли на 9 этаже; d) на втором, третьем и четвертом этажах не выйдет ни одного человека; e) двое выйдут на восьмом этаже?

16. Двенадцать студентов, среди которых Иванов и Петров, случайным образом занимают очередь в столовой. Какова вероятность, что между Ивановым и Петровым в образовавшейся очереди окажутся ровно 5 человек?

17. Числа 1, 2, 3, …, 9 записаны в случайном порядке. Найти вероятности того, что: а) числа записаны в порядке возрастания; b) числа 1 и 9 стоят рядом и в порядке возрастания; с) на четных местах стоят четные числа; d) сумма каждых двух чисел, стоящих на одинаковом расстоянии от концов равна 10.

18. На 5 карточках разрезной азбуки изображены буквы Е, Е, Л, П, П. Какова вероятность того, что при случайном выкладывании этих букв в ряд получится слово ПЕПЕЛ?

19. Из разрезной азбуки выкладывается слово МАТЕМАТИКА. Затем все буквы этого слова тщательно перемешиваются и снова выкладываются в случайном порядке. Какова вероятность того, что снова получится слово МАТЕМАТИКА?

20. Бросается 6 игральных костей. Найти вероятность того, что: а) выпадут 3 единицы, две тройки и одна пятерка; b) выпадут различные цифры; с) выпадут три одинаковые цифры.

21. Из 60 вопросов, входящих в экзаменационные билеты, студент знает 50. Найти вероятность того, что среди трех наугад выбранных вопросов студент знает: а) все вопросы; b) два вопроса.

.22. В кондитерской имеется 7 видов пирожков. Покупатель выбил чек на 4 пирожка. Считая, что любой заказываемый набор пирожков равновероятен, вычислить вероятность того, что покупатель заказал: а) пирожки одного вида; b) пирожки разных видов; c) по два пирожка различных видов.

23. Бросается 10 одинаковых игральных костей. Вычислить вероятность того, что ровно на двух костях выпадет 6 очков.

24. При проведении фуршета на стол поставили пять бокалов шампанского, три бокала белого вина и два бокала красного вина. К столу подошли семь человек и взяли по одному бокалу. Найти вероятность того, что на столе осталось по одному бокалу каждого напитка. (Будем предполагать, что для каждого из гостей все напитки одинаково привлекательны).

25. На заводе работает 30000 рабочих и служащих. Показать, что на данном заводе обязательно найдутся хотя бы два человека с одинаковыми инициалами фамилии, имени и отчества.

26. В коробке 6 синих, 4 красных и 3 зеленых карандаша. Наудачу вынимают 2 карандаша. Какова вероятность того, что все они разных цветов?

27. Из множества чисел <1, 2, …, 100>выбирается два числа. Какова вероятность того, что второе число больше первого, если выбор осуществляется без возвращения?

28. На отрезке [0,5] случайно выбирается точка. Найти вероятность того, что расстояние от нее до правого конца отрезка не превосходит 1,6 единиц.

29. Стержень длины l разломан в двух наугад выбранных точках. Найти вероятность того, что из полученных отрезков можно составить треугольник.

30. (Задача о встрече) Два студента условились встретиться в определенном месте между 14 и 15 часами дня. Пришедший первым ждет второго в течении 10 минут, после чего уходит. Какова вероятность, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода?

32. Вероятность попасть в самолет равна 0,4, а вероятность его сбить равна 0,1. Найти вероятность того, что при попадании в самолет он будет сбит.

33. В семье двое детей. Считая, что рождение мальчика и девочки – независимые и равновероятные события, вычислить вероятность того, что оба ребенка – мальчики, если известно, что в семье есть мальчик.

35. В группе учатся 10 студентов. Для решения задачи у доски любого из них могут вызвать с равной вероятностью один раз в течение занятия. В группе три отличника. Найти вероятность того, что вторую задачу к доске пойдет решать отличник, при условии, что первую задачу тоже решал отличник.

36. Бросается игральная кость. Пусть событие А = <появление четного числа очков>, событие В = <появление более трех очков>. Зависимы или нет события А и В?

38. Пусть Р(А) = 1/2, P(B) = 1/3. Верно ли, что ?

39. События А и В независимы, Р(А) = Р(В) = 1/4. Найти .

40. будет больше в случае А и В независимых или А и В несовместных?

41. Из колоды карт (36 карт) подряд вытаскиваются две карты. Рассматриваются события: А = <первая карта имеет пиковую масть>, В = <обе карты красного цвета>. Зависимы ли события А и В?

42. В ящике имеются две партии по 100 деталей, в каждой из которых по 10 бракованных деталей. Из ящика извлечена одна деталь. Зависимы ли случайные события А = <извлеченная деталь из первой партии>и В =<извлеченная деталь бракованная>?

43. В ящике имеются две партии по 100 деталей. В первой партии – 10 бракованных деталей, во второй – 20 бракованных. Из ящика извлечена одна деталь. Зависимы ли случайные события А = <извлеченная деталь из первой партии>и В = <извлеченная деталь бракованная>?

44. В группе из 1 000 человек 452 имеют текущие счета, 336 – депозитные счета, а 302 – и текущие, и депозитные. Определить, являются ли события <обладание текущим счётом>и <обладание депозитным счётом>независимыми?

Ответы

37. Зависимы; 38. Верно; 39. 13/16; 40. В случае несовместных А и В;

41. Зависимы, несовместны; 42. Независимы; 43. Зависимы;

Источник

Регистр калькулятора содержит 12 разрядов?

Регистр калькулятора содержит 12 разрядов.

Считая, что появление числа на регистре равновероятно, определить вероятность того, что во всех разрядах стоят нули.

Событие «во всех разрядах нули» может появиться 1 раз и эквивалентно событию «на калькуляторе 0»

всего чисел от 0 до 100000000000 : 100 000 000 001 = &gt ; P = 1 / 100 000 000 001.

Какое число содержит 8 единиц 5 разряда и 4 единицы второго разряда?

Какое число содержит 8 единиц 5 разряда и 4 единицы второго разряда.

1)откуда начинается отсчет разрядов в числе?

1)откуда начинается отсчет разрядов в числе?

2)Во сколько раз каждый разряд больше предыдущего?

3)во сколько раз увеличится число, если справа приписать один нуль, два нуля, три нуля.

Запиши число у которого в разрядах сотен тысяч стоит цифра 4 в разряде десятков тысяч стоит число 0 а в разряде едениц тысяч цифра 2 а во всех остальных разрядов цифра 3?

Запиши число у которого в разрядах сотен тысяч стоит цифра 4 в разряде десятков тысяч стоит число 0 а в разряде едениц тысяч цифра 2 а во всех остальных разрядов цифра 3.

ПОМОГИТЕ?

Для числа 6355670881320 запишите :

б) какая цифра стоит в разряде десятков тысяч ;

в) в каких разрядах стоит цифра 5.

Запиши все двузначные числа у которых число единиц на три меньше чем число десятков в разряде десятков стоит цифра пять в разряде единиц стоит цифра девять число десятков на один больше чем число един?

Запиши все двузначные числа у которых число единиц на три меньше чем число десятков в разряде десятков стоит цифра пять в разряде единиц стоит цифра девять число десятков на один больше чем число единиц и число единиц равных нулю.

Какое число содержит 8 единиц 5 разряда и 4 единицы второго разряда?

Какое число содержит 8 единиц 5 разряда и 4 единицы второго разряда?

Какое число содержит 4 единицы 6 разряда и 5 единиц 3 разряда?

Какое число содержит 4 единицы 6 разряда и 5 единиц 3 разряда.

Сколько единиц первого рязряда второго разряда третьего разряда четвертого разряда содержиться в числе 2002?

Сколько единиц первого рязряда второго разряда третьего разряда четвертого разряда содержиться в числе 2002.

Для числа 3755761881725 запишите : a) старший разряд ; б)какая цифра стоит в разряде десятков тысяч ; в) в каких разрядах стоит цифра 7?

Для числа 3755761881725 запишите : a) старший разряд ; б)какая цифра стоит в разряде десятков тысяч ; в) в каких разрядах стоит цифра 7.

Для числа 6355670881320 запишите а) старший разряд б) какая цифра стоит в разряде десятков тысяч в) в каких разрядах стоит цифра 5?

Для числа 6355670881320 запишите а) старший разряд б) какая цифра стоит в разряде десятков тысяч в) в каких разрядах стоит цифра 5.

Объём ящика 1м ^ 3 Объём одной коробки = 25 * 20 * 4 см ^ 3 = 2000 cм ^ 3 = 0, 002 м ^ 3 1 / 0, 002 = 500 Ответ : влезет 500 коробок.

25 / 100 = 1 / 4 / это деление это как бы легко)).

Применены : формула сложения, формула преобразования суммы в произведение, табличное значение косинуса.

Источник

Регистр калькулятора содержит 8 разрядов считая что появление любого числа

Стоимость готового решения каждой задачи 30руб

В назначении перевода укажите номера задач

ТВ637 Из партии, содержащей 10 изделий, среди которых 3 бракованных, наудачу извлекают три изделия для контроля. Найти вероятности следующих событий: А = <в полученной выборке содержится хотя бы одно бракованное изделие>, В = <в полученной выборке все изделия бракованные>, С = <в полученной вы-борке ровно 2 бракованных изделия>.

ТВ639 Среди кандидатов в студенческий совет факультета 3 первокурсника, 5 второ-курсников и 7 третьекурсников. Из этого состава наудачу выбирают пять че-ловек на пред¬стоящую конференцию. Найти вероятности следующих событий: А = <будут выбраны одни третьекурсники>, В = <все первокурсники попадут на конференцию>, С = <не будет выбрано ни одного второкурсника>, D = <будет выбран следующий состав: 1 первокурсник, 2 второкурсника и 2 третьекурсника>.

ТВ642 В группе 10 девушек и 8 юношей. Случайно отобраны 12 человек. Найти ве-роятность того, что среди них окажутся: 1) 4 девушки, 2) 3 юноши, 3) 6 деву-шек, 4) 8 юношей.

ТВ637 На пяти карточках написаны цифры от 1 до 5. Опыт состоит в случайном выборе трех карточек и раскладывании их в порядке поступления в ряд слева направо. Найти вероятности следующих событий: А=<появится число 123>, В=<появится число, не содержащее цифры 3>, С=<появится число, состоящее из последовательных цифр>, D=<появится четное число>, Е =<появится число, содер¬жащее хотя бы одну из цифр 2 или 3>.

ТВ643 Устройство состоит из 7 элементов, из которых 4 изношены. При включении устройства включаются случайным образом 3 элемента. Найти вероятность того, что случайно включёнными окажутся неизношенные элементы.

ТВ644 В кондитерской имеется 7 видов пирожных. Оче¬редной покупатель выбил чек на 4 пирожных. Считая, что любой заказываемый набор пирожных равноверо-ятен, вы¬числить вероятность того, что покупатель заказал: а) пирожные одно-го вида, б) пирожные разных видов, в) по два пирожных различных видов.

ТВ646 Бросается 10 одинаковых игральных костей. Вычислить вероятности следую-щих событий: А = <ни на одной кости не выпадет 6 очков>, В = <хотя бы на одной кости выпадет 6 очков>, С = <ровно на 3 костях выпадет 6 очков>.

ТВ647 Телефонная книга раскрывается наудачу и выбирается случайный номер телефона. Считая, что телефонные номера состоят из 7 цифр, причем все ком-бинации цифр равновероятны, найти вероятности следующих событий: А=<четыре последние цифры телефонного номера одинаковы>, В=<все цифры различны>, С=<номер начинается с цифры 5>, D=<номер содержит три цифры 5, две цифры 1, две цифры 2>.

ТВ648 Шесть пассажиров поднимаются на лифте 9-этажного дома. Считая, что дви-жение лифта начинается с первого этажа, найти вероятности следующих собы-тий: А = <на первых трех этажах не выйдет ни один из пассажиров>, В = <все пассажиры выйдут на первых шести этажах>, С = <на пятом, шестом и седьмом этажах выйдут по два пассажира>, D = <все пассажиры выйдут на одном этаже>.

ТВ651 Из разрезной азбуки выкладывается слово «мате¬матика». Затем все буквы этого слова тщательно перемеши¬ваются и снова выкладываются в случайном порядке. Ка¬кова вероятность того, что снова получится слово «мате¬матика»?

ТВ652 В лотерее выпущено п билетов, из которых т выигрышные. Куплено k билетов. Какова вероятность следую¬щих событий: А=<из k билетов хотя бы один выигрышный>, В=<из k билетов ровно один выигрышный>, С=<из k билетов ровно k1 выигрышных>?

ТВ654 7 яблок, 3 апельсина и 5 лимонов раскладываются случайным образом в три пакета, но так, чтобы в каждом было одинаковое количество фруктов. Найти вероятности следующих событий: А=<в каждом из пакетов по одному апель-сину>, В=<случайно выбранный пакет не содержит апельсинов>.

ТВ655 Из партии, содержащей 15 изделий, среди которых 5 бракованных, наудачу извлекают три изделия для конт¬роля. Найти вероятности следующих событий: А=<в полученной выборке содержится только одно бракованное изделие>, В=<в полученной выборке нет ни одного бракованного изделия>, С=<в полу-ченной выборке ровно 2 бракованных изделия>.

ТВ656 В группе 8 девушек и 5 юношей. Случайно отобраны 6 человек. Найти веро-ятность того, что среди них окажутся: 1) 3 девушки, 2) 4 юноша, 3) 6 девушек, 4) 6 юношей.

ТВ657 Устройство состоит из пяти элементов, из которых два изношены. При вклю-чении устройства включаются случайным образом два элемента. Найти веро-ятность того, что включёнными окажутся неизношенные элементы.

ТВ658 Брошены две игральные кости. Найти вероятности следующих событий: а) сумма выпавших очков равна семи; б) сумма выпавших очков равна восьми, а разность четырем; в) сумма выпавших очков равна восьми, если известно, что их разность равна четырем; г) сумма выпавших очков равна пяти, а произведение четырем.

ТВ660 В группе 12 студентов, среди которых 8 отличников. По списку наудачу ото-браны 9 студентов. Найти вероятность того, что среди отобранных студентов пять отличников.

ТВ661 В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных 11 изделий окажутся: а) одно окрашенное изделие; б) два окрашенных изде-лия; в) хотя бы одно окрашенное изделие.

ТВ662 В «секретном» замке на общей оси четыре диска, каждый из которых разделен на пять секторов, на которых написаны различные цифры. Замок открывается только в том случае, если диски установлены так, что цифры на них состав-ляют определенное четырехзначное число. Найти вероятность того, что при произвольной установке дисков замок будет открыт.

ТВ663 из 20 студентов 8 имеют спортивные разряды. Какова вероятность того, что выбранные наудачу 5 студентов имеют спортивные разряды.

ТВ664 По условиям лотереи “Спортлото 6 из 45” участник лотереи. Угадавший 4, 5, 6 видов из отобранных при случайном розыгрыше 6 видов спорта из 45, полу-чает денежный приз. Найти вероятность того, что будут угаданы: 1) все 6 цифр, 2) 4 цифры.

Источник

Решение типовых задач

Задача 1. На 5 карточках разрезной азбуки написаны буквы п, р, с, о, т. Перемешанные карточки вынимаются наудачу по одной и располагаются в одну линию. Какова вероятность прочесть слово «спорт»?

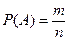
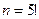
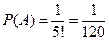
Решение. Искомую вероятность события А (можно прочесть слово «спорт») определим по формуле . Здесь общее число всевозможных исходов – число перестановок из 5 элементов. Благоприятствующим исходам отвечает одно слово «спорт», т. е. . Таким образом, .

Задача 2. Из 9 карточек, занумерованных разными цифрами, выбираются наудачу 3. Найти вероятность того, что последовательная запись их номеров показывает возрастание.

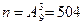
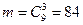
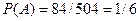
Решение. Трехзначные числа – упорядоченные тройки элементов из 9 цифр – есть размещения из 9 по 3, т.е. . Число благоприятных исходов . Следовательно, искомая вероятность .

Задача 3. Среди 17 студентов группы, в которой 9 юношей, производится розыгрыш 7 билетов лотереи, причем каждый студент может выбрать только один билет. Какова вероятность того, что среди обладателей билетов будет 4 девушки?

Решение. Обозначим событие А – среди 7 обладателей билетов будет 4 девушки. Количество равновозможных способов выбора по 7 человек из 17 равно .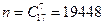

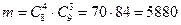
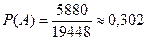
Число благоприятных исходов, т. е. число выборок по 7, в которых 4 девушки сочетаются с 3 юношами, определяется по правилу произведения . Тогда искомая вероятность .

Задача 4. В секцию магазина поступило 10 велосипедов, из которых 4 – с дефектами. Наудачу взяты 3. Найти вероятность того, что среди взятых будут: а) все без дефектов; б) все одинакового качества.

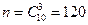
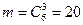
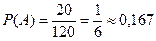
Решение. а) Событие А – все 3 наудачу взятые из 10 велосипедов без дефектов. Число возможных исходов . Три велосипеда без дефектов можно выбрать из 6 имеющихся способами. Искомая вероятность .

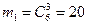
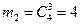
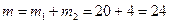
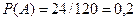
б) Событие В – все 3 велосипеда одного качества, т.е. или 3 годные, или 3 с дефектами. Три годные из 6 можно выбрать способами, а 3 с дефектами из 4 имеющихся способами. Общее число способов выбора 3-х велосипедов одинакового качества по правилу суммы равно . Следовательно, .

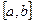
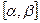
Задача 5.Тонкую иглу (точку) бросают на отрезок . Какая вероятность того, что она попадет на отрезок ?

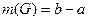
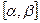
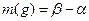
Решение. По условию игламожет упасть в любую точку указанного отрезка. В данном случае перечислитьвсе точки отрезка невозможно. Воспользуемся геометрическим определением и в качестве меры выберем длину отрезка . Интересующему нас событию благоприятствует ситуация, когда игла упадет в любую точку отрезка . Тогда .

Задачи для отчета преподавателю

А 1.1.На 6 карточках написаны буквы к, а, р, е, т, а. После того, как их тщательно перемешают, берут наудачу по 1 карточке и кладут последовательно рядом. Какова вероятность того, что получится слово «ракета»?

А 1.2.Из разрезной азбуки выкладывается слово «статистика». Затем все буквы этого слова перемешиваются и снова выкладываются в случайном порядке. Какова вероятность того, что снова получится слово «статистика»?

А 1.3.Из разрезной азбуки составлено слово «треугольник». Ребенок, не умеющий читать, рассыпал эти буквы, а затем выбрал 4 из них и собрал в произвольном порядке. Найти вероятность того, что у него появятся слова: а) «руль»; б) «угол».

А 1.4.Телефонный номер состоит из 7 цифр. Какова вероятность того, что в нем: а) все цифры различны; б) все цифры нечетные; в) все цифры различны и четные?

А 1.5.По линии связи в случайном порядке передаются 30 знаков алфавита. Найти вероятность того, что на ленте появится последовательность букв, образующих слово «режим».

А 1.6.Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что они различны, набрал эти цифры наудачу. Какова вероятность того, что набран нужный номер?

А 1.7.В лифт семиэтажного дома на первом этаже вошли 3 человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со 2-го. Найти вероятность следующих событий: а) все пассажиры выйдут на 4-м этаже; б) все пассажиры выйдут одновременно (на одном и том же этаже); в) все пассажиры выйдут на разных этажах.

А 1.8.В коробке содержится 4 одинаковых занумерованных кубика. Наудачу по одному извлекают все кубики из коробки. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.

А 1.9.Наудачу выбирается пятизначное число. Какова вероятность следующих событий: а) число одинаково читается как слева направо, так и справа налево (например, 12321); б) число кратно 5; в) число состоит из нечетных цифр.

А 1.10.На понедельник в институте запланировано 3 лекции по различным предметам из 10 изучаемых на данном курсе. Какова вероятность того, что студент, не успевший ознакомиться с расписанием, его угадает, если любое расписание из 3 предметов равновозможно?

А 1.11.Из полного набора домино (28 штук) наудачу выбирают 7 костей. Какова вероятность, что среди них окажется: а) по крайней мере одна кость с 5 очками; б) по крайней мере одна кость с 5 или 6 очками?

А 1.12.Из 10 первых букв русского алфавита наудачу составляется новый алфавит, состоящий из 5 букв. Определить вероятность следующих событий: а) в состав нового алфавита входит буква «а»; б) в состав нового алфавита входят только согласные буквы.

А 1.13.Среди кандидатов в студсовет факультета 3 первокурс­ника, 5 второкурсников и 7 третьекурсников. Из этого состава наудачу выбирают 5 человек на конференцию. Найти вероятность следующих событий: а) будут выбраны одни третьекурсники; б) все первокурсники попадут на конференцию; в) не будет выбрано ни одного второкурсника.

А 1.14. Из колоды в 52 карты извлекаются наудачу 4 карты. Найти вероятность следующих событий: а) выбраны все карты трефовой масти; б) выбран хотя бы один король.

А 1.15. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равно­возможно в течение данных суток. Определить вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода – 1 час, а второго – 3 часа.

А 1.16.На отдельных карточках написаны 12 вариантов контрольной работы, которые распределяются случайным образом среди 10 студентов, сидящих в одном ряду. Найти вероятность следующих событий: а) варианты с номерами 4 и 5 останутся неиспользованными; б) варианты 5 и 10 достанутся рядом сидящим студентам; в) будут распределены последовательные номера вариантов.

А 1.17.Среди 10 студентов, случайным образом занимающих очередь за учебниками в библиотеку, находятся 2 подруги. Какова вероятность того, что в образовавшейся очереди между подругами окажется 4 человека?

А 1.18.Из общего количества костей домино наудачу извлекли 1 кость. Оказалось, что это не дубль. Какова вероятность того, что 2-ю извлеченную кость домино можно будет приставить к 1-й?

А 1.19.В подъезде дома установлен замок с кодом. Дверь автоматически отпирается, если последовательно набрать 2 цифры из имеющихся 10. Некто вошел в подъезд и, не зная кода, стал пробовать различные комбинации, затрачивая на каждую попытку 10 секунд. Какова вероятность того, что вошедшему удастся открыть дверь: а) за 10 минут; б) за 15 минут; в) за 1 час?

А 1.20.В телефонной книге случайно выбирается номер телефона, состоящий из 7 цифр. Найти вероятность того, что: а) четыре последние цифры телефонного номера одинаковы; б) все четыре последние цифры различны.

А 1.21.В ящике имеется 15 деталей, 9 из которых окрашены. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что извлеченные детали окрашены.

А 1.22.Группа из 8 юношей и 8 девушек делится случайно на 2 равные части. Найти вероятность того, что в каждой части юношей и девушек поровну.

А 1.23.Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков будет равна 8, а разность – 4.

А 1.24.На 5 карточках написаны цифры 1, 2, 3, 4, 5. Две из них одна за другой извлекаются. Найти вероятность того, что число на 2-й карточке будет больше, чем на 1-й.

А 1.25.Программа экзамена содержит 20 различных вопросов, из которых студент знает только 10. Для успешной сдачи экзамена достаточно ответить на 2 из 3 предложенных вопросов. Какова вероятность успешной сдачи экзамена?

А 1.26.Студент знает 20 из 25 вопросов программы. Зачет считается сданным, если студент ответит не менее чем на 3 из 4 вопросов билета. Взглянув на 1-й вопрос билета, студент обнаружил, что он его знает. Какова вероятность того, что студент: а) сдаст зачет; б) не сдаст зачет?

А 1.27.В лотерее 100 билетов. Из них 25 выигрышных. Определить вероятность того, что 2 приобретенных билета окажутся выигрышными.

А 1.28.Регистр калькулятора содержит 8 разрядов. Считая, что появление любого числа на регистре случайно, определить вероятность следующих событий: а) во всех разрядах стоят нули; б) во всех разрядах стоят одни и те же цифры; в) регистр содержит только 2 одинаковые цифры; г) регистр содержит только 2 пары одинаковых цифр; д) регистр содержит 3 одинаковые цифры.

А 1.29.Из 7 яблок, 3 апельсинов и 5 лимонов случайным образом в пакет отбирают 5 фруктов. Найти вероятности следующих событий: а) в пакете только 1 апельсин; б) пакет не содержит апельсинов; в) пакет не содержит лимонов; г) пакет не содержит яблок.

А 1.30.Путем жеребьевки разыгрываются 6 подписных изданий среди 12 участников, каждый из которых не может получить более 1 подписки. Найти вероятность того, что из списка получат подписку: а) первые 6 человек; б) первые 3 человека; в) 1-й человек; г) 1-й и 3-й человек.

А 1.31.Подбрасывают наудачу 3 игральные кости. Вычислить вероятности следующих событий: а) на 3 костях выпадут разные грани; б) хотя бы на одной из костей выпадет шестерка.

А 1.32.В ящике лежат 12 красных, 8 зеленых и 10 синих карандашей. Наудачу вынимаются без возвращения 2 карандаша. Найти вероятность того, что окажется не вынутым: а) синий карандаш; б) зеленый карандаш; в) красный карандаш.

А 1.33.Студент знает 14 вопросов из 20. В билете 3 вопроса. Найти вероятность того, что студент ответит хотя бы на один из них.

А 1.34.В круг вписан квадрат. Найти вероятность того, что точка, брошенная наудачу в круг, окажется внутри квадрата.

А 1.35.На шахматной доске случайным образом поставлены черная и белая ладьи. Какова вероятность того, что они не могут бить друг друга?

А 1.36.При наборе телефонного номера абонент забыл две последние цифры и набрал их наудачу, помня только, что эти цифры нечетные и разные. Найти вероятность того, что номер набран правильно.

А 1.37.На карточках отдельно написаны буквы: А – на 3;
Е – на 1-й; И – на 1-й; К – на 1-й; М – на 2; Т – на 2 карточках.
Ребенок берет карточки в случайном порядке и прикладывает их одну к другой. Найти вероятность того, что в результате получится слово «МАТЕМАТИКА».

А 1.38.10 солдат-новобранцев разного роста случайным образом становятся в строй. Какова вероятность того, что они расположатся в строю по росту?

А 1.39.Среди поступающих в ремонт часов 40% нуждаются в общей чистке механизма. Какова вероятность того, что из 5 взятых наугад часов все нуждаются в чистке механизма?

А 1.40.Из 20 сбербанков 10 расположены за чертой города. Для аудиторской проверки случайно выбраны 5 сбербанков. Какова вероятность того, что хотя бы 2 из них окажутся в черте города?

В 1.1.В механизм входят три одинаковые детали. Работа механизма нарушается, если при его сборке будут поставлены все три детали размера, больше обозначенного на чертеже. У сборщика пять деталей из оставшихся 12 большего размера. Найти вероятность: а) нормальной; б) ненормальной работы первого собранного из этих деталей механизма, если сборщик берет детали наудачу.

В 1.4.Слово «ИНТЕГРАЛ» состоит из букв разрезной азбуки. Наудачу извлекают 4 карточки и выкладывают в ряд друг за другом в порядке появления. Какова вероятность того, что при этом получится слово «ИГРА»?

В 1.5.Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы «А», «Г», «И», «Л», «М», «О», «Р», «Т», получится слово «АЛГОРИТМ»?

В 1.6.Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы «О», «О», «О», «Л», «М», «Т», «К», получится слово «МОЛОТОК»?

В 1.7.Из пяти видов открыток наудачу выбираются 3 открытки. Какова вероятность того, что все три открытки будут разные?

В 1.8.На 5 одинаковых шарах написаны числа 1, 2, 3, 4, 5 – по одному на каждом. Шары положены в урну и перемешаны. Какова вероятность того, что, вынимая наудачу один за другим 3 шара, (без возврата) получим все 3 шара нечетного номера?

В 1.9.В группе учится 12 человек, из них 10 юношей и 2 девушки. На субботник отбирают 5 человек. Какова вероятность того, что в субботнике будут участвовать обе девушки?

В 1.10.Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.

В 1.11.Найти вероятность того, что точка, брошенная в произвольное место внутри круга радиуса R=5, попадет во вписанный в этот круг правильный треугольник.

В 1.12.Найти вероятность того, что точка, брошенная в произвольное место внутри круга радиуса R=6, попадет во вписанный в этот круг квадрат.

В 1.13.Найти вероятность того, что точка, брошенная в произвольное место внутри круга радиуса R=2, попадет во вписанный в этот круг прямоугольный равнобедренный треугольник.

В 1.14.В круг радиуса 10 см бросают точку. Найти вероятность того, что расстояние от этой точки до центра круга не превышает 5 см.

В 1.15.В круг радиуса 20 см бросают точку. Найти вероятность того, что расстояние от этой точки до центра круга больше 5 см.

В 1.16.В круг радиуса 12 см бросают точку. Найти вероятность того, что расстояние от этой точки до центра круга заключено в пределах от 2 до 5 см.

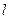
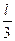
В 1.17.Стержень длиной разломали на две части. Найти вероятность того, что длина меньшей части не превысит .

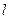
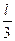
В 1.18.Стержень длиной разломали на две части. Найти вероятность того, что длина меньшей части превысит .

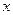
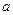
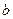
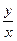
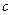
С 1Наудачу выбраны два положительных числа и , каждое из которых не превышает . Найти вероятность того, что их сумма будет не больше , а отношение – не меньше .

Номер варианта	Исходные данные	Номер варианта	Исходные данные
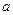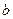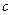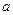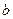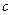С 1.1	С 1.16	1/2
С 1.2	С 1.17
С 1.3	1/2	С 1.18
С 1.4	С 1.19	3/4
С 1.5	1/3	С 1.20	1/3
С 1.6	С 1.21
С 1.7	С 1.22
С 1.8	С 1.23
С 1.9	С 1.24
С 1.10	1/2	С 1.25
С 1.11	1/4	С 1.26	1/2
С 1.12	С 1.27	1/2
С 1.13	С 1.28	1/2
С 1.14	С 1.29
С 1.15	С 1.30

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник