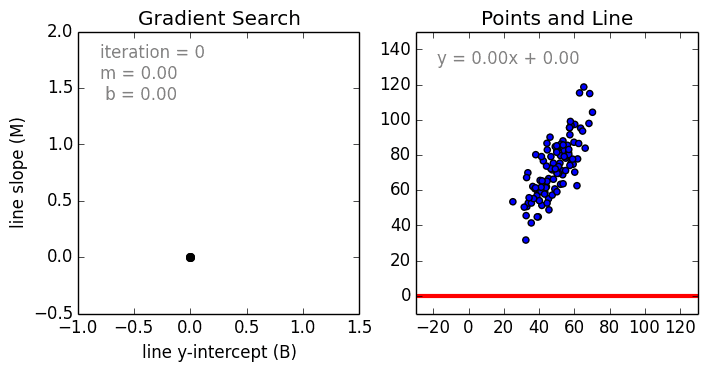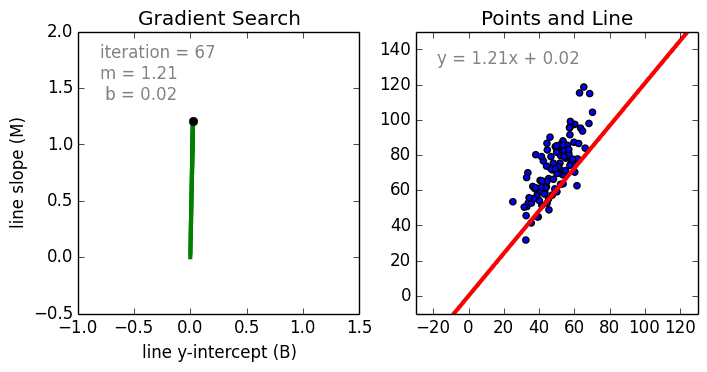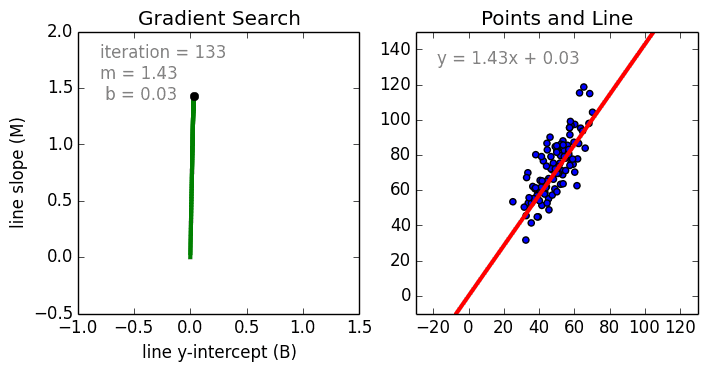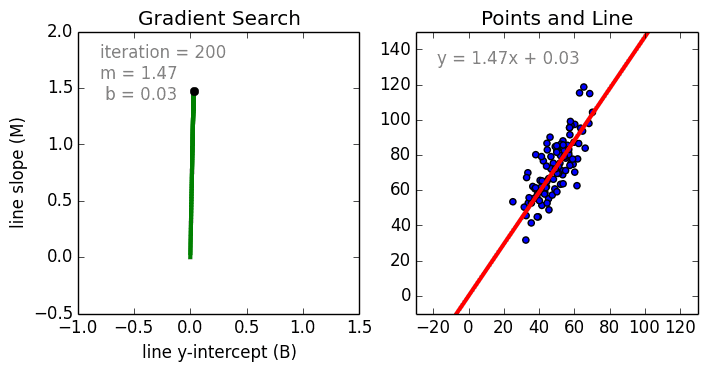
Регрессия что это в математике

Регрессия (математика)

Этот термин в статистике впервые был использован Френсисом Гальтоном (1886) в связи с исследованием вопросов наследования физических характеристик человека. В качестве одной из характеристик был взят рост человека; при этом было обнаружено, что в целом сыновья высоких отцов, что не удивительно, оказались более высокими, чем сыновья отцов с низким ростом. Более интересным было то, что разброс в росте сыновей был меньшим, чем разброс в росте отцов. Так проявлялась тенденция возвращения роста сыновей к среднему (regression to mediocrity), то есть «регресс». Этот факт был продемонстрирован вычислением среднего роста сыновей отцов, рост которых равен 56 дюймам, вычислением среднего роста сыновей отцов, рост которых равен 58 дюймам, и т. д. После этого результаты были изображены на плоскости, по оси ординат которой откладывались значения среднего роста сыновей, а по оси абсцисс — значения среднего роста отцов. Точки (приближённо) легли на прямую с положительным углом наклона меньше 45°; важно, что регрессия была линейной.

Итак, допустим, имеется выборка из двумерного распределения пары случайных переменных (X, Y). Прямая линия в плоскости (x, y) была выборочным аналогом функции

В этом примере регрессия Y на X является линейной функцией. Если регрессия Y на X отлична от линейной, то приведённые уравнения суть линейная аппроксимация истинного уравнения регрессии.

Простым примером регрессии Y по X является зависимость между Y и X, которая выражается соотношением: Y=u(X)+ε, где u(x)=E(Y | X=x), а случайные величины X и ε независимы. Это представление полезно, когда планируется эксперимент для изучения функциональной связи y=u(x) между неслучайными величинами y и x. На практике обычно коэффициенты регрессии в уравнении y=u(x) неизвестны и их оценивают по экспериментальным данным.

Линейная регрессия (пропедевтика)

Представим зависимость y от x в виде линейной модели первого порядка:

где означает предсказанное моделью значение y при данном x, b₀ и b₁ — выборочные оценки параметров модели, а — значения ошибок аппроксимации.

Метод наименьших квадратов даёт следующие формулы для вычисления параметров данной модели и их отклонений:

здесь средние значения определяются как обычно: , и s_e 2 обозначает остаточное отклонение регрессии, которое является оценкой дисперсии σ 2 в том случае, если модель верна.

Стандартные ошибки коэффициентов регрессии используются аналогично стандартной ошибке среднего — для нахождения доверительных интервалов и проверки гипотез. Используем, например, критерий Стьюдента для проверки гипотезы о равенстве коэффициента регрессии нулю, то есть о его незначимости для модели. Статистика Стьюдента: t=b/s_b. Если вероятность для полученного значения и n−2 степеней свободы достаточно мала, например, ,

а её стандартной ошибки

Обычно истинные величины коэффициентов регрессии β₀ и β₁ не известны. Известны только их оценки b₀ и b₁. Иначе говоря истинная прямая регрессии может пройти иначе, чем построенная по выборочным данным. Можно вычислить доверительную область для линии регрессии. При любом значении x соответствующие значения y распределены нормально. Средним является значение уравнения регрессии . Неопределённость его оценки характеризуется стандартной ошибкой регрессии:

Теперь можно вычислить 100(1−α/2)-процентный доверительный интервал для значения уравнения регрессии в точке x:

,

где t_{(1−α/2, n−2)} — t-значение распределения Стьюдента. На рисунке показана линия регрессии, построенная по 10 точкам (сплошные точки), а также 95%-я доверительная область линии регрессии, которая ограничена пунктирными линиями. С 95%-й вероятностью можно утверждать, что истинная линия находится где-то внутри этой области. Или иначе, если мы соберём аналогичные наборы данных (обозначены кружками) и построим по ним линии регрессии (обозначены голубым цветом), то в 95 случаях из 100 эти прямые не покинут пределов доверительной области. (Для визуализации кликните по картинке) Обратите внимание, что некоторые точки оказались вне доверительной области. Это совершенно естественно, поскольку речь идёт о доверительной области линии регрессии, а не самих значений. Разброс значений складывается из разброса значений вокруг линии регрессии и неопределённости положения самой этой линии, а именно:

Здесь m — кратность измерения y при данном x. И 100(1−α/2)-процентный доверительный интервал (интервал прогноза) для среднего из m значений y будет:

.

На рисунке эта 95%-я доверительная область при m=1 ограничена сплошными линиями. В эту область попадает 95 % всех возможных значений величины y в исследованном диапазоне значений x.

Источник

5 видов регрессии и их свойства

Jan 16, 2019 · 5 min read

Линейная и логистическая регрессии обычно являются первыми видами регрессии, которые изучают в таких областях, как машинное обучение и наука о данных. Оба метода считаются эффективными, так как их легко понять и использовать. Однако, такая простота также имеет несколько недостатков, и во многих случаях лучше выбирать другую регрессионную модель. Существует множество видов регрессии, каждый из которых имеет свои достоинства и недостатки.

Мы познакомимся с 7 наиболее распростран е нными алгоритмами регрессии и опишем их свойства. Также мы узнаем, в каких ситуация и с какими видами данных лучше использовать тот или иной алгоритм. В конце мы расскажем о некоторых инструментах для построения регрессии и поможем лучше разобраться в регрессионных моделях в целом!

Линейная регрессия

Регрессия — это метод, используемый для моделирования и анализа отношений между переменными, а также для того, чтобы увидеть, как эти переменные вместе влияют на получение определенного результата. Линейная регрессия относится к такому виду регрессионной модели, который состоит из взаимосвязанных переменных. Начнем с простого. Парная (простая) линейная регрессия — это модель, позволяющая моделировать взаимосвязь между значениями одной входной независимой и одной выходной зависимой переменными с помощью линейной модели, например, прямой.

Более распространенной моделью является множественная линейная регрессия, которая предполагает установление линейной зависимости между множеством входных независимых и одной выходной зависимой переменных. Такая модель остается линейной по той причине, что выход является линейной комбинацией входных переменных. Мы можем построить модель множественной линейной регрессии следующим образом:

Y = a_1*X_1 + a_2*X_2 + a_3*X_3 ……. a_n*X_n + b

Несколько важных пунктов о линейной регрессии:

Полиномиальная регрессия

Для создания такой модели, которая подойдет для нелинейно разделяемых данных, можно использовать полиномиальную регрессию. В данном методе проводится кривая линия, зависимая от точек плоскости. В полиномиальной регрессии степень некоторых независимых переменных превышает 1. Например, получится что-то подобное:

Y = a_1*X_1 + (a_2)²*X_2 + (a_3)⁴*X_3 ……. a_n*X_n + b

У некоторых переменных есть степень, у других — нет. Также можно выбрать определенную степень для каждой переменной, но для этого необходимы определенные знания о том, как входные данные связаны с выходными. Сравните линейную и полиномиальную регрессии ниже.

Несколько важных пунктов о полиномиальной регрессии:

Гребневая (ридж) регрессия

В случае высокой коллинеарности переменных стандартная линейная и полиномиальная регрессии становятся неэффективными. Коллинеарность — это отношение независимых переменных, близкое к линейному. Наличие высокой коллинеарности можно определить несколькими путями:

Сначала можно посмотреть на функцию оптимизации стандартной линейной регрессии для лучшего понимания того, как может помочь гребневая регрессия:

Где X — это матрица переменных, w — веса, y — достоверные данные. Гребневая регрессия — это корректирующая мера для снижения коллинеарности среди предикторных переменных в регрессионной модели. Коллинеарность — это явление, в котором одна переменная во множественной регрессионной модели может быть предсказано линейно, исходя из остальных свойств со значительной степенью точности. Таким образом, из-за высокой корреляции переменных, конечная регрессионная модель сведена к минимальным пределам приближенного значения, то есть она обладает высокой дисперсией.

Гребневая регрессия добавляет небольшой фактор квадратичного смещения для уменьшения дисперсии:

Такой фактор смещения выводит коэффициенты переменных из строгих ограничений, вводя в модель небольшое смещение, но при этом значительно снижая дисперсию.

Несколько важных пунктов о гребневой регрессии:

Регрессия по методу «лассо»

В регрессии лассо, как и в гребневой, мы добавляем условие смещения в функцию оптимизации для того, чтобы уменьшить коллинеарность и, следовательно, дисперсию модели. Но вместо квадратичного смещения, мы используем смещение абсолютного значения:

Существует несколько различий между гребневой регрессией и лассо, которые восстанавливают различия в свойствах регуляризаций L2 и L1:

Регрессия «эластичная сеть»

Эластичная сеть — это гибрид методов регрессии лассо и гребневой регрессии. Она использует как L1, так и L2 регуляризации, учитывая эффективность обоих методов.

min || Xw — y ||² + z_1|| w || + z_2|| w ||²

Практическим преимуществом использования регрессии лассо и гребневой регрессии является то, что это позволяет эластичной сети наследовать некоторую стабильность гребневой регрессии при вращении.

Несколько важных пунктов о регрессии эластичной сети:

Вывод

Вот и все! 5 распространенных видов регрессии и их свойства. Все данные методы регуляризации регрессии (лассо, гребневая и эластичной сети) хорошо функционирует при высокой размерности и мультиколлинеарности среди переменных в наборе данных.

Источник

R — значит регрессия

Статистика в последнее время получила мощную PR поддержку со стороны более новых и шумных дисциплин — Машинного Обучения и Больших Данных. Тем, кто стремится оседлать эту волну необходимо подружится с уравнениями регрессии. Желательно при этом не только усвоить 2-3 приемчика и сдать экзамен, а уметь решать проблемы из повседневной жизни: найти зависимость между переменными, а в идеале — уметь отличить сигнал от шума.

Для этой цели мы будем использовать язык программирования и среду разработки R, который как нельзя лучше приспособлен к таким задачам. Заодно, проверим от чего зависят рейтинг Хабрапоста на статистике собственных статей.

Введение в регрессионный анализ

Основу регрессионного анализа составляет метод наименьших квадратов (МНК), в соответствии с которым в качестве уравнения регресии берется функция такая, что сумма квадратов разностей минимальна.

Карл Гаусс открыл, или точнее воссоздал, МНК в возрасте 18 лет, однако впервые результаты были опубликованы Лежандром в 1805 г. По непроверенным данным метод был известен еще в древнем Китае, откуда он перекочевал в Японию и только затем попал в Европу. Европейцы не стали делать из этого секрета и успешно запустили в производство, обнаружив с его помощью траекторию карликовой планеты Церес в 1801 г.

Вид функции , как правило, определен заранее, а с помощью МНК подбираются оптимальные значения неизвестных параметров. Метрикой рассеяния значений вокруг регрессии является дисперсия.

Линейная регрессия

Уравнения линейной регрессии можно записать в виде

В матричном виде это выгладит

Случайная величина может быть интерпретирована как сумма из двух слагаемых:

Ограничения линейной регрессии

Для того, чтобы использовать модель линейной регрессии необходимы некоторые допущения относительно распределения и свойств переменных.

Как обнаружить, что перечисленные выше условия не соблюдены? Ну, во первых довольно часто это видно невооруженным глазом на графике.

Неоднородность дисперсии

При возрастании дисперсии с ростом независимой переменной имеем график в форме воронки.

Нелинейную регрессии в некоторых случая также модно увидеть на графике довольно наглядно.

Тем не менее есть и вполне строгие формальные способы определить соблюдены ли условия линейной регрессии, или нарушены.

В этой формуле — коэффициент взаимной детерминации между и остальными факторами. Если хотя бы один из VIF-ов > 10, вполне резонно предположить наличие мультиколлинеарности.

Почему нам так важно соблюдение всех выше перечисленных условий? Все дело в Теореме Гаусса-Маркова, согласно которой оценка МНК является точной и эффективной лишь при соблюдении этих ограничений.

Как преодолеть эти ограничения

Нарушения одной или нескольких ограничений еще не приговор.

К сожалению, не все нарушения условий и дефекты линейной регрессии можно устранить с помощью натурального логарифма. Если имеет место автокорреляция возмущений к примеру, то лучше отступить на шаг назад и построить новую и лучшую модель.

Линейная регрессия плюсов на Хабре

Итак, довольно теоретического багажа и можно строить саму модель.
Мне давно было любопытно от чего зависит та самая зелененькая цифра, что указывает на рейтинг поста на Хабре. Собрав всю доступную статистику собственных постов, я решил прогнать ее через модель линейно регрессии.

Загружает данные из tsv файла.

Вопреки моим ожиданиям наибольшая отдача не от количества просмотров статьи, а от комментариев и публикаций в социальных сетях. Я также полагал, что число просмотров и комментариев будет иметь более сильную корреляцию, однако зависимость вполне умеренная — нет надобности исключать ни одну из независимых переменных.

В первой строке мы задаем параметры линейной регрессии. Строка points

. определяет зависимую переменную points и все остальные переменные в качестве регрессоров. Можно определить одну единственную независимую переменную через points

Перейдем теперь к расшифровке полученных результатов.

Можно попытаться несколько улучшить модель, сглаживая нелинейные факторы: комментарии и посты в социальных сетях. Заменим значения переменных fb и comm их степенями.

Проверим значения параметров линейной регрессии.

Проверим, соблюдены ли условия применимости модели линейной регрессии? Тест Дарбина-Уотсона проверяет наличие автокорреляции возмущений.

И напоследок проверка неоднородности дисперсии с помощью теста Бройша-Пагана.

В заключение

Конечно наша модель линейной регрессии рейтинга Хабра-топиков получилось не самой удачной. Нам удалось объяснить не более, чем половину вариативности данных. Факторы надо чинить, чтобы избавляться от неоднородной дисперсии, с автокорреляцией тоже непонятно. Вообще данных маловато для сколь-нибудь серьезной оценки.

Но с другой стороны, это и хорошо. Иначе любой наспех написанный тролль-пост на Хабре автоматически набирал бы высокий рейтинг, а это к счастью не так.

Источник

Регрессия – что это такое простыми словами

Часто в математике, экономике и других отраслях деятельности можно встретить такой термин, как «регрессия». В переводе с латинского это слово означает «отступление», «возвращение».

В зависимости от контекста регрессия означает немного разные явления, однако есть общее сходство – практически всегда имеется в виду переход от прогресса в обратную сторону. Это спуск вниз, с верхней ступени развития к нижней.

Регрессия в психологии

В психоанализе применяется термин «регрессия», где таким образом маркируют возврат от более высокой ступени психологической организации к низкой. Например, в ходе психоаналитической сессии пациент может вернуться к предыдущим этапам своего эмоционального, сексуального развития, к более примитивным и упрощенным вариантам поведения, мышления, реагирования.

Регрессией называют и сам процесс движения психики пациента в новый формат. Иногда регрессия необходима как один из этапов преодоления комплексов, зависимости, раскрытия причин психотравм и душевных ран. Это необходимо для адаптации человека к переменам во внутреннем мире и внешней среде.

Психологическая регрессия может сопровождаться необычными фантазиями, детскими и примитивными желаниями. В регрессивной форме может проявляться либидо, отношение к родителям.

Наблюдается также регрессия поведения – это одна из форм защиты, когда человек внутренне уходит от реальности и неблагоприятных событий в действительности. Это временный, как правило, переходный вариант поведения, необходимый для адаптации. Так работает универсальный механизм встроенной защиты.

Человек возвращается на прошедшую стадию развития, чтобы облегчить собственное состояние, перенести разные по силе переживания.

Регрессия в математике

В математических науках регрессия применяется как относительная величина, отражающая зависимость среднего показателя какой-то величины от другой или нескольких величин. Такой может быть «множественная регрессия».

Линейной регрессией называют статистическую модель, отражающую зависимость одной переменной у от различных факторов – одного или нескольких. Такие факторы – независимые переменные – называются регрессорами. Через линейную регрессию можно восстановить зависимость между двумя любыми переменными.

Существует также криволинейная регрессия, где в уравнении прописываются изменения одной переменной у в качестве функции t для изменения в другой переменной – х. Это квадратное уравнение, бывает также кубическое или уравнение другого, более высокого порядка. В криволинейной регрессии отсутствуют постоянные коэффициенты, отражающие изменения между переменными.

В математических расчетах также применяются другие типы регрессий: одномерная, полиномиальная, логистическая, множественная.

Логистическая регрессия рассматривает случаи связей между разными двумя классами, позволяет вывести обоснования и минимизировать эмпирический риск. Этот метод применяется в так называемой байесовской классификации, в методах настройки весов.

При помощи логистической регрессии (она же логит-регрессия, логит-модель) предсказывают степень вероятности наступления разных событий. Результат подгоняется к логистической кривой с использованием полученных модельных данных.

Регрессия в статистике

Для точности результатов в статистике важна корректная постановка задачи – таким путем можно правильно восстановить структуру логит-модели. Выработка правильного алгоритма обеспечит отыскание правильных параметров.

В статистике применяется линейный дискриминант Фишера на основе логистической регрессии. Он основан на байесовских правилах (байесовская сеть). Применяется принцип максимального правдоподобия, но на практике достигаются очень разные результаты.

Другой метод математической статистики – множественная регрессия, которая является расширенной версией простого варианта регрессии. Этот метод позволяет прогнозировать действия одной переменной или ее критериев (измерения переменной).

Множественная регрессия используется для многомерного анализа, где наблюдаются взаимосвязи между зависимой переменной у и совокупности предикторов – независимых переменных х, расчет делается на базе линейного уравнения.

В виде регрессии обычно также представлен исходный код в основе компьютерной программы.

Морская регрессия

Так называемая «морская регрессия» характеризует период отлива – регулярного, обусловленного положением Луны на орбите, когда морские воды отступают от берегов.

Суша поднимается, опускается океаническое дно и в случае тектонических разломов, землетрясений.

В прошедшие эпохи геологические изменения регрессивного характера затрагивали целые материки – сокращался объем воды в океанах, менялись очертания берегов в ледниковый период.

Чаще всего регрессия моря – это уменьшение количества воды в Мировом океане в целом (как следствие массивного оледенения материков). При этом опускаются большие участки морского или океанического ложа, уровень и количество воды существенно падает.

Источник