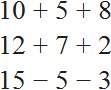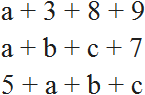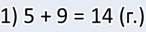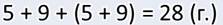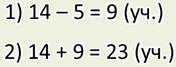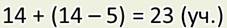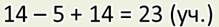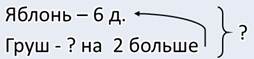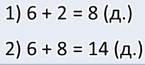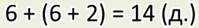Решить задачу выражением что это

Решить задачу выражением что это

СПОСОБЫ РЕШЕНИЯ ЗАДАЧ

Понятие “решение задачи” можно рассматривать с различных точек зрения: решение как результат, т.е. как ответ на вопрос, поставленный в задаче, и решение как процесс нахождения этого результата.

С точки зрения методики обучения решению задач на первый план выступает процесс нахождения результата, который в свою очередь, тоже можно рассматривать с различных точек зрения Во-первых, как способ нахождения результата и, во-вторых, как последовательность тех действий, который входят в тот или иной способ.

Восемь яблок разложили по 2 на несколько тарелок. Сколько понадобилось тарелок?

Учащиеся могут решить эту задачу, не имея никакого представления о делении и о записи этого действия, а только опираясь на свой жизненный опыт и владея счетом от 1 до 8. Для этого они отсчитывают 8 яблок, положат 2 на одну тарелку, затем 2 на другую и т.д. пока не разложат все. Посчитав количество тарелок, они ответят на поставленный вопрос. Такой способ и называется практическим или предметным. Его возможности ограничены, так как учащийся может выполнить предметные действия только с небольшим количеством предметов. Усвоив смысл действия деления и его запись, можно решить эту задачу уже не практическим, а арифметическим способом, записав равенство 8 : 2 = 4.

Задачи, в которых для ответа на вопрос нужно выполнить только одно действие, называются простыми. Если для ответа на вопрос задачи нужно выполнить два и более действий, то такие задачи называются составными. Составную задачу, так же как и простую можно решить, используя различные способы.

Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?

Обозначим каждую рыбу кругом. Нарисуем 10 кругов и обозначим

Для ответа на вопрос задачи можно не выполнять арифметические действия, так как количество пойманных щук соответствует тем кругам, которые не обозначены (их З).

Для ответа на вопрос задачи мы выполнили два действия.

Тогда количество всех рыб можно записать выражением:

По условию задачи известно, что рыбак поймал всего 10 рыб.

Значит 3 + 4 + х = 10

Решив это уравнение, мы ответим на вопрос задачи.

Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.

В начальных классах используются различные формы записи решения задач по действиям, по действиям с пояснением, с вопросами, выражением.

У мальчика было 90 книг. 28 он поставил на первую полку, 12 на вторую. Остальные на третью. Сколько книг на третьей пилке?

а) решение по действиям

Ответ: 50 книг на третьей полке.

б) по действиям с пояснением

1) 28 + 12 = 40 (к.) на 1 и 2 полках вместе.

1) Сколько книг на первой и второй полках вместе?

2) Сколько книг на третьей полке?

При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:

Не следует путать такие понятие как: решение задачи различными способами (практический, арифметический графический, алгебраический), различные формы записи арифметического способа, решения задачи (по действиям, выражением по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомым, а, с следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.

Например, рассмотренную выше задачу можно решить другим арифметическим способом:

В качестве арифметического способа можно рассматривать и такое решение данной задачи:

В числе способов решения задач ложно назвать схематическое моделирование. В отличие от графического способа, который позволяет ответить на вопрос задачи, используя счет и присчитывание схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство) Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить не вопрос задачи.

Когда из гаража выехало 18 машин, в нем осталось в 3 раза меньше, чем было. Сколько машин было в гараже?

Решение этой задачи арифметическим способом довольно сложно для ребенка. Но если использовать схему, то от нее легко перейти к записи арифметического действия. В этом случае запись решения будет иметь вид:

Ответ: 27 машин было в гараже

В альбоме для раскрашивания 48 листов. Часть альбома Коля раскрасил. Сколько листов осталось не раскрашенными, если Коля раскрасил в 2 раза больше, чем ему осталось?

Решение задачи можно оформить так:

48 : 3 = 16 (л.) Ответ: 16 листов

[../../../_private/navbar1.htm]

Источник

Выражения

Выражение — это любое сочетание чисел, букв и знаков операций. Можно сказать, что вся математика состоит из выражений.

Выражения бывают двух видов: числовые и буквенные.

Числовые выражения состоят из чисел и знаков математических операций. Например, следующие выражения являются числовыми:

Буквенные выражения помимо чисел и знаков операций содержат ещё и буквы. Например, следующие выражения являются буквенными:

Буквы, которые содержатся в буквенных выражениях, называются переменными. Запомните это раз и навсегда! Спросите любого школьника что такое переменная — этот вопрос поставит его в ступор, несмотря на то что он будет решать сложные задачи по математике, не зная что это такое. А между тем, переменная это фундаментальное понятие, без понимания которого математику невозможно изучать.

Под словом «изучать» мы подразумеваем самостоятельное чтение соответствующей литературы и способность понимать, что там написано. А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.

Поскольку понятие переменной очень важно, остановимся на нём подробнее. Посмотрите внимательно на слово «переменная». Ничего не напоминает? Слово «переменная» происходит от слов «меняться», «изменить», «изменить своё значение». Переменная в математике всегда выражена какой-то буквой. Например, запишем следующее выражение:

Значение переменной a подставляется в исходное выражение.

В результате имеем: 5 + 5 = 10

Конечно, мы рассмотрели простейшее выражение. На практике встречаются более сложные выражения, в которых присутствуют дроби, степени, корни и скобки. Выглядит это устрашающе. На самом деле ничего страшного. Главное понять сам принцип.

Значение переменной x подставляется в выражение x + 10

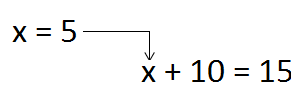
Переменная это своего рода контейнер, где хранится значение. Переменные удобны тем, что они позволяют, не приводя примеров доказывать теоремы, записывать различные формулы и законы.

Имея выражение a + b = c, можно пользоваться им, подставляя вместо переменных a и b любые числа. А переменная c будет получать своё значение автоматически, в зависимости от того, какие числа будут подставлены вместо a и b

Решение:

Значение выражения

Фраза « выполнить действие » означает выполнить одну из операций действия.

Значение выражения — это результат выполнения действий, содержащихся в выражении.

Рассмотрим еще примеры:

Источник

Математика. 2 класс

Конспект урока

Математика, 2 класс

Урок № 22. Решение текстовых задач. Запись решения выражением

Перечень вопросов, рассматриваемых в теме:

— Что такое встречное движение, расстояние?

— Как выполнять схематический чертёж к задачам на движение?

Задача – это упражнение, которое выполняется посредством умозаключения, вычисления.

Выражение – формула, выражающая какие–либо математические отношения.

Расстояние – пространственный промежуток, разделяющий два объекта, отрезок пути.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

Теоретический материал для самостоятельного изучения

Расстояние – это путь, который прошёл какой-либо объект.

РАССТОЯНИЕ – промежуток в пространстве, разделяющий два объекта

Измеряя расстояние, мы будем использовать сокращённые записи.

Сегодня на уроке мы будем решать новые задачи – задачи на движение.

Длина аллеи 80 м. Два мальчика пошли навстречу друг другу. Один прошёл до встречи 45 м. Сколько прошёл до встречи другой мальчик?

Сделаем к задаче схематический чертёж.

Начертим отрезок, обозначающий длину всей дорожки, или расстояние между концами дорожки. Синей стрелкой обозначим длину дорожки. Укажем – 80 метров.

Мальчики шли навстречу друг другу с разных сторон дорожки. На чертеже это будем обозначать стрелками, которые показывают направление движения каждого мальчика.

Место встречи мальчиков будем обозначать флажком.

Теперь обозначим, что один мальчик прошёл до встречи 45 метров, а другой –

неизвестно. Поставим знак вопроса.

Так выглядит схематический чертёж к задаче. По чертежу видно, что нам необходимо найти разность отрезков, выполнить вычитание.

Чтобы узнать, сколько метров до встречи прошёл второй мальчик, вычтем из длины всей дорожки длину пути, который прошёл первый мальчик.

80 – 45 = 35 (м) прошёл второй мальчик.

Второй мальчик прошёл до встречи 35 метров.

Решим вторую задачу:

Девочки измеряли длину дорожки с двух концов, идя навстречу друг другу. Одна девочка прошла до встречи 30 м, другая на 4 метра меньше. Какой длины была дорожка?

Сделаем схематический чертёж к задаче.

Итак, нам надо найти длину всей дорожки. Для этого мы должны знать, сколько метров прошла каждая девочка. Мы знаем, сколько прошла первая девочка – 30 метров. А сколько прошла вторая девочка, нам надо узнать.

Будем решать задачу в два действия. Запишем первое действие:

1) 30 – 4 = 26 (м) прошла вторая девочка.

Вторая девочка прошла до встречи двадцать шесть метров.

Теперь можем ответить на вопрос задачи. Запишем второе действие:

2) 30 + 26 = 56 (м) длина дорожки.

Длина всей дорожки была 56 метров.

Вывод: Для решения задач на движение обычно выполняют чертёж, в котором стрелками показывают направление движения объектов. Движение может быть встречным или в противоположных направлениях.

1.Подберите схематический чертёж к задаче

Красная Шапочка отправилась в гости к бабушке. До дома бабушки нужно пройти 100 метров. Красная Шапочка уже прошла 70 метров. Сколько ей осталось пройти?

2.Соедините каждый чертёж с карточкой, на которой записано соответствующее решение задачи.

30 – 20

30 + 20

70 – 45

70 – 45

30 + 20

30 – 20

Источник

Запись решения задачи выражением

Урок 15. Математика 2 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Запись решения задачи выражением»

— Плюс. Плююююс! Ты где?

Привет, Плюс! Чего так долго? Включай скорее компьютер. Сейчас у нас будет в скайпе разговор с царицей Математикой.

— Здравствуй, Минус. Как это я забыл! Включаю.

— Здравствуйте, Дорогие Плюс и Минус!

— Да, царица, мы Вас внимательно слушаем.

— Мы очень внимательно слушаем.

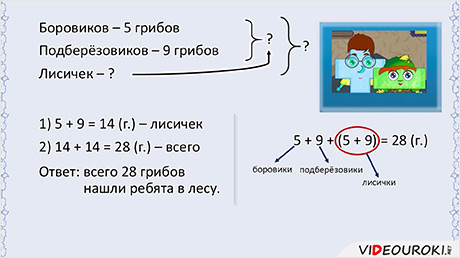
— Ну что же, приступим. Итак, вот первая задача:

Ну, Плюс и Минус, я жду вашего решения. Может быть и ребята, которые на вас смотрят, попробуют решить эту задачу.

— Всё, я готов! Могу даже объяснить, как я решал эту задачу.

В задаче два неизвестных, значит, задача составная, то есть в ней не одно действие, а два. В первом действии я узнаю, сколько лисичек.

А так как боровиков и подберёзовиков вместе столько же, сколько и лисичек, то общее количество грибов я нашёл вот так:

Ответ: всего 28 грибов нашли ребята в лесу.

— А я решал задачу другим способом. Вот посмотрите:

— Ну что же, начинаем решать. Ребята, и вы попробуйте с нами решать!

— Я уже решил. Вот посмотрите, в задаче известно количество мальчиков, Их 14. Но неизвестно количество девочек. Ведь сказано, что их на 5 меньше, чем мальчиков.

Ответ: всего 23 учащихся присутствовало на уроке физкультуры.

— А вот я записал решение этой задачи по-другому:

И ещё можно вот так:

Ты первым действием узнаёшь, сколько девочек, и я тоже. Ведь это действие я записал в скобках. А то, что записано в скобках, всегда выполняется первым.

— Ты, Плюс, как всегда. Все тебе надо складывать да экономить. Хотя, наверное, ты прав. Эта запись действительно удобная. А хотелось бы и мне попробовать такую запись задачи выражением.

Ваше величество, госпожа королева. Не могли бы Вы задать нам ещё одну задачу?

— Ну что же, слушайте:

В моём саду растёт 6 яблонь. А груш на 2больше. Сколько всего яблонь и груш растёт в моём саду?

— Ну вот что у меня получилось. Прежде, чем узнать, сколько всего яблонь и груш, необходимо узнать, сколько груш. Ведь нам это неизвестно. Сказано, что их на 2 больше, чем яблонь.

Значит, в саду царицы растёт 14 яблонь и груш.

А вот как получилась запись выражением:

— Хорошо. Задача решена, верно. А теперь расскажите, чему вы научились.

— Можно я начну первый.

Записывать решение задачи можно по действиям и выражением.

— При записи по действиям мы пишем номер действия и пояснения к каждому действию, а при записи выражением только пояснение к значению записанного выражения.

— При записи выражения первое действие часто записываем в скобках, и конечно, не забываем записать ответ задачи.

— Ну что же, молодцы, Плюс и Минус. Вы справились с заданием. И сейчас вы можете пойти погулять в мой сад и полакомиться яблоками и грушами.

Источник

Урок «Решение задач выражением»

Тем а: РЕШЕНИЕ ЗАДАЧ И ВЫРАЖЕНИЙ

Педагогические задачи: продолжать работу над задачами и выражениями изученных видов; нормировать умение группировать слагаемые, находить удобный способ решения выражений; :отрабатывать умение находить периметр многоугольника; развивать логическое мышление, внимание, наблюдательность.

Планируемые образовательные результаты:

Личностные: принимают и осваивают социальную роль обучающегося; стремятся развивать внимание, память, логическое мышление, навыки сотрудничества со сверстниками и со взрослыми; проявляют самостоятельность, личную ответственность.

Предметные: знают: свойства сложения; устную и письменную нумерацию чисел в пределах 100; отличительные особенности задачи; что такое периметр многоугольника; умеют: применять свойства сложения для нахождения значения числового выражения; решать задачи изученных видов; соотносить задачу с данными чертежом и выражениями; составлять задачи, обратные данной; находить периметр треугольника.

Метапредметные (критерии сформированности оценки компонентов УУД): регулятивные : формулируют учебную задачу урока; контролируют в форме сличения способа действия его результата с заданным эталоном, при необходимости вносят корректировки; оценивают собственную деятельность и деятельность партнеров; способны к мобилизации волевых усилий; познавательные : формулируют познавательную цель, создают алгоритм деятельности; анализируют объекты с целью выделения существенных признаков, сравнивают их, строят логическую цепочку рассуждений, устанавливают причинно-следственные связи;

Методы и формы обучения : частично-поисковый; индивидуальная, фронтальная, групповая.

Образовательные ресурсы: http://www.fizkult-ura.ru/node/l 13, электронное приложение к учебнику « Математика 2 класс М.И.Моро и др.»

Оборудование: интерактивная доска, компьютер.

Наглядно-демонстрационный материал : кораблики для устного счета, кораблики из геометрических фигур, карта путешествий с паровозиком из Ромашково

Основные понятия и термины: сложение, свойства сложения, сложить, вычесть, слагаемое, сумма, значение суммы, уменьшаемое, вычитаемое, разность, значение разности, задача, простая задача, составная задача, чертеж, выражение, сравнить, периметр, многоугольник, треугольник.

Сядьте поудобнее, у нас разминка для ума.

«Проверяй не зевай – очень быстро отвечай».

Какой день недели предшествует субботе? (пятница)

Как называется емкость, в которой находится зубная паста? (тюбик)

У Иванушки –дурачка были три брата и три сестры. Сколько в семье мальчиков? (четыре)

Пассажир такси ехал в село. По дороге он встретил 5 грузовиков и 3 автомашины. Сколько всего машин шло в село? (одна машина – такси)

Бежали по дорожке два гуся, кошка, собачка. Сколько лапок топало той дорожкой по полю? (8 лапок)

В лесу жил в избушке смешной толстячок

С ним был неразлучен сосед – Пятачок.

Читал он вопилки приятелю вслух.

Скажите, кто он? (Винни-Пух)

Путешествовать по королевству математики мы отправимся с паровозиком из Ромашково. Вы помните мультфильм про паровозик из Ромашково?

3.Устный счёт…станция «Отвечай-ка»

Весёлые кораблики Соедини кораблики

В игрушечном порту Волшебною чертой

У каждого кораблика Ответом предыдущего

Примеры на борту Чтоб стал корабль другой.

2) Какое число пропущено?

На доске: несколько моделей часов, которые показывают разное время.

( Числа от 1 до 100сложение и вычитание

III. Сообщение темы и целей учебной деятельности.

— Сегодня на уроке вы будете совершенствовать умения: решать выражения, используя известные вам свойства сложения; решать задачи с опорой на схематический чертеж; решать геометрические задачи.

Тема сегодняшнего урока: «Решение задач и выражений».

А примеры-то, примеры
Ждут давно уж нас они
Их решайте побыстрее
Все мы будем молодцы!

— Рассмотрите выражения, записанные на доске:

14-9 6 + 7 19+ (9-8) 5 + 8

— Разделите выражения на группы так, чтобы в каждой группе оказались похожие выражения.

14-9 6 + 7 20-(2+ 8) 5 7-7+1

11-7 5 + 8 19 + (9-8) 7 6-6+1

— Найдите значения этих выражений. Третий и четвертый столбики выполните с подробным
объяснением.

Задания на смекалку и логическое мышление.

Электронное приложение « Воздушные шарики»

«Числовое выражение.» задание 2)

— Решите выражения из задания 1 (с. 46).
Желательно, чтобы выражения были записаны на доске.

— Применяя правило, с которым вы познакомились на прошлом уроке, найдите самый удобный способ решения выражений.

(Задание выполняется с комментированием.)

Удобно к семи прибавить три, а к семидесяти прибавить двадцать, после чего полученные результаты сложить. Сумма чисел 7 и 3 равна 10. Сумма чисел 70 и 20 равна 90. К девяноста прибавить 10- получим 100. Значение суммы чисел 7, 20, 3 и 70 равно 100. И т. д.

( Хлопки над головой в ладоши.)

(Повороты туловища влево-вправо.

Наклоны туловища влево-вправо.)

(Хлопки над головой в ладоши.

Машут руками как крыльями.)

(Хлопки над головой в ладоши.)

Вот под елочкой зеленой

Скачут весело вороны:

Целый день они кричали,

Спать ребятам не давали:

Только к ночи умолкают

И все вместе засыпают:

Прочитайте текст задачи 4 (с. 46) и соотнесите его со схемой-чертежом, приведенной ниже.

Что в задаче известно? Как это показано на чертеже?

Что требуется узнать? Как это показано на чертеже?

Запишите решение задачи. Сформулируйте и запишите ответ задачи.

Прочитайте задачу 5 (с. 46) и сопоставьте ее со схемой-чертежом.

Рассмотрите выражения, записанные ниже.

Что узнаем, если к 30 прибавим 20? (Число каменных домов.)

Что узнаем, решив второе выражение? (Сколько всего домов в дачном поселке.)

Какое из выражений является решением задачи? (Второе.)

Запишите его и решите. Дайте ответ на вопрос задачи.

VI. Работа с геометрическим материалом. Станция « Измеряй-ка».

Как называется фигура, изображенная на полях учебника (с. 46) (Треугольник.)

Что вы можете сказать о данном треугольнике?

(Все стороны треугольника имеют разную длину.)

Проверьте, правы ли вы, измерив стороны треугольника.

Найдите периметр данного треугольника. Проверьте работу друг друга.

VII. Задание по образцу.

Рассмотрите данный предмет –Что это? (кораблик)

-назовите геометрические фигуры, из которых состоит кораблик.

(3 треугольника и 1 квадрат)

-«Какой фигуры не хватает?».

VIII. Рефлексия учебной деятельности.

Чему научил вас урок?

Какое задание было для вас самым интересным?

А какое самым трудным?

Что помогло справиться с трудностями?

Подведение итогов урока-путешествия

Источник