Рядом фибоначчи называется последовательность найти матрицу а такую что

Записать в матрицу элементы ряда Фибоначчи (N*N)

Записать в массив К[20] элементы ряда Фибоначчи
Записать в массив К элементы ряда Фибоначчи.

Записать в файл те элементы массива, которые являются числами Фибоначчи
Написать программу, которая заполняет линейный массив, размер которого задается с клавиатуры.

Вывести на экран из n элемент ряда Фибоначчи-это элементы числовой последовательности
Вывести на экран из n элемент ряда Фибоначчи-это элементы числовой последовательности.

Диапазон индексов массива сделал тот же, что и у Вас.

Замечу, что, если быть точным, то у Вас применяется не ряд Фибоначчи (который начинается с чисел 1, 1), а ряд Фибоначчи, дополненый нулевым членом (начинается с чисел 0, 1).

Решение

Bluevaran, я так понимаю, на вопросы Вы будете затрудняться ответить. Поэтому отвечу за Вас.

1. Порядок обхода массивов с количеством измерений более 1 не декларирован. По этой причине порядок обхода элементов матрицы нужно в каждом конкретном случае оговаривать отдельно. И, раз уж Вам дали такую задачу, то Ваши преподаватель и составитель задачи (троечники, естественно) ничего об этом не подозревают. В каком порядке обходить матрицу? На самом деле, любой порядок обхода матрицы является допустимым («верным», «правильным»), главное, чтобы были просканированы все элементы по одному разу за полный обход. Предлагаю обходить матрицу в «естественном» порядке: слева-направо, сверху-вниз. Почему в «естественном» в кавычках? А это потому, например, что для китайцев и японцев такой порядок естественным не является. Ну да ладно. Короче, в Вашем случае нужно будет обходить матрицу, начиная с правого нижнего угла, справа-налево, снизу-вверх.

Последние три типа я привёл для справки, нас интересовать они не могут, так как в Pascal ABC их нет.

Получается, что максимальный размер матрицы для целочисленных типов данных, который может быть использован в программе, это 6*6.

Матрица может быть 1*1, ведь так?

Чтобы не париться с индексами двумерного массива, число Фибоначчи будем вычислять отдельно, а не на основании предыдущих чисел (уже сохранённых в массиве).

Можно, конечно, и 9*9 вывести, но 80 и 81 числа Фибоначчи в мантиссу типа real не помещаются, поэтому выводятся на печать с ошибкой в младших разрядах. Да и 78 число тоже со ошибкой выдаётся почему-то. Наверное, это накопленная ошибка, циклы всё-таки, лень выяснять. Но, если очень хотите, можете назначить m=9.

Если желаете, чтобы и нулевой член ряда Фибоначчи выводился, то замените строчки, идущие после until:

Источник

5 способов вычисления чисел Фибоначчи: реализация и сравнение

Введение

Программистам числа Фибоначчи должны уже поднадоесть. Примеры их вычисления используются везде. Всё от того, что эти числа предоставляют простейший пример рекурсии. А ещё они являются хорошим примером динамического программирования. Но надо ли вычислять их так в реальном проекте? Не надо. Ни рекурсия, ни динамическое программирование не являются идеальными вариантами. И не замкнутая формула, использующая числа с плавающей запятой. Сейчас я расскажу, как правильно. Но сначала пройдёмся по всем известным вариантам решения.

Код предназначен для Python 3, хотя должен идти и на Python 2.

Для начала – напомню определение:

Замкнутая формула

Решаем квадратное уравнение:

Откуда и растёт «золотое сечение» ϕ=(1+√5)/2. Подставив исходные значения и проделав ещё вычисления, мы получаем:

что и используем для вычисления F_n.

Хорошее:
Быстро и просто для малых n
Плохое:
Требуются операции с плавающей запятой. Для больших n потребуется большая точность.
Злое:
Использование комплексных чисел для вычисления F_n красиво с математической точки зрения, но уродливо — с компьютерной.

Рекурсия

Самое очевидное решение, которое вы уже много раз видели – скорее всего, в качестве примера того, что такое рекурсия. Повторю его ещё раз, для полноты. В Python её можно записать в одну строку:

Хорошее:
Очень простая реализация, повторяющая математическое определение
Плохое:
Экспоненциальное время выполнения. Для больших n очень медленно
Злое:
Переполнение стека

Запоминание

У решения с рекурсией есть большая проблема: пересекающиеся вычисления. Когда вызывается fib(n), то подсчитываются fib(n-1) и fib(n-2). Но когда считается fib(n-1), она снова независимо подсчитает fib(n-2) – то есть, fib(n-2) подсчитается дважды. Если продолжить рассуждения, будет видно, что fib(n-3) будет подсчитана трижды, и т.д. Слишком много пересечений.

Поэтому надо просто запоминать результаты, чтобы не подсчитывать их снова. Время и память у этого решения расходуются линейным образом. В решении я использую словарь, но можно было бы использовать и простой массив.

(В Python это можно также сделать при помощи декоратора, functools.lru_cache.)

Хорошее:
Просто превратить рекурсию в решение с запоминанием. Превращает экспоненциальное время выполнение в линейное, для чего тратит больше памяти.
Плохое:
Тратит много памяти
Злое:
Возможно переполнение стека, как и у рекурсии

Динамическое программирование

После решения с запоминанием становится понятно, что нам нужны не все предыдущие результаты, а только два последних. Кроме этого, вместо того, чтобы начинать с fib(n) и идти назад, можно начать с fib(0) и идти вперёд. У следующего кода линейное время выполнение, а использование памяти – фиксированное. На практике скорость решения будет ещё выше, поскольку тут отсутствуют рекурсивные вызовы функций и связанная с этим работа. И код выглядит проще.

Это решение часто приводится в качестве примера динамического программирования.

Хорошее:
Быстро работает для малых n, простой код
Плохое:
Всё ещё линейное время выполнения
Злое:
Да особо ничего.

Матричная алгебра

И, наконец, наименее освещаемое, но наиболее правильное решение, грамотно использующее как время, так и память. Его также можно расширить на любую гомогенную линейную последовательность. Идея в использовании матриц. Достаточно просто видеть, что

А обобщение этого говорит о том, что

Два значения для x, полученных нами ранее, из которых одно представляло собою золотое сечение, являются собственными значениями матрицы. Поэтому, ещё одним способом вывода замкнутой формулы является использование матричного уравнения и линейной алгебры.

Так чем же полезна такая формулировка? Тем, что возведение в степень можно произвести за логарифмическое время. Это делается через возведения в квадрат. Суть в том, что

где первое выражение используется для чётных A, второе для нечётных. Осталось только организовать перемножения матриц, и всё готово. Получается следующий код. Я организовал рекурсивную реализацию pow, поскольку её проще понять. Итеративную версию смотрите тут.

Хорошее:
Фиксированный объём памяти, логарифмическое время
Плохое:
Код посложнее
Злое:
Приходится работать с матрицами, хотя они не так уж и плохи

Сравнение быстродействия

Сравнивать стоит только вариант динамического программирования и матрицы. Если сравнивать их по количеству знаков в числе n, то получится, что матричное решение линейно, а решение с динамическим программированием – экспоненциально. Практический пример – вычисление fib(10 ** 6), числа, у которого будет больше двухсот тысяч знаков.

n = 10 ** 6
Вычисляем fib_matrix: у fib(n) всего 208988 цифр, расчёт занял 0.24993 секунд.
Вычисляем fib_dynamic: у fib(n) всего 208988 цифр, расчёт занял 11.83377 секунд.

Теоретические замечания

Не напрямую касаясь приведённого выше кода, данное замечание всё-таки имеет определённый интерес. Рассмотрим следующий граф:

Подсчитаем количество путей длины n от A до B. Например, для n = 1 у нас есть один путь, 1. Для n = 2 у нас опять есть один путь, 01. Для n = 3 у нас есть два пути, 001 и 101. Довольно просто можно показать, что количество путей длины n от А до В равно в точности F_n. Записав матрицу смежности для графа, мы получим такую же матрицу, которая была описана выше. Это известный результат из теории графов, что при заданной матрице смежности А, вхождения в А n — это количество путей длины n в графе (одна из задач, упоминавшихся в фильме «Умница Уилл Хантинг»).

Почему на рёбрах стоят такие обозначения? Оказывается, что при рассмотрении бесконечной последовательности символов на бесконечной в обе стороны последовательности путей на графе, вы получите нечто под названием «подсдвиги конечного типа», представляющее собой тип системы символической динамики. Конкретно этот подсдвиг конечного типа известен, как «сдвиг золотого сечения», и задаётся набором «запрещённых слов» <11>. Иными словами, мы получим бесконечные в обе стороны двоичные последовательности и никакие пары из них не будут смежными. Топологическая энтропия этой динамической системы равна золотому сечению ϕ. Интересно, как это число периодически появляется в разных областях математики.

Источник

Ряд Фибоначчи. Ключ. Матрица Золотого Сечения

В последнее время, работая в индивидуальных и групповых процессах с людьми, я возвращался к мыслям об объединении всех процессов (кармических, психических, физиологических, духовных, трансформационных и др.) в одно.

Друзья за завесой всё шире раскрывали образ многомерного Человека и взаимосвязи всего во всём.

Внутреннее побуждение подтолкнуло меня вернуться к старым исследованиям с цифрами и ещё раз просмотреть книгу Друнвало Мельхиседека «Древняя тайна цветка жизни».

В это время в кинотеатрах показывали фильм «Код да Винчи». Я не намерен обсуждать качество, ценность и истинность этого фильма. Но момент с кодом, когда цифры стали стремительно прокручиваться, стал для меня одним из ключевых в этом фильме.

Интуиция подсказывала мне о том, что стоит обратить внимание на числовую последовательность Фибоначчи и Золотое Сечение. Если вы заглянете в Интернет с целью найти что-нибудь о Фибоначчи, то на вас обрушится лавина информации. Вы узнаете, что об этой последовательности знали во все времена. Она представлена в природе и космосе, в технике и науке, в архитектуре и живописи, в музыке и пропорциях в теле человека, в ДНК и РНК. Многие исследователи этой последовательности пришли к мнению, что ключевые события в жизни человека, государства, цивилизации также подчинены закону золотого сечения.

Создаётся впечатление, что Человеку дана фундаментальная подсказка.

Тогда возникает мысль, что Человек осознанно может применить принцип Золотого Сечения для восстановления здоровья и коррекции судьбы, т.е. упорядочивания происходящих процессов в собственной вселенной, расширения Сознания, возвращения в Благосостояние.

Вместе вспомним последовательность Фибоначчи:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025…

Каждое последующее число образуется путём сложения двух предыдущих:

Теперь я предлагаю каждое число ряда привести к одной цифре: 1, 1, 2, 3, 5, 8,

13=1+3(4), 21=2+1(3), 34=3+4(7), 55=5+5(1), 89= 8+9(8), 144=1+4+4(9)…

Вот что у нас получилось:

1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9…1, 1, 2…

последовательность из 24 чисел, которая снова повторяется с 25-го:

Не кажется ли вам странным или закономерным, что

Если получившуюся последовательность записать следующим образом,

1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9

8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9

9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9,

то мы увидим, что 1-е и 13-е число последовательности, 2-е и 14-е,3-е и 15-е, 4-е и 16-е … 12-е и 24-е в сумме дают 9.

Теперь продвинемся дальше:

1 1 2 3 5 8 4 3 7 1 8 9 8 8 7 6 4 1 5 6 2 8 1 9

2 2 4 6 1 7 8 6 5 2 7 9 7 7 5 3 8 2 1 3 4 7 2 9

4 4 8 3 2 5 7 3 1 4 5 9 5 5 1 6 7 4 2 6 8 5 4 9

3 3 6 9 6 6 3 9

При тестировании этих числовых рядов у нас получился:

Матрица Золотого Сечения

1 1 2 3 5 8 4 3 7 1 8 9 8 8 7 6 4 1 5 6 2 8 1 9

1 1 2 3 5 8 4 3 7 1 8 9 8 8 7 6 4 1 5 6 2 8 1 9

2 2 4 6 1 7 8 6 5 2 7 9 7 7 5 3 8 2 1 3 4 7 2 9

3 3 6 9 6 6 3 9 3 3 6 9 6 6 3 9 3 3 6 9 6 6 3 9

5 5 1 6 7 4 2 6 8 5 4 9 4 4 8 3 2 5 7 3 1 4 5 9

8 8 7 6 4 1 5 6 2 8 1 9 1 1 2 3 5 8 4 3 7 1 8 9

4 4 8 3 2 5 7 3 1 4 5 9 5 5 1 6 7 4 2 6 8 5 4 9

3 3 6 9 6 6 3 9 3 3 6 9 6 6 3 9 3 3 6 9 6 6 3 9

7 7 5 3 8 2 1 3 4 7 2 9 2 2 4 6 1 7 8 6 5 2 7 9

1 1 2 3 5 8 4 3 7 1 8 9 8 8 7 6 4 1 5 6 2 8 1 9

8 8 7 6 4 1 5 6 2 8 1 9 1 1 2 3 5 8 4 3 7 1 8 9

9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9

8 8 7 6 4 1 5 6 2 8 1 9 1 1 2 3 5 8 4 3 7 1 8 9

8 8 7 6 4 1 5 6 2 8 1 9 1 1 2 3 5 8 4 3 7 1 8 9

7 7 5 3 8 2 1 3 4 7 2 9 2 2 4 6 1 7 8 6 5 2 7 9

6 6 3 9 3 3 6 9 6 6 3 9 3 3 6 9 6 6 3 9 3 3 6 9

4 4 8 3 2 5 7 3 1 4 5 9 5 5 1 6 7 4 2 6 8 5 4 9

1 1 2 3 5 8 4 3 7 1 8 9 8 8 7 6 4 1 5 6 2 8 1 9

5 5 1 6 7 4 2 6 8 5 4 9 4 4 8 3 2 5 7 3 1 4 5 9

6 6 3 9 3 3 6 9 6 6 3 9 3 3 6 9 6 6 3 9 3 3 6 9

2 2 4 6 1 7 8 6 5 2 7 9 7 7 5 3 8 2 1 3 4 7 2 9

8 8 7 6 4 1 5 6 2 8 1 9 1 1 2 3 5 8 4 3 7 1 8 9

1 1 2 3 5 8 4 3 7 1 8 9 8 8 7 6 4 1 5 6 2 8 1 9

9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9

Практическое применение ряда Фибоначчи

Один мой друг выразил намерение индивидуально поработать с ним на тему развития своих возможностей и способностей.

Неожиданно в самом начале в процесс пришёл Саи Баба и пригласил следовать за ним.

Мы стали подниматься вверх внутри Божественной Монады друга и, выйдя из неё через Причинное Тело, оказались в другой реальности на уровне Космического Дома.

Кто изучал труды Марка и Элизабет Клер Профетов, знают учение о Космических Часах, которое им передала Мать Мария.

На уровне Космического Дома Юрий увидел круг, обладающий внутренним центром с 12-ю стрелками.

Старец, который встретил нас на этом уровне, сказал, что перед нами Божественные Часы и 12-ть стрелок олицетворяют 12-ть (24) Проявлений Божественных Аспектов… (возможно Творцов).

Что касается Космических Часов, то они располагались под Божественными по принципу энергетической восьмёрки.

— В каком режиме по отношению к тебе находятся Божественные Часы?

— Стрелки у Часов стоят, нет движения. Ко мне приходят сейчас мысли о том, что много эонов лет назад я отказался от Божественного Сознания и пошёл другим путём, путём Мага. Все мои магические артефакты и амулеты, которые у меня и во мне скопились за множество воплощений, на этом уровне выглядят как детские погремушки. На тонком плане они представляют собой образ магических энергетических одежд.

— Если у тебя желание дальше следовать путём Мага или этот путь для тебя завершён?

— Завершен. Тем не менее, я благословляю мой магический опыт. Проживание этого опыта искренне побудило меня вернуться к первоистоку, к целостности. Мне предлагают снять с себя магические артефакты и встать в центр Часов.

— Что необходимо сделать, чтобы активировать Божественные Часы?

— Появился опять Саи Баба и предлагает выразить намерение о соединении Серебряной Струны с Часами. Ещё он говорит, что у тебя есть какой-то числовой ряд. Он — ключ к активации. Перед внутренним взором возникает образ Человека Леонарда да Винчи.

— Я понял. Сколько раз читать?

— Прошу богоцентрировать весь процесс и направляю действие энергии числового ряда на активацию Божественных Часов.

Читаю вслух 12 раз

1 1 2 3 5 8 4 3 7 1 8 9 8 8 7 6 4 1 5 6 2 8 1 9…

В процессе чтения стрелки на Часах пошли.

По серебряной струне пошла энергия, которая соединила все уровни Юриной Монады, а также — земную и небесную энергии…

Самое неожиданное в этом процессе было то, что на Часах появились четыре Сущности, которые являются некоторыми частями Единого Целого с Юрой.

Во время общения выяснилось, что когда-то произошло разделение Центральной Души, и каждая часть выбрала свою область в мироздании для реализации.

Было принято решение об интеграции, что и произошло в центре Божественных Часов.

Результатом этого процесса явилось создание на этом уровне Общего Кристалла.

После этого, я вспомнил, что Саи Баба как-то говорил о неком Плане, который предполагает соединение сначала двух Сущностей в одно, потом четырёх и так далее по бинарному принципу.

Безусловно, что этот числовой ряд не является панацеей. Это всего лишь инструмент, позволяющий быстро произвести необходимую работу с человеком, сонастроить его вертикально с разными уровнями Бытия.

Источник

Здравствуйте! Возник такой вопрос: необходим найти матрицу A, которая удовлетворяла бы следующему условию:

Матрица из двух строк X(n) и X(n+1)=A^n*матрица из двух строк x(0) x(1), где x0 и x1 равны 1.

Как бы А легко ищется подбором, но не могу понять как доказать это для всех n, предполагаю, что необходим метод мат индукции.

задан 5 Сен ’17 19:49

@driver: из описания не очень ясно, какому свойству должна удовлетворять матрица. Что касается матриц из чисел Фибоначчи, то известно, что если взять матрицу A=( 1 1 // 1 0 ), то её степени будут иметь вид A^n= (f_n f_ // f_ f_ ), где f_<-1>=0, f_0=1, и далее f_k=f_+f_ при всех k>=1. Доказывается это индукцией по n, причём очень легко. Домножаем A^n на A слева или справа, и смотрим, что получится. Отсюда видим, что A^ устроена по этому же закону.

@falcao спасибо за ответ, необходимо найти матрицу А, подставив которую, не нарушится равенство: Матрица из двух строк X(n) и X(n+1)=A^n*матрица из двух строк x(0) x(1), где x0 и x1 равны 1. Опять же, саму матрицу я нашел, как доказать, что при этой матрице равенство при любых n будет соблюдаться? У меня с мат индукцией плохо, подскажите, пожалуйста.

@falcao да, она 2 на 2; X(n)=X(n-1)+X(n-2), n>=2; да, то же самое.

@driver: осталось понять, как заданы начальные значения, то есть строки x(0) и x(1). Проще всего будет их записать в виде двумерных векторов типа ( 7 3 ) и т.п.

@falcao я же ранее писал, что они оба равны 1

@driver: именно это меня и смутило, почему я и попросил уточнить. Говорится о векторах, а равны они почему-то числам. Может быть, имелось в виду, что x(0)=x(1)=( 1 1 )? Но тогда зачем две одинаковые координаты? Ведь тогда для всех n оно так и останется.

@driver: правильно ли тогда, что под матрицей из двух строк X(n) и X(n+1) понимается вектор-столбец из двух этих чисел Фибоначчи? Если да, то всё должно быть достаточно просто.

1 ответ

Будем для краткости изображать вектор-столбец из двух чисел в виде (u v)^T.

В условии рассматривается последовательность чисел Фибоначчи: x(0)=x(1)=1; x(n)=x(n-1)+x(n-2), n>=2. Требуется найти матрицу A размеров 2×2, для которой (x(n) x(n+1))^T=A^n(1 1)^T. Для n=0 это всегда верно.

отвечен 5 Сен ’17 21:29

@falcao это я сделал, но как доказать это для других n?

@driver: то условие, которое здесь было рассмотрено, означает, что проходит шаг индукции. Если то равенство, которое дано в условии, верно для какого-то n=k, то после домножения на A получится равенство для n=k+1. Это как бы самоочевидные вещи.

Здравствуйте

Источник

Происхождение и применение последовательности Фибоначчи

От Фибоначчи до Эллиотта

Автор: Джеффри Кеннеди

Вы скажете, что это ещё одно модное или «умное» словечко, которое чаще используют, чтобы произвести впечатление, чем чтобы объяснить. Несколько лет назад модным словечком, которое я слышал чаще всего, было «беспроигрышный» — концепция, популяризированная Стивеном Кови. К сожалению, в последние годы технические аналитики подняли «Фибоначчи» на тот же уровень. Понимание этого термина, возможно не спасёт его от статуса «умного слова», но даст некоторое представление о причинах его популярности.

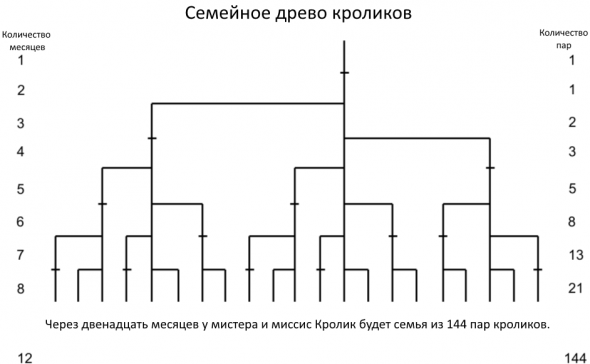
Леонардо Пизанский Фибоначчи был математиком в тринадцатом веке, который задал вопрос: сколько пар кроликов может появиться от одной пары в закрытой среде за год, если каждая крольчиха рождает пару крольчат каждый месяц, а способность к производству потомства у них появляется по достижению двухмесячного возраста? Ответ: 144.

Гениальность этого простого маленького вопроса не в ответе, а в последовательности чисел, с помощью которой был найден ответ: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 и 144. Эта последовательность чисел представляет собой увеличение популяции кроликов в течение 12-месячного периода и называется последовательностью Фибоначчи.

Поскольку Леонардо Фибоначчи изначально изучал размножение наших маленьких пушистых друзей, актуальность этого соотношения была доказана снова и снова. Во всём, от цепочки ДНК до галактики в которой мы живём присутствуют уровни Фибоначчи, они определяют естественный прогресс роста и распада. Простым примером является человеческая рука, состоящая из пяти пальцев, каждый из которых состоит из трёх костей.

Помимо открытия того, что фондовый рынок состоит из волн, образующих повторяющиеся паттерны, Р. Н. Эллиотт также осознал важность уровней Фибоначчи. В последней книге «Закон природы» он особенно подчёркивал последовательность Фибоначчи как математическую основу Волнового Принципа. Благодаря его открытиям мы используем уровни Фибоначчи при вычислении коррекции волн и проекций.

Мы также переводим непубличные статьи из MyEWI, где публикуется более детальная информация. Подписывайтесь>>>

Источник