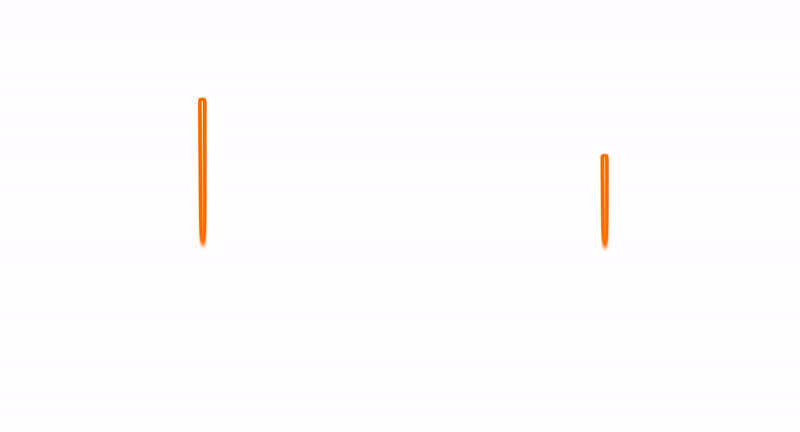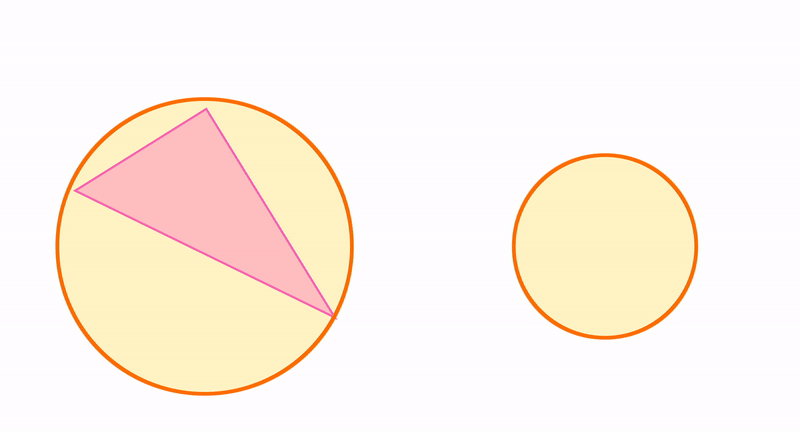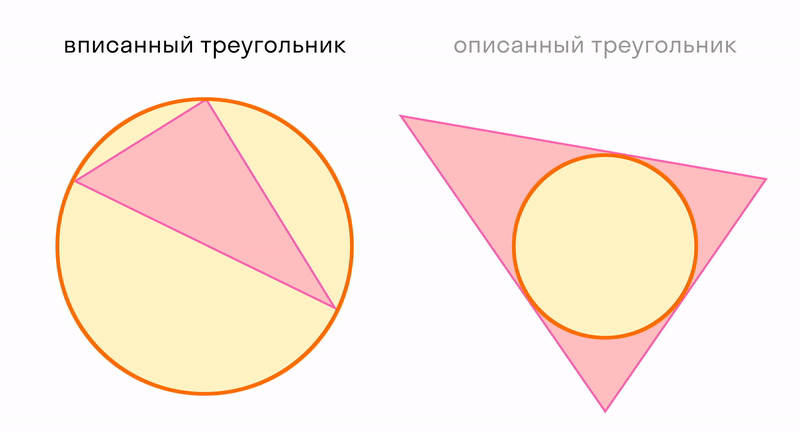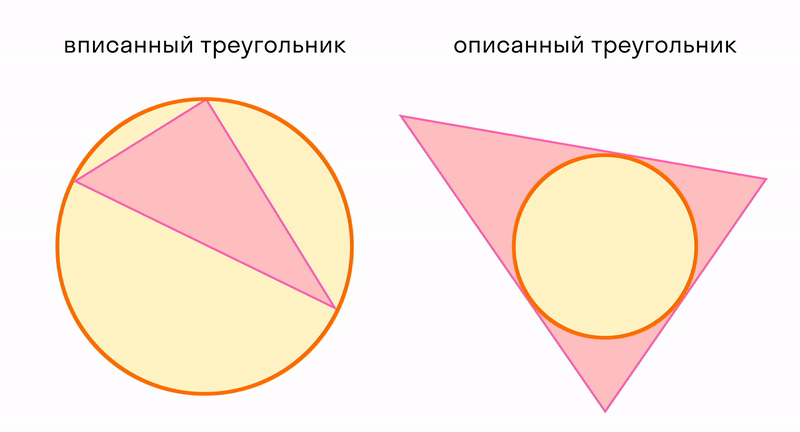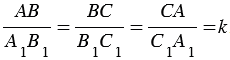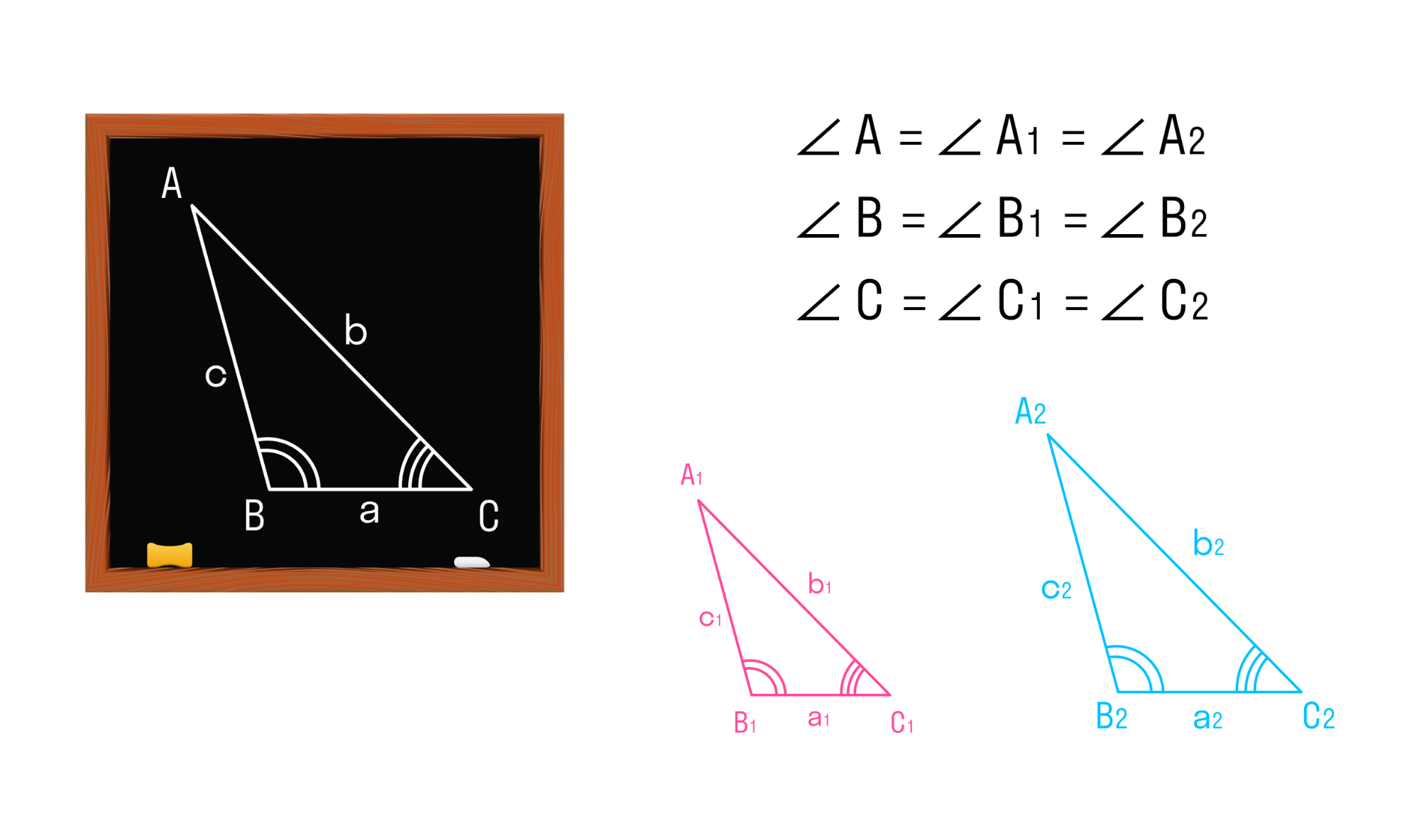С чего начинаются азы геометрии
Геометрия с нуля
Разделы: Математика
В 21 веке, несмотря на активное развитие науки, у многих школьников Российской Федерации такая наука, как геометрия вызывает все больше затруднений, а какая-то часть детей и вовсе не может решать простейшие геометрические задачи. Поэтому необходимо признать тот факт, что восприятие у нового поколения совершенно иное, и дело тут вовсе не в их деградации. Дети все также хотят развиваться: читают книги, смотрят научные фильмы и проводят эксперименты. Но самое главное, чего они не хотят, так это заучивать то, чего не понимают. На основе этого утверждения как раз и будет построена моя программа.
Представим, что перед нами сидит человек, который вообще не представляет, что такое геометрия. А именно так и выглядит бОльшая часть детей приходящих в 7 класс. Этот человек не в состоянии накладывать треугольники друг на друга и тем более не может делать из этого какие-то выводы. Поэтому сначала его нужно долго и упорно знакомить его с геометрией, чтобы в итоге он понял, насколько она проста и полюбил ее.
Разделение на уровни
Именно эти три пункта будут подробно описаны в статье.
Базовый уровень (простейшая теория и задачи)
— понятие точки, прямой, луча, отрезка, угла, фигуры и т.д.
Прежде всего, школьник должен понять, с чем он будет иметь дело на протяжении ближайших трех лет, поэтому начинать необходимо с вводного курса. Не надо давать детям сложные задачи, а их надо просто познакомить с геометрией.
Углам нужно уделить особое внимание, потому что далеко не все дети могут в пространстве могут отличить тупой угол от прямого. Кроме того, максимум внимания нужно уделить развернутому углу, потому что на нем будет основан следующий пункт.
Многим детям тяжело запомнить существующее определение смежных углов, и именно в большинстве случаев начинаются первые проблемы с геометрией. Поэтому мною будет предложено новое определение смежных углов: “Смежные углы – это углы, полученные в результате деления развернутого угла на две части.” Если уделить должное время развернутому углу, то получится сэкономить время на объяснении свойства смежных углов, т.к. оно итак будет понятно.
Вертикальные углы, также как и смежные, имеют весьма непростое определение, которое можно заменить ан более просто. Достаточно ограничиться следующим: “Вертикальные углы-это углы между пересекающимися прямыми.”, а далее просто постараться разобрать как можно больше примеров, связанных с вертикальными и смежными углами.
Этой теме я не стану уделять много внимания, т.к. он итак понятен большинству школьников.
Вместо равенства треугольников гораздо лучше рассматривать параллельные прямые, т.к., помимо получения новой информации, дети закрепляют старую, используя вертикальные и смежные углы при решении задач на параллельные прямые. Объяснять данную тему проще с признака, основанного на внутренних односторонних углах, т.к. единственное, что запоминают дети после шестого класса, это что сумма углов треугольника равна 180 градусам. Опираясь на это можно представить, что прямые пересекутся и образуют с секущей треугольник, сумма углов которого равна 180 градусам. А после этого показать детям вариант, при котором треугольника не будет, т.е. когда внутренние односторонние углы заберут градусную меру третьего угла треугольника. После этого остальные признаки доказать уже будет не так и сложно. Самое главное, не надо заставлять детей учить первые доказательства, т.к. они должны их понять.
— биссектриса, высота и медиана
После всех предыдущих тем, ребенок будет понимать, что такое углы и уметь с ними работать, а также будет знаком с прямыми, отрезками, фигурами и прочим. В этот момент ему уже можно давать более-менее сложные темы, которые ему в дальнейшем будут постоянно пригождаться. В определениях ничего менять не стоит, т.к. они итак максимально доступны. Единственное, что нужно обязательно сделать, так это убедиться в том, что ребенок может провести биссектрисы, медианы и высоты в любой фигуре и из любой вершины!
— треугольники *(при объяснении свойств треугольников можно и нужно опираться на признаки равенства)
Теперь, когда школьник со знаком с основами, можно приступать к рассмотрению фигур. Начать лучше всего с треугольников, т.к. именно они используются в большинстве задач. Здесь необходимо рассмотреть все виды треугольников с их свойствами. Объяснить ребенку откуда что берется, опять же не заставляя это заучивать. Но определения и свойства школьник должен знать, т.к. именно на этапе прохождения свойств фигур, мы можем начинать спрашивать с ребенка теорию. Теперь он уже полноценно вовлечен в процесс.
— четырехугольники *(при объяснении свойств четырехугольников можно и нужно опираться на признаки равенства)
Здесь я бы хотела представить Вашему вниманию увлекательный процесс эволюции параллелограмма, который детям запомнить гораздо проще, чем определения из учебника:
Здесь рассмотрены только те свойства, которые способен легко усвоить школьник на базовом уровне.
Кроме того, сюда же необходимо включить и трапецию со всеми ее свойствами и разновидностями.
Таким образом, мы сможем закрепить параллельные прямые и понять, откуда что берется в четырехугольниках.
В этой теме необходимо рассмотреть разные виды многоугольников и сумму углов n-угольника.
Тема, которую итак все прекрасно понимают, поэтому ничего усложнять не надо.
Здесь я опять же хочу предложить удобную схему, которую необходимо объяснять с помощью бумажных фигурок.
Трапеция опять же рассматривается отдельно.
— подобие и первый признак подобия
Рассматривается исключительно в ознакомительных целях, чтобы детям легче было понимать начала тригонометрии.
— средние линии треугольника и трапеции
Средние линии лучше рассматривать вместе, потому что так они лучше усваиваются.
В самом начала тригонометрии, школьникам стоит напомнить о том, что такое соотношения, а после очень много времени посвятить самим определениям синуса, косинуса, тангенса и котангенса, чтобы школьники понимали, откуда взялись эти странные английские буквы. Затем необходимо рассмотреть множество задач, в которых они будут использоваться. Удобнее всего давать задачи на теорему Пифагора и площади. Желательно уже на базовом уровне ознакомить детей с таблицей, т.к. сейчас они уже максимально близки к среднему и уровню и способны усваивать информацию средней сложности.
И, наконец, последняя тема на базовом уровне. Здесь необходимо напоминать детям обо всем, что связано с окружностью и кругом, начиная с определений, т.к. никто уже ничего не помнит из курса 6 класса. А также стоит рассмотреть свойство касательной, вписанный и центральный углы, и свойство гипотенузы прямоугольного треугольника.
На этом базовый курс окончен. У рядового школьника достаточно базовых знаний, на которые он мог бы опираться при решении задач, с использованием доказательств. Пришла пора поближе с ними познакомиться.
Средний уровень (доказательства)
Расписывать программу для среднего уровня смысла нет, т.к. на этом этапе ребенок готов усваивать практически любую информацию и способен аргументированно решать задачи на доказательства. Единственное, что стоит сделать, так это перечислить темы среднего уровня:
— соотношения между сторонами и углами;
— признаки равенства треугольников;
— признаки подобия треугольников;
— четыре замечательные точки;
— вписанная и описанная окружности.
Этого вполне достаточно для доказательств средней степени сложности.
Высокий уровень (сложные доказательства и решение сложных задач)
К сожалению, немногие могут достичь высокого уровня, но каждый должен хотя бы попытаться. Опять же, нет смысла все подробно расписывать, поэтому будут перечислены лишь темы:
— углы при окружности;
Из всего вышесказанного можно сделать следующий вывод: прогресс любого школьника основан на его базовых знаниях. Если они есть, то их необходимо лишь грамотно развивать. Поэтому, прежде всего, необходимо упростить получение базовых знаний и сделать их максимально доступными для всех школьников без исключения.
Примечание: векторы в статье не учтены, т.к. являются дополнением ко всему вышесказанному.
С чего начинаются азы геометрии
Геометрия — математическая наука о пространственных формах, размерах и соотношениях геометрических объектов (фигур, тел). Слово «гeoметрия» греческого происхождения («geo» — земля, «metreo» — измеряю).
Планиметрия — раздел геометрии,в котором изучают свойства фигур,расположенных в одной плоскости. Слово «планиметрия» происходит от латинского корня «planum» — плоская поверхность и греческого — «metreo» — измеряю.
Стереометрия — раздел геометрии, в котором изучают свойства пространственных тел. Слово «стереометрия» происходит от греческих слов «stereos» — пространственный, «metreo» — измеряю.
Периоды развития геометрии
I период — зарождение геометрии как математической науки, начало которого теряется в глубине столетий, а концом считают V в. до н.э. Этот период характеризуется накоплением фактов и установлением первых зависимостей между геометрическими фигурами. Начался он в Древнем Египте и Вавилоне, в VII в. до н.э. Эти знания были перенесены в Грецию, где постепенно они начали оформляться в четкую систему.
II период — (V в. до н.э. — XVII в. н.э.) — период возникновения и дальнейшего развития геометрии как самостоятельной науки. Около 300 лет до н.э. появились «Начала» Эвклида, в которых гeoметрия была систематизирована. Развитию геометрии способствовали ученые Греции, арабского Востока, Средней Азии, Индии, Китая, средневековой Европы.
III период — (XVII в. — 1826 г.). На этом этапе геометрия как наука рассматривает более общие фигуры и применяет совершенно новые методы. В этот период возникают: аналитическая геoметрия, дифференциальная геомeтрия, проективная геoметрия, начертательная гeометрия.
IV период — (1826 год) начинается с открытия Н. И. Лобачевским неэвклидовой геометрии, которая включает в себя геометрию Эвклида. В направлениях, начертанных выдающимися математиками, развивается современная геомeтрия. Одним из важных разделов современной геометрии является топология.
Источники идей и цитат для конспектов по Геометрии:
(с) Цитаты из вышеуказанных учебных пособий использованы на сайте в незначительных объемах, исключительно в учебных и информационных целях (пп. 1 п. 1 ст. 1274 ГК РФ).
Основы геометрии
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Идеальные объекты
Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.
Основные геометрические объекты: окружность, квадрат, ромб, прямоугольник, равносторонний треугольник, равнобедренный треугольник, правильный многоугольник, эллипс и другие.
Все эти фигуры обладают двумя свойствами:
Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.
У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.
Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).
Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.
Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.
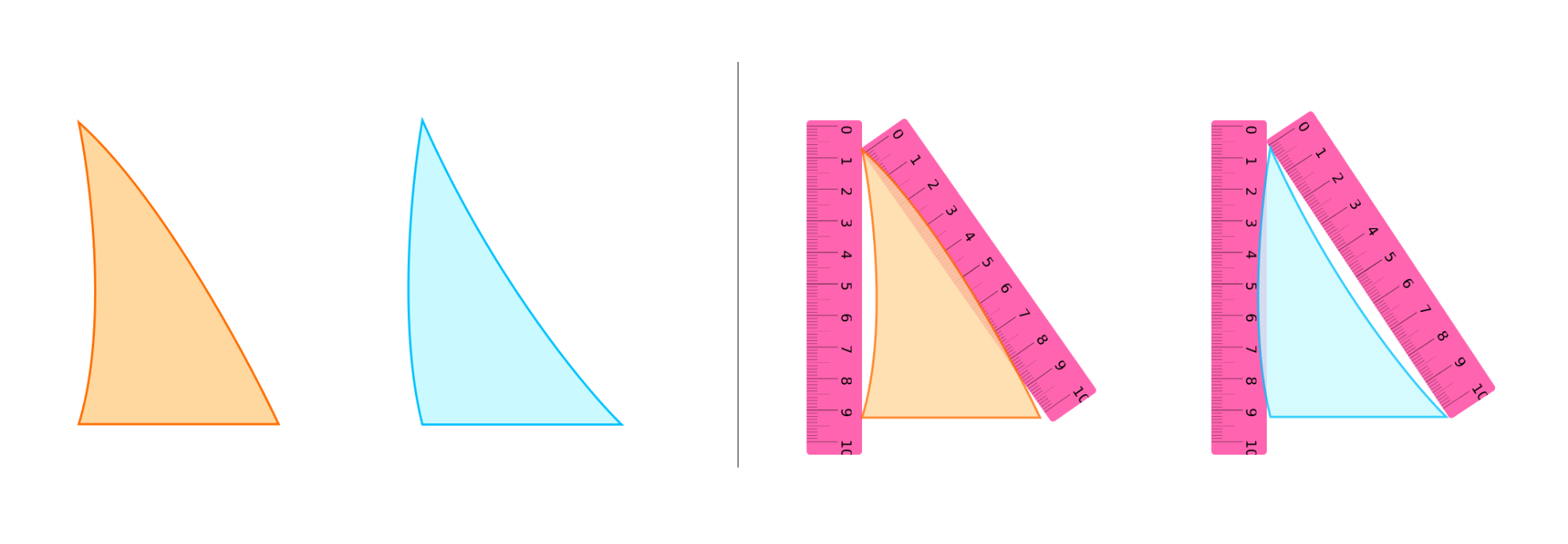
Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.
Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.
Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Базовые геометрические объекты
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.
Точка — это идеальный математический объект, у которого нет длины и ширины.
Отрезок — это часть прямой, у которого есть начало и конец.
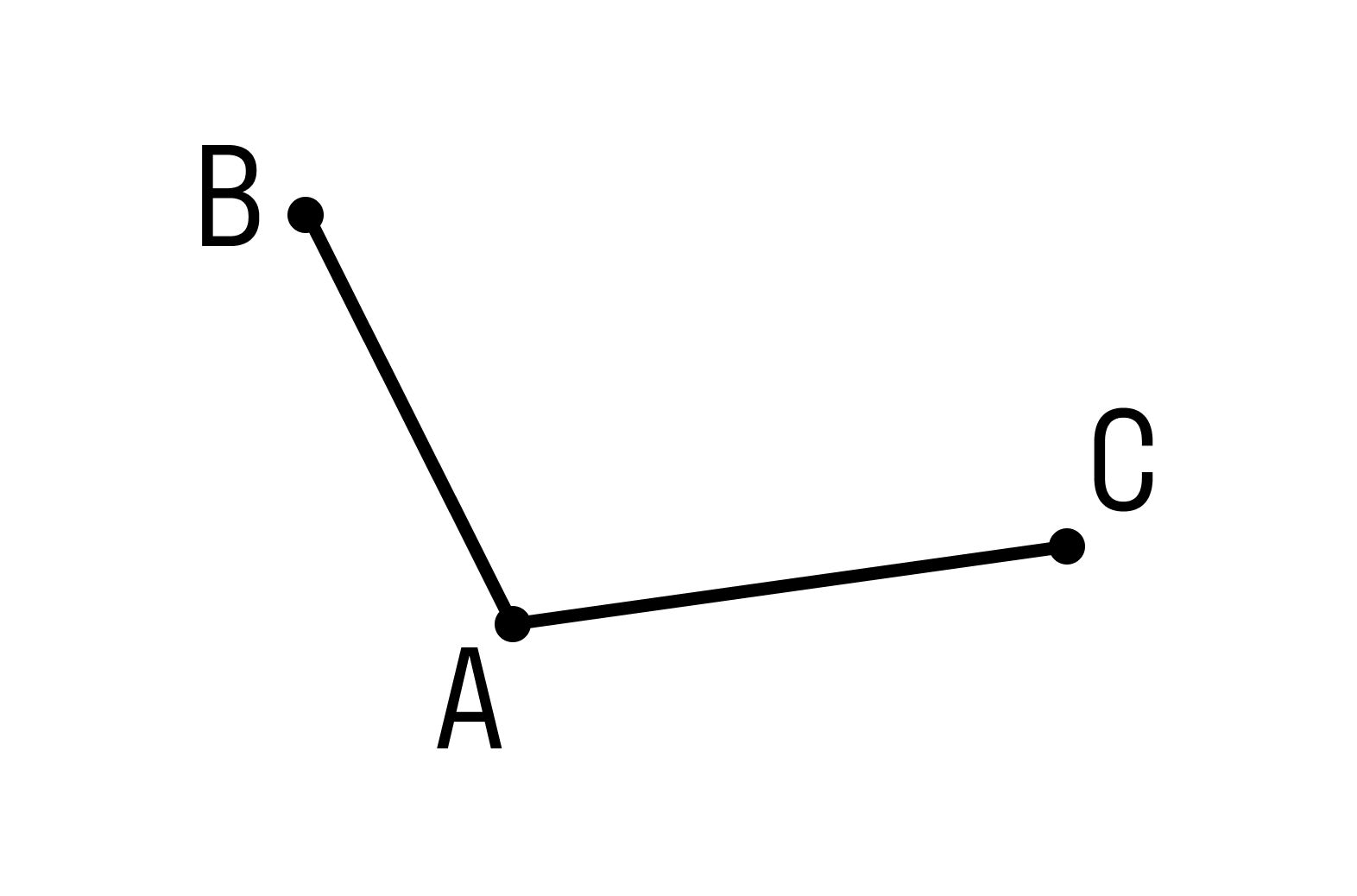
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.
Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.
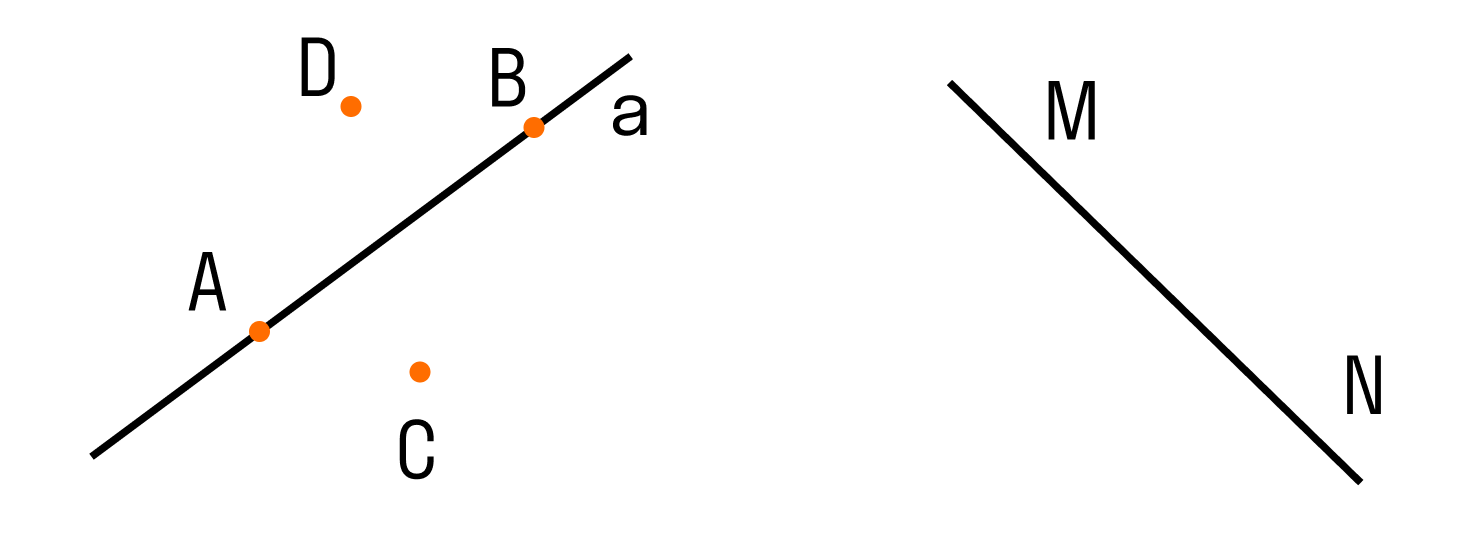
Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).
Два варианта расположения точек относительно прямой:
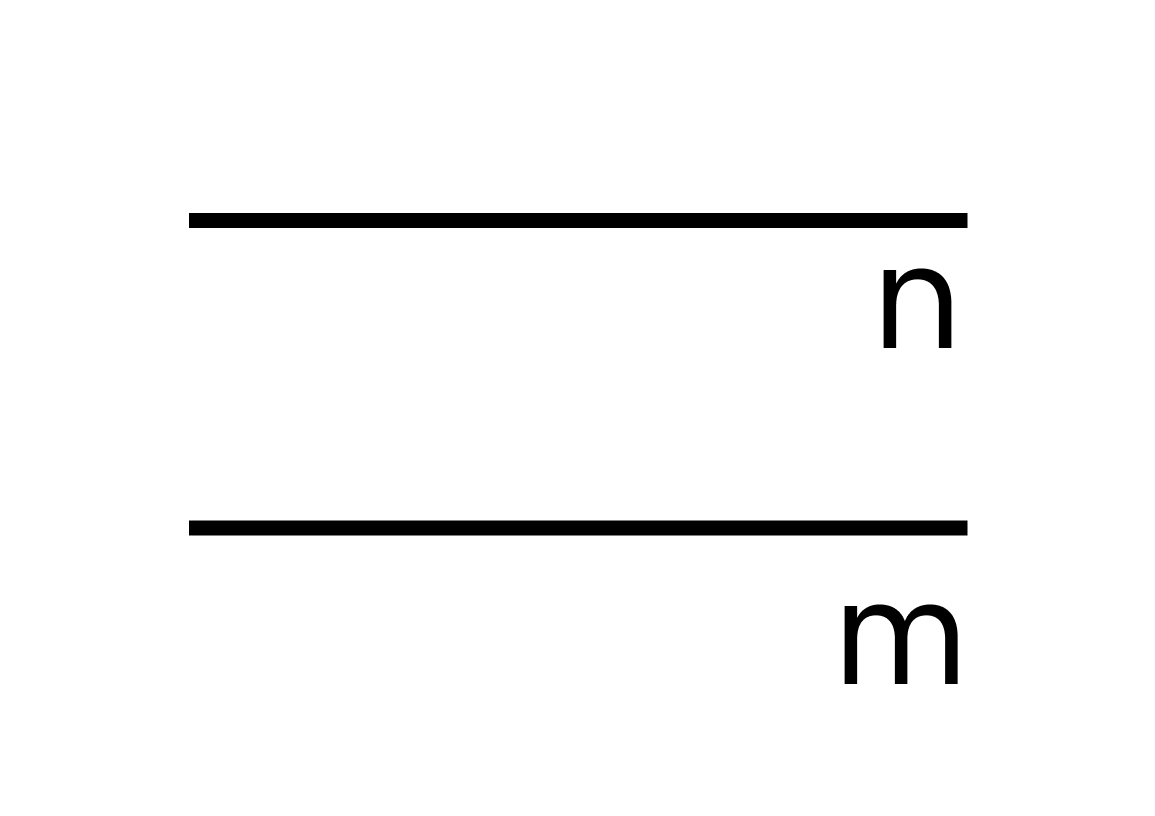
Если рассмотреть две прямые, то возможны два варианта их расположения:
Для записи не пересекающихся прямых используют специальный знак — 
то есть m 
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
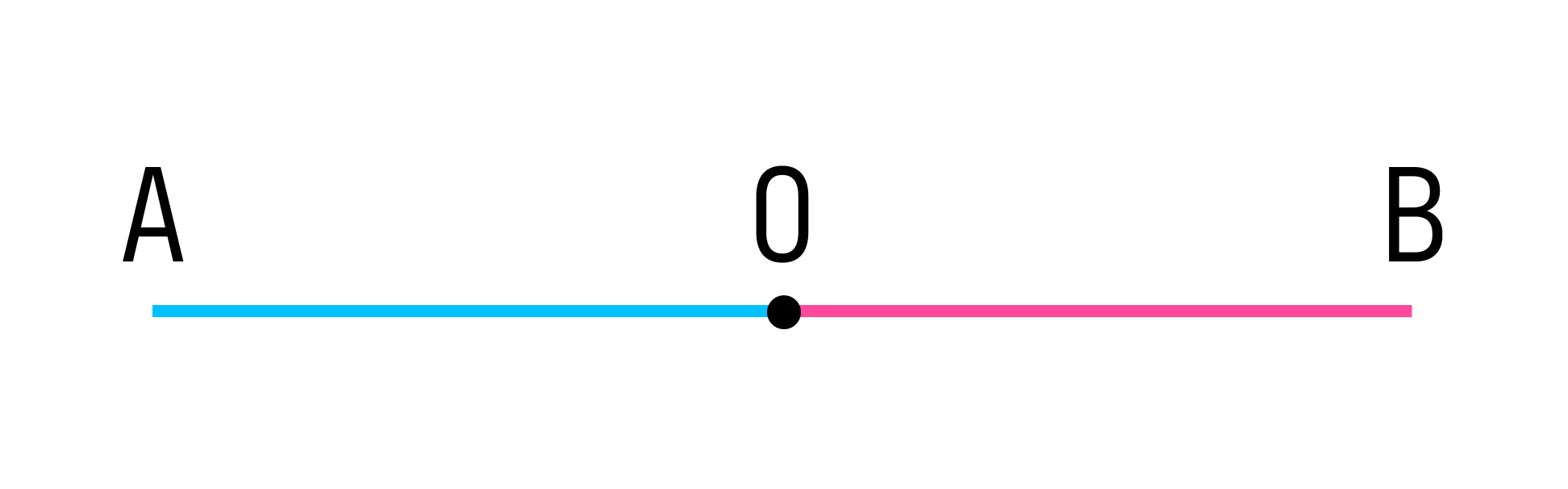
На рисунке точка О разбивает прямую АВ на две части:
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.
Назовем получившиеся лучи:
Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.
Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости
Комбинации простейших объектов
Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
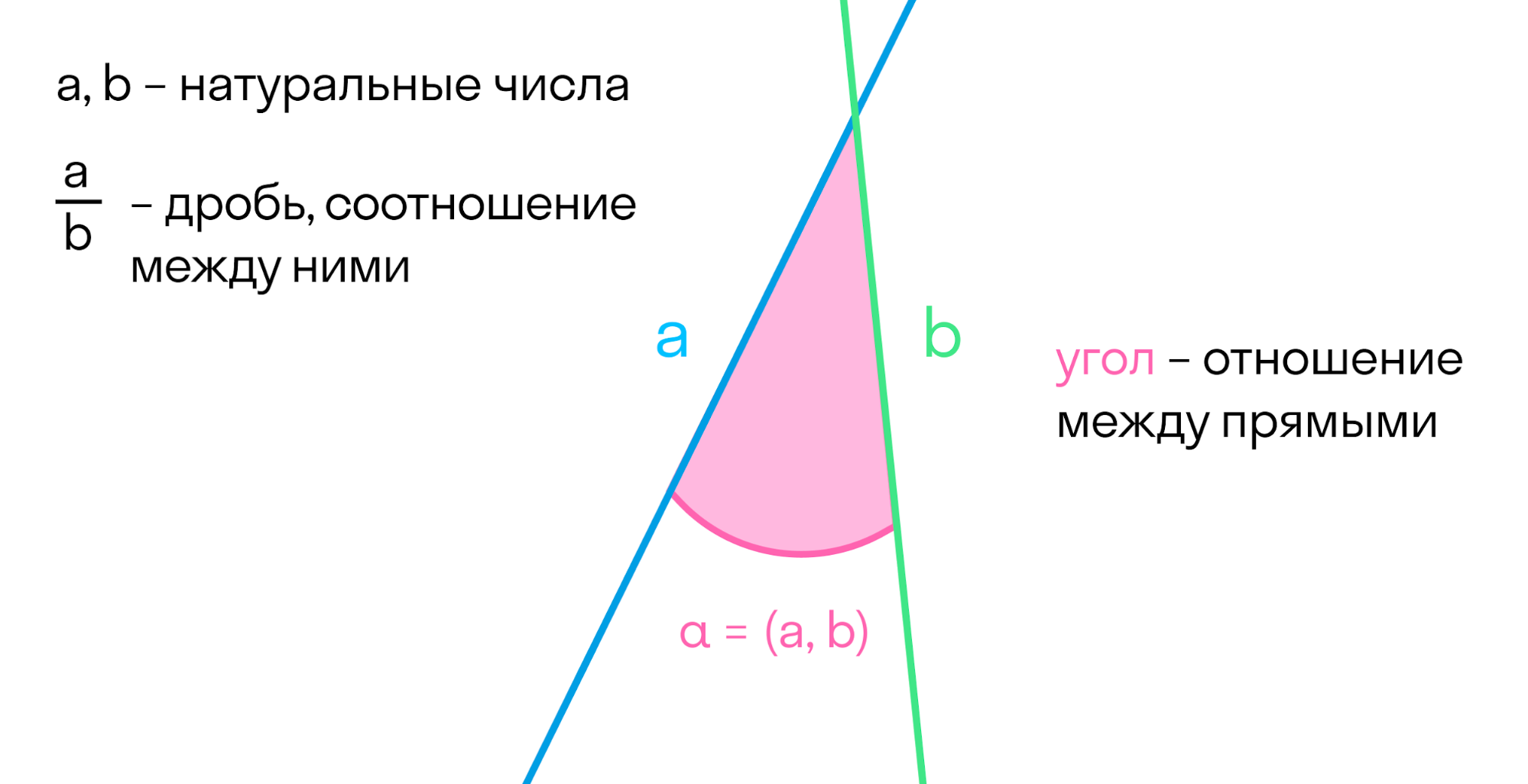
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.
Точно так же мы изучали множества, а после — отношения между множествами, функции.
Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
Максимальный угол – это полный оборот, он составляет 360 градусов.
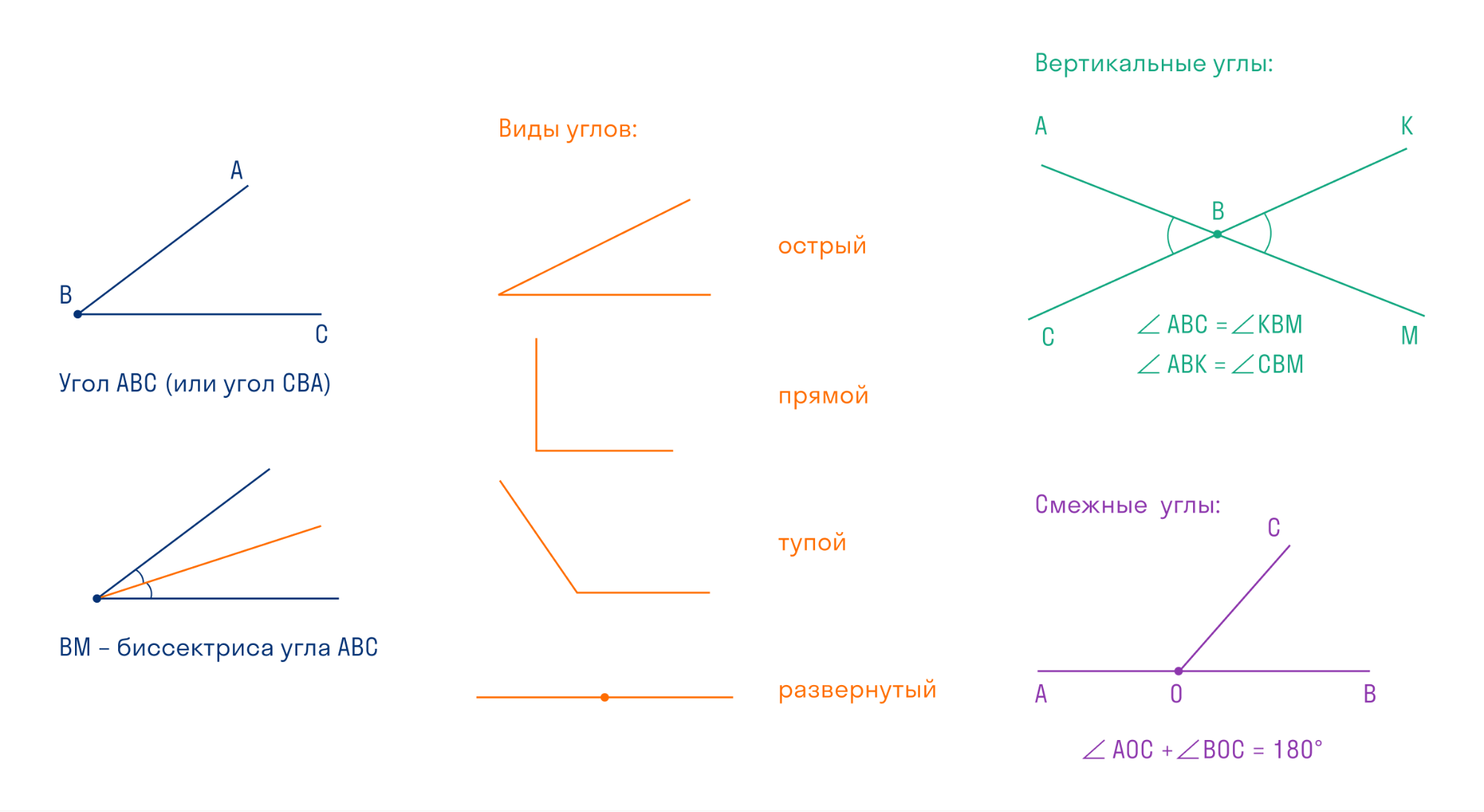
Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
Есть разные виды углов, выделим самые часто встречающиеся:
Точка называется вершиной угла, а лучи — сторонами угла.
Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.
Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.
А теперь посмотрим на взаимное расположение трех прямых.
Первый случай: все три прямые параллельны.
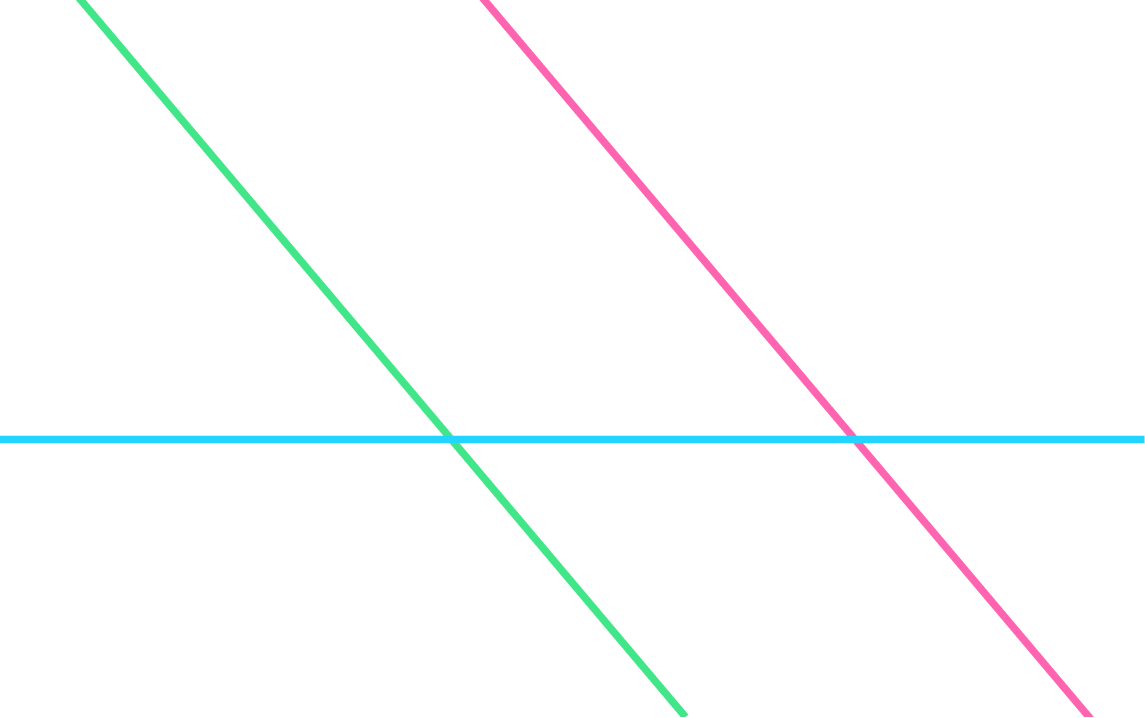
Второй случай: две прямые параллельны, а третья их пересекает.
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.
Треугольник
Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
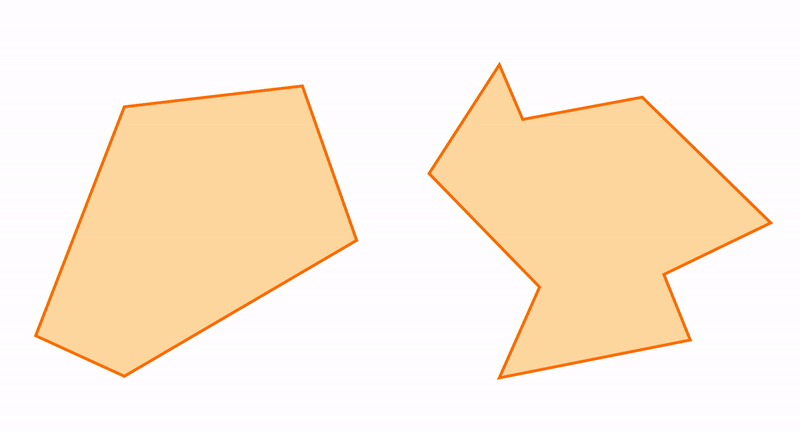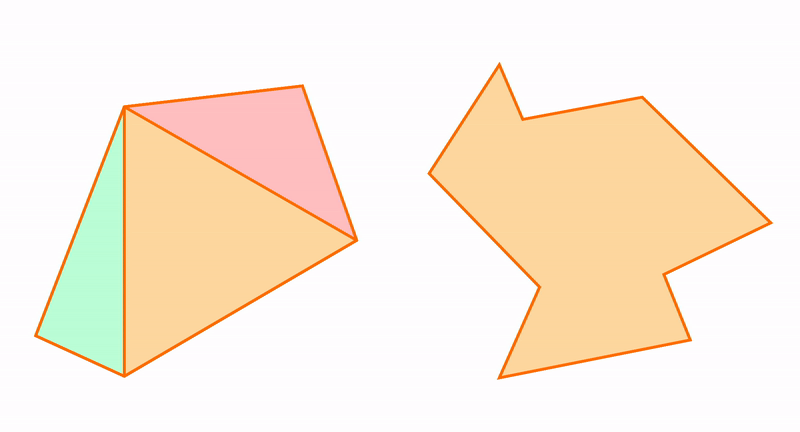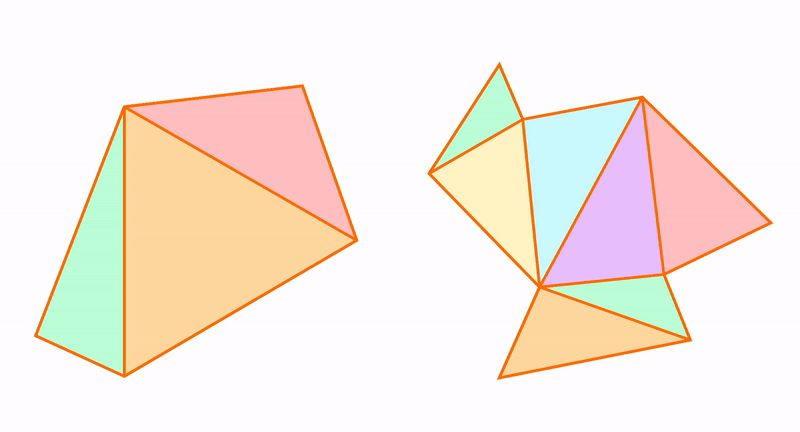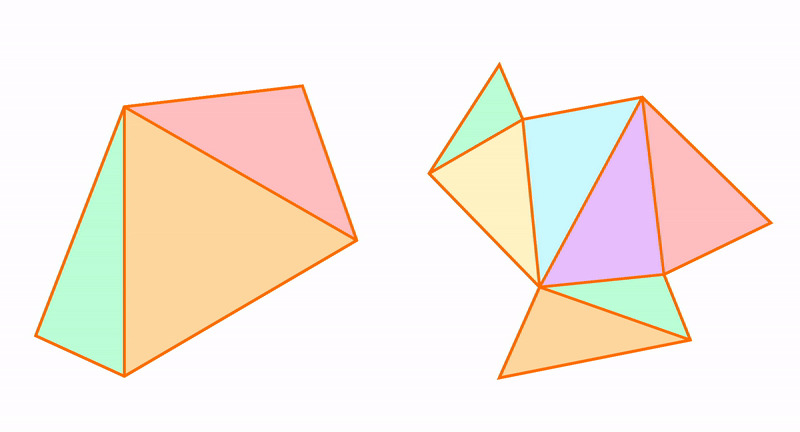
Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.
Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.
Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:
Приходи на наши онлайн уроки по математике с лучшими препадавателями! Для учеников с 1 по 11 классы!
Свойства треугольников
Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.
Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.
Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.
Сумма любых двух сторон треугольника больше его третьей стороны.
Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.
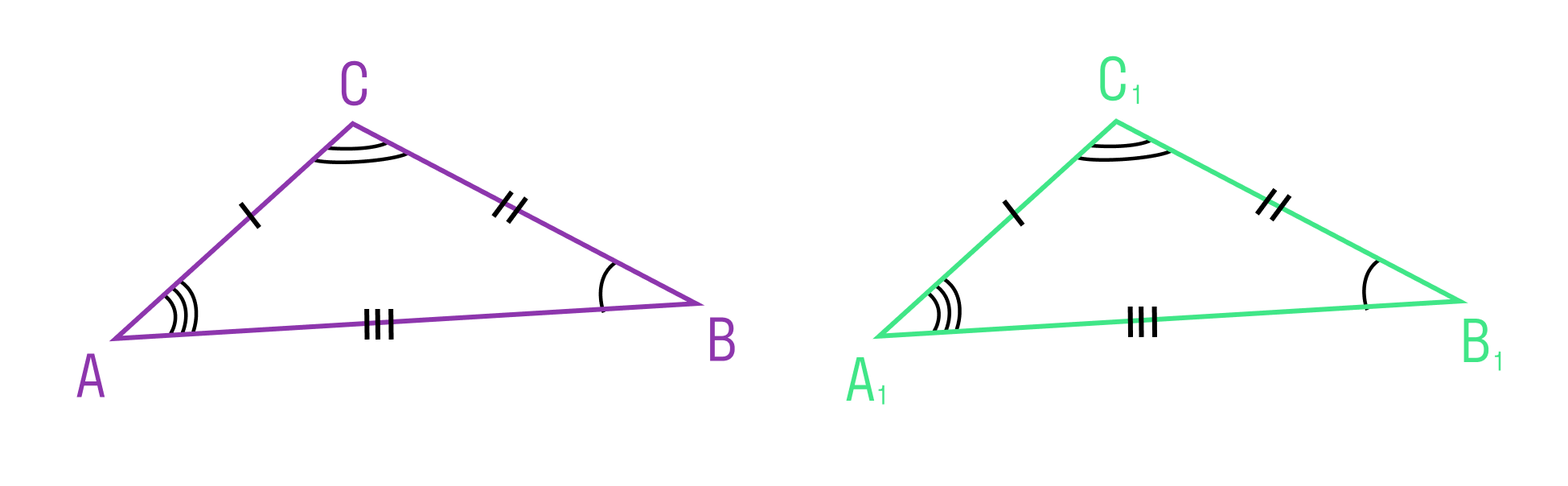
Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.
Равенство треугольников ABC и A1B1C1 обозначается так: ΔABC = ΔA1B1C1.
Есть даже специальные теоремы про равенство треугольников.
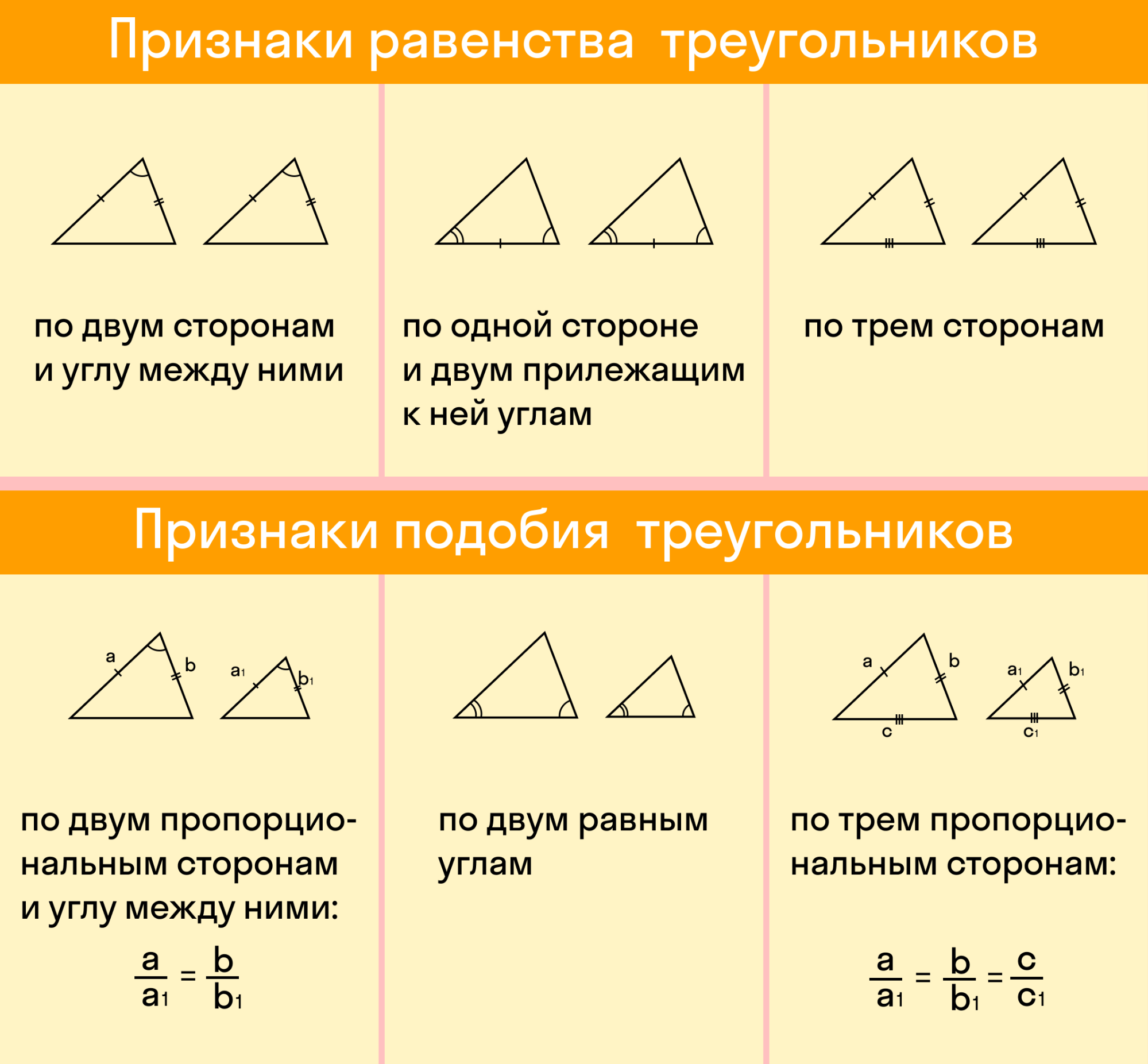
Первый признак равенства треугольников звучит так:
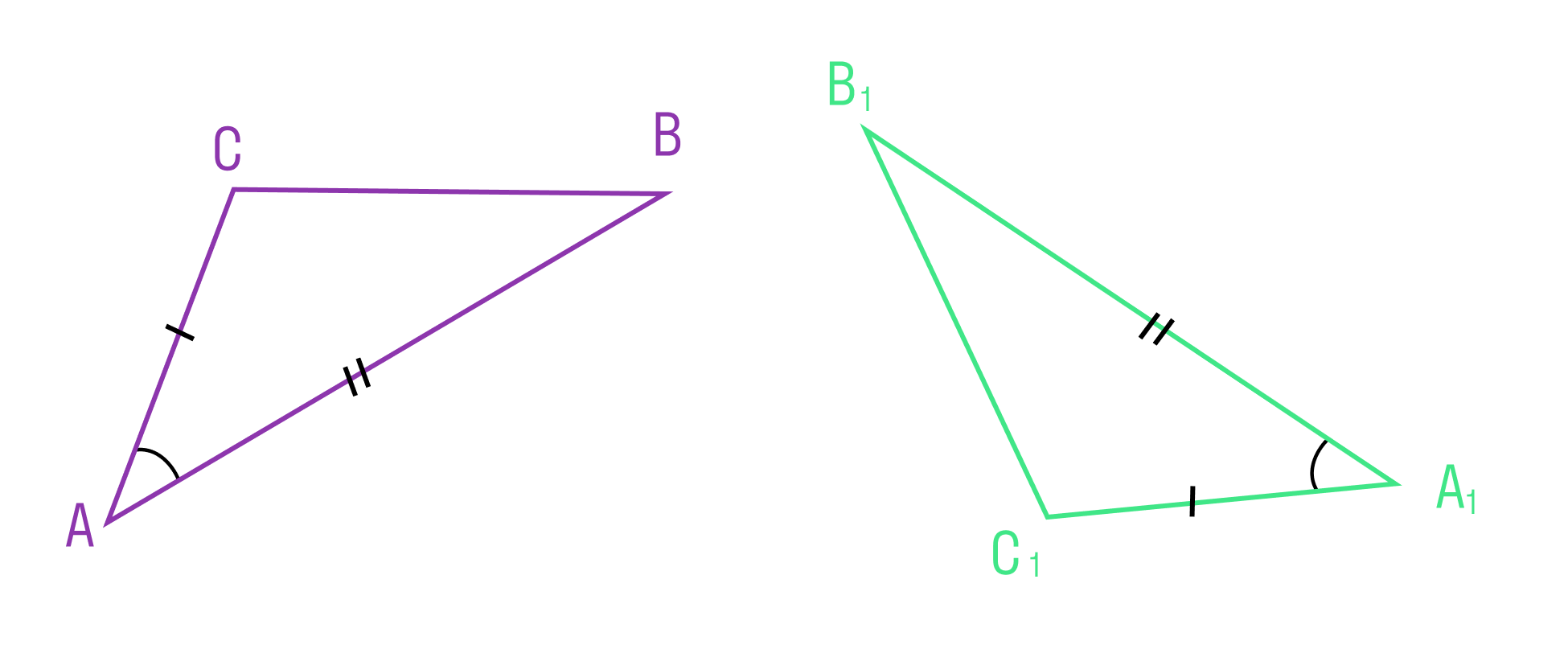
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
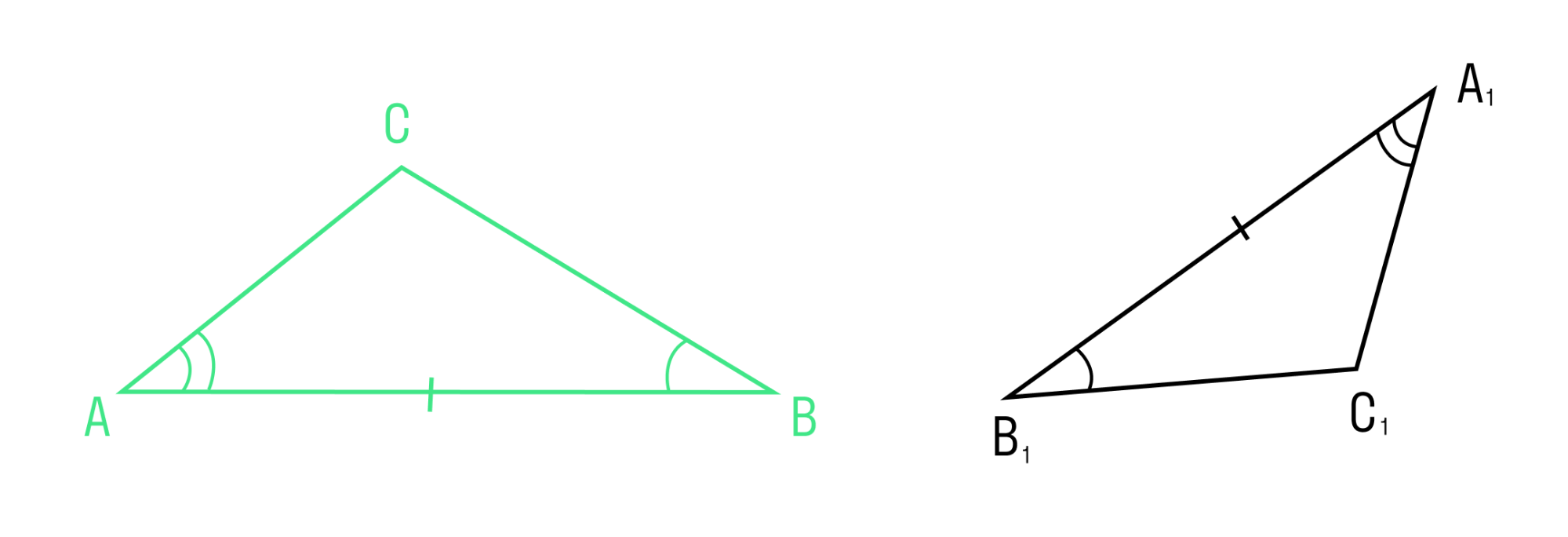
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
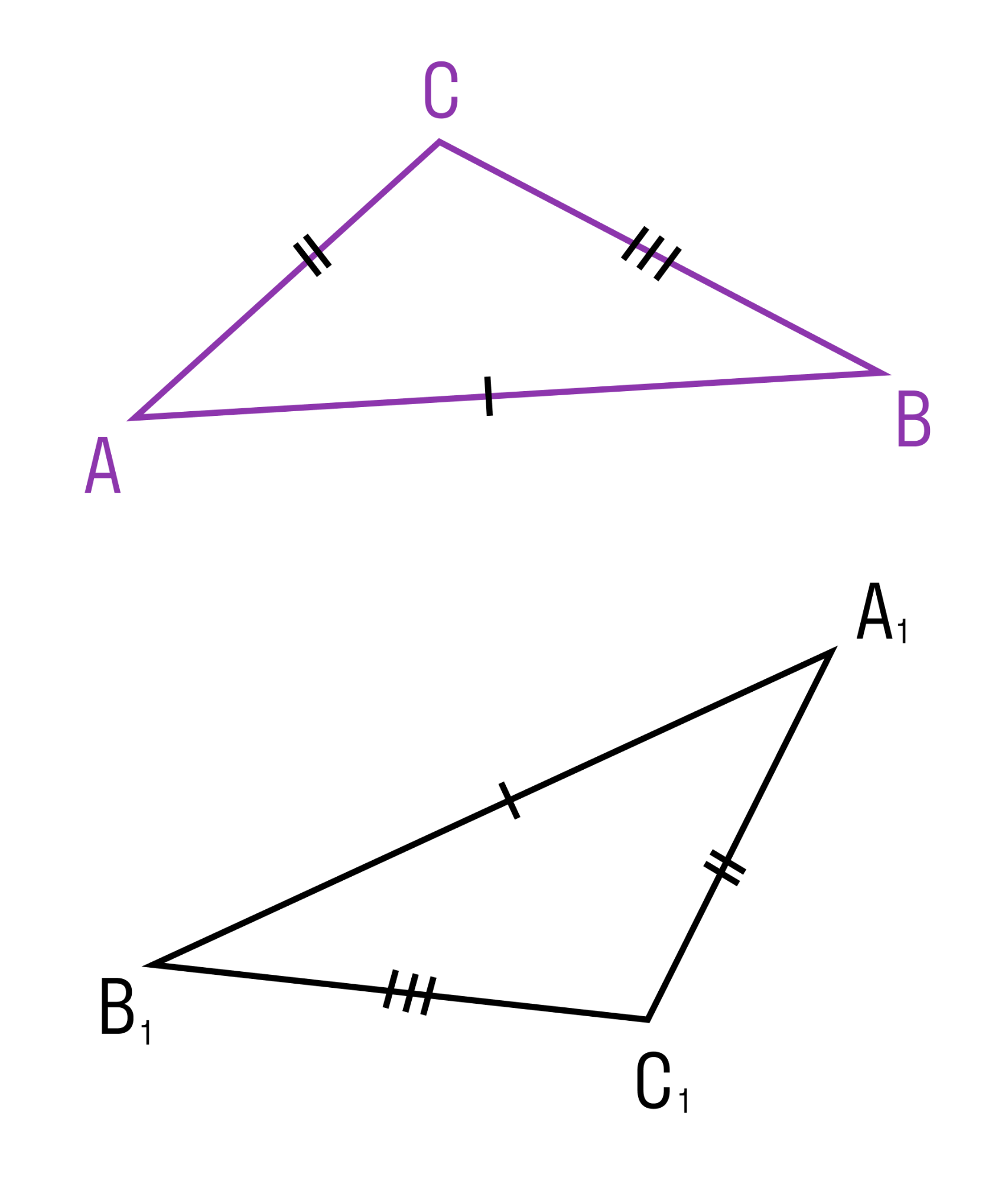
Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.
Подобные треугольники
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Треугольники АВС и A1B1C1 будут подобны, если
Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Подобие треугольников обозначают специальным символом — ∾. На рисунке треугольники АВС и A1B1C1 подобны, это можно записать так: ΔАВС ∾ ΔA1B1C1.
Теорема о первом признаке подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
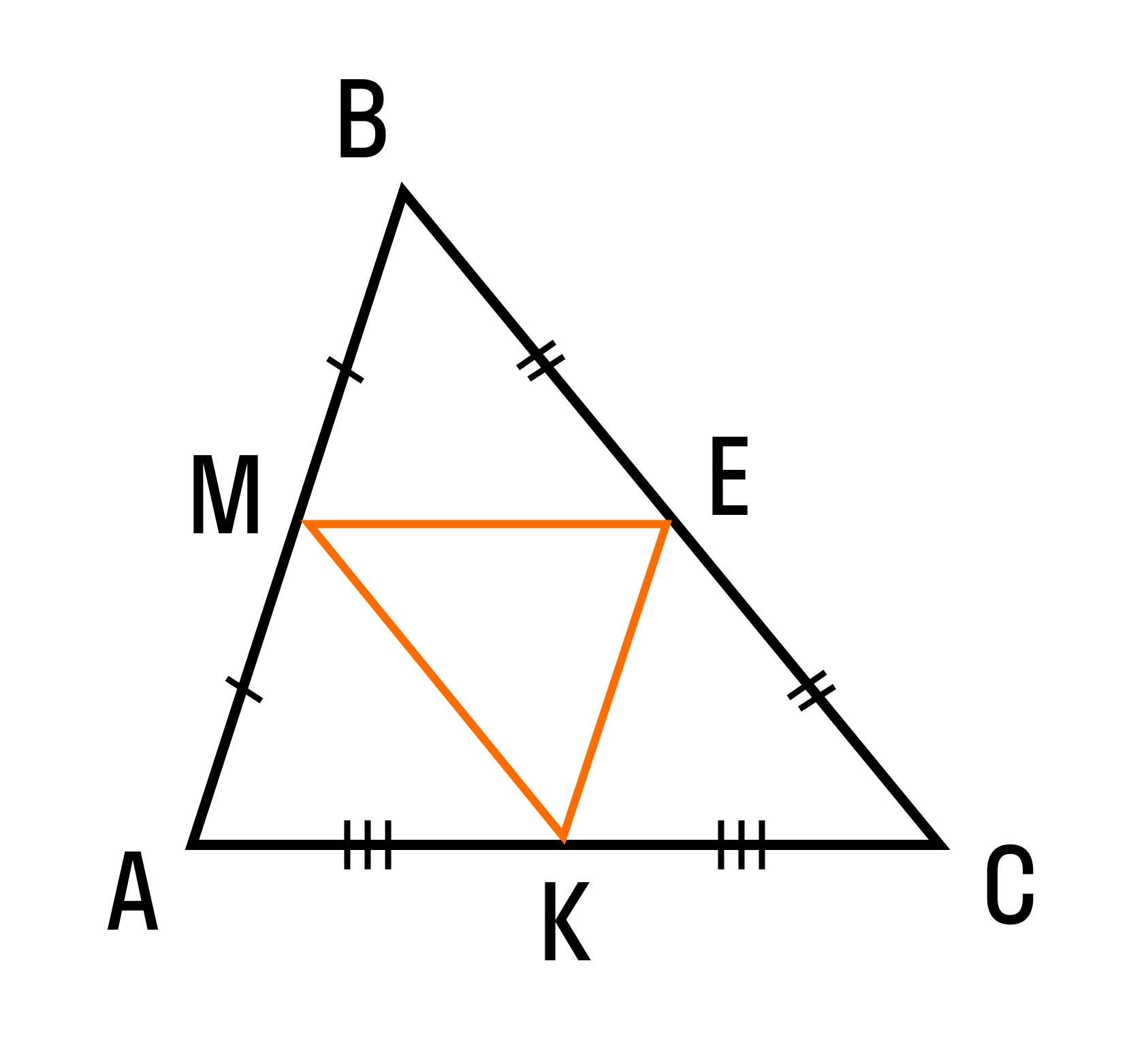
Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.
На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
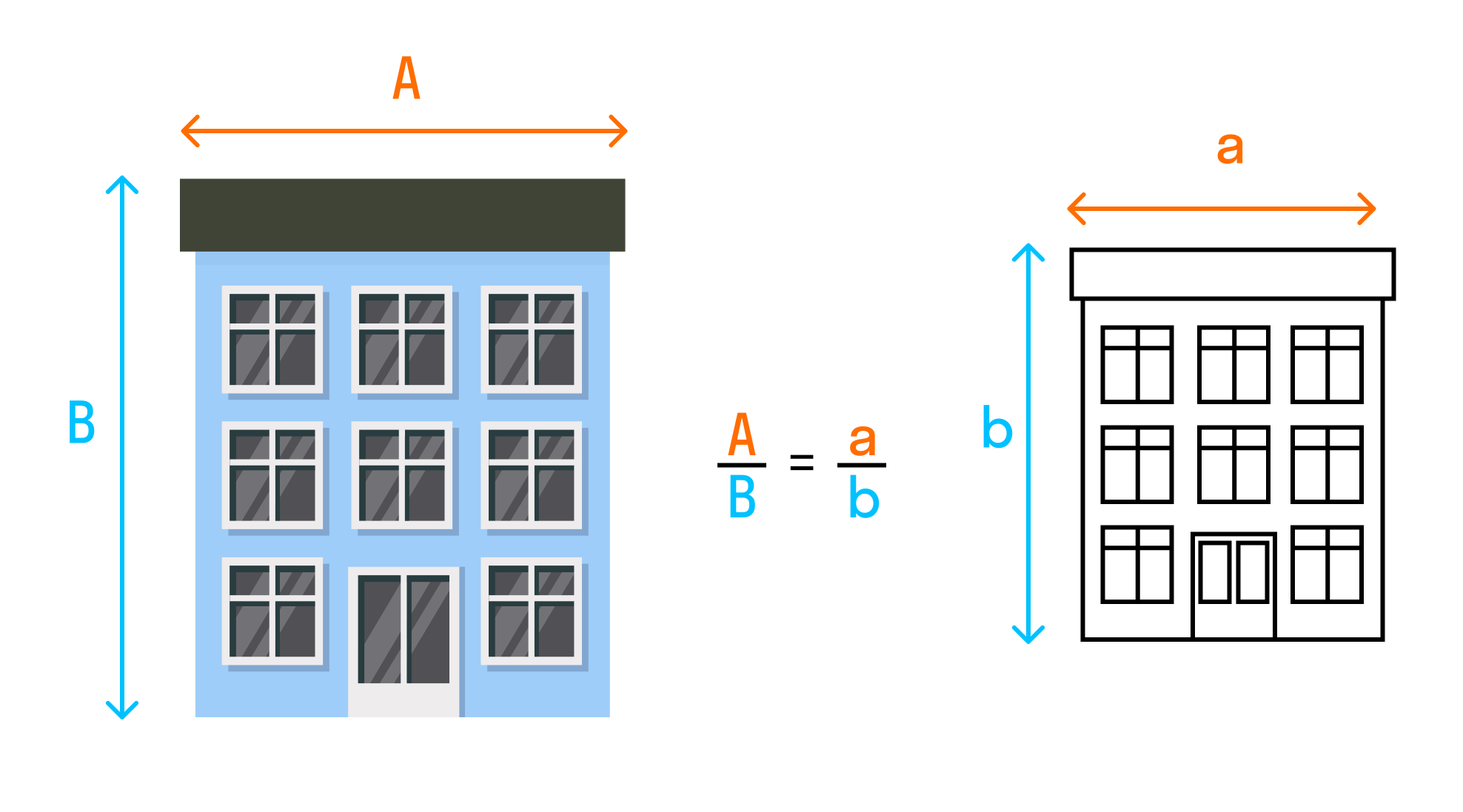
Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны.
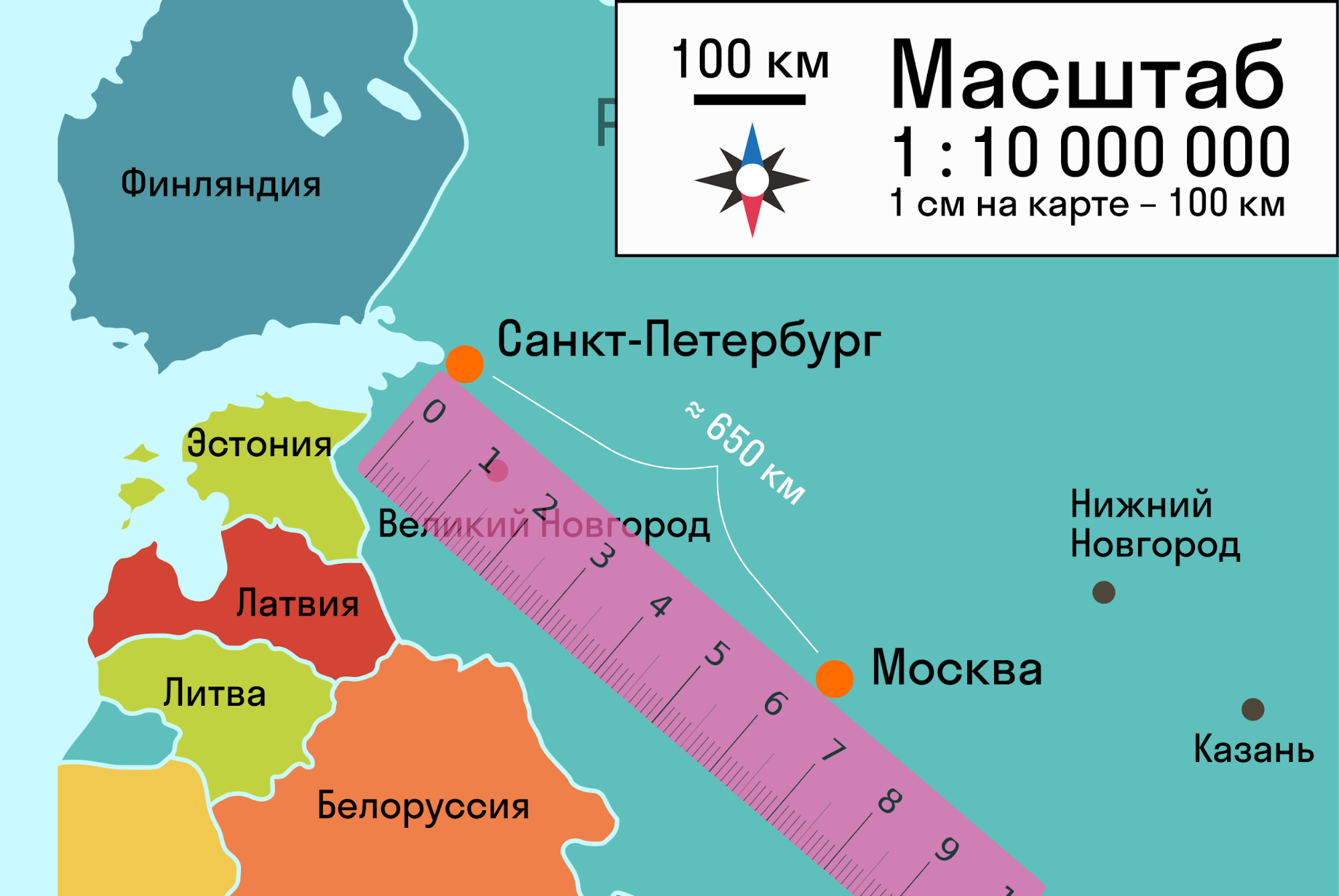
Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.
Классификация треугольников по их сторонам
Для классификации треугольников можно использовать их типологию.
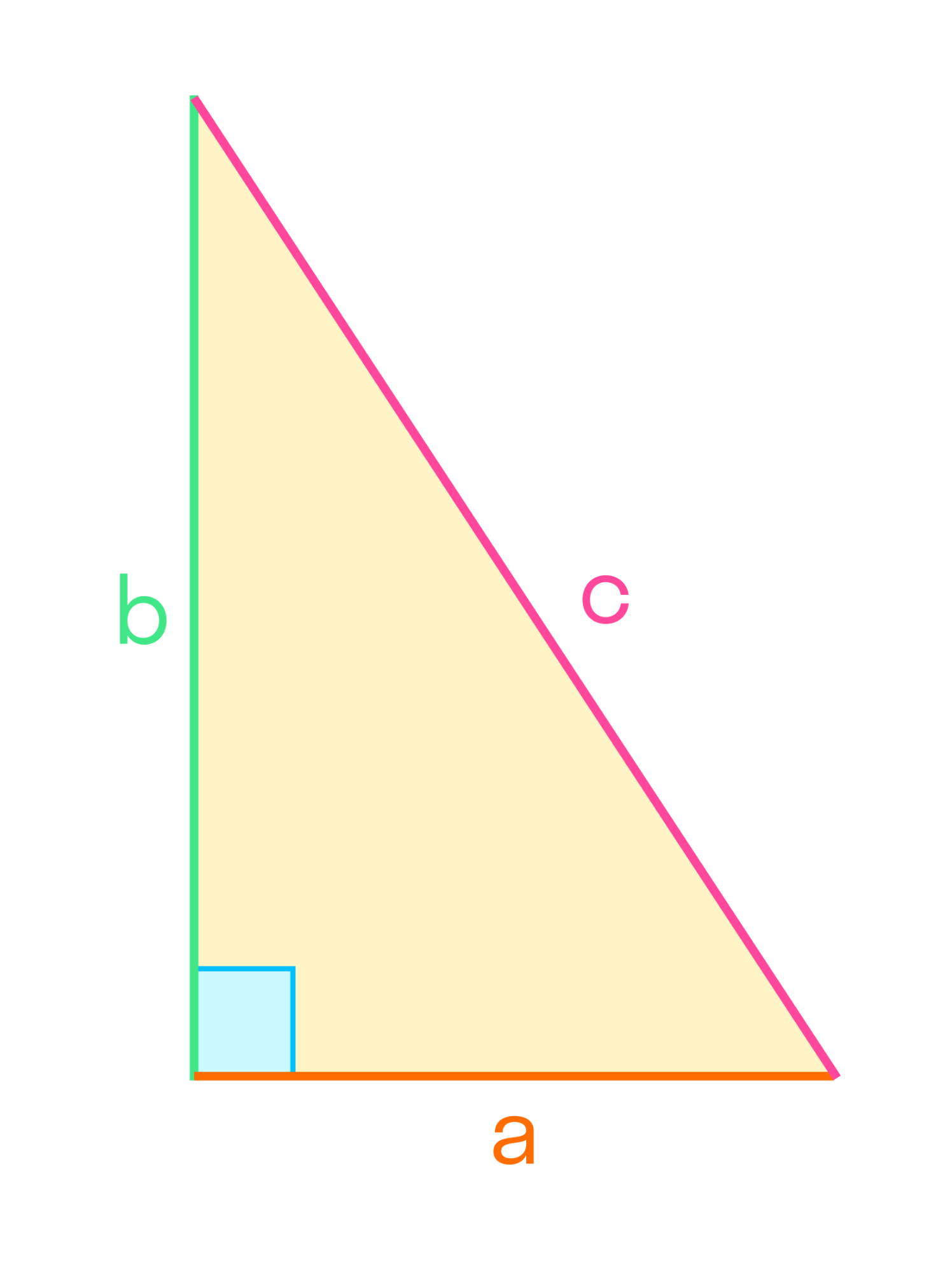
Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.
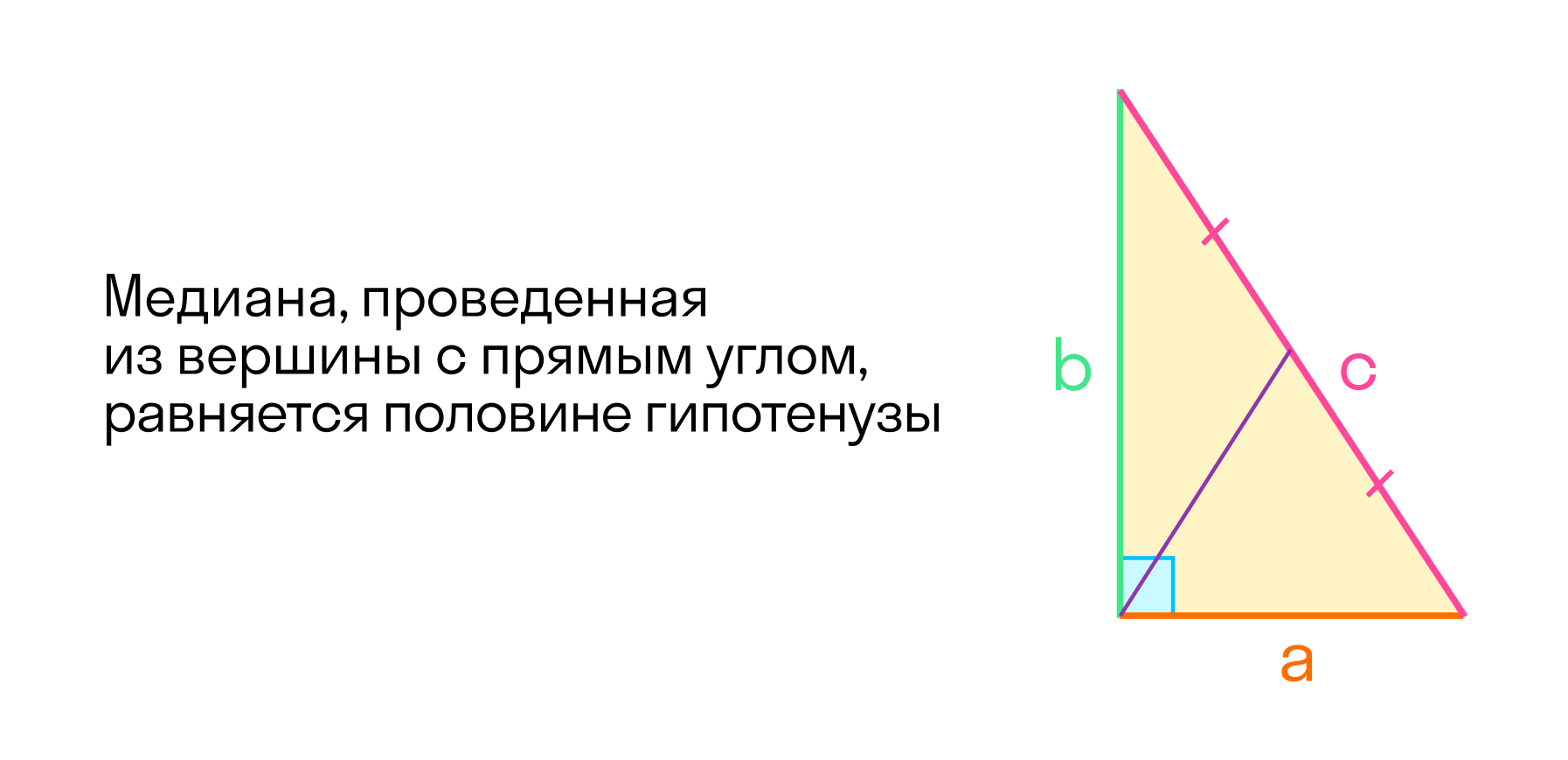
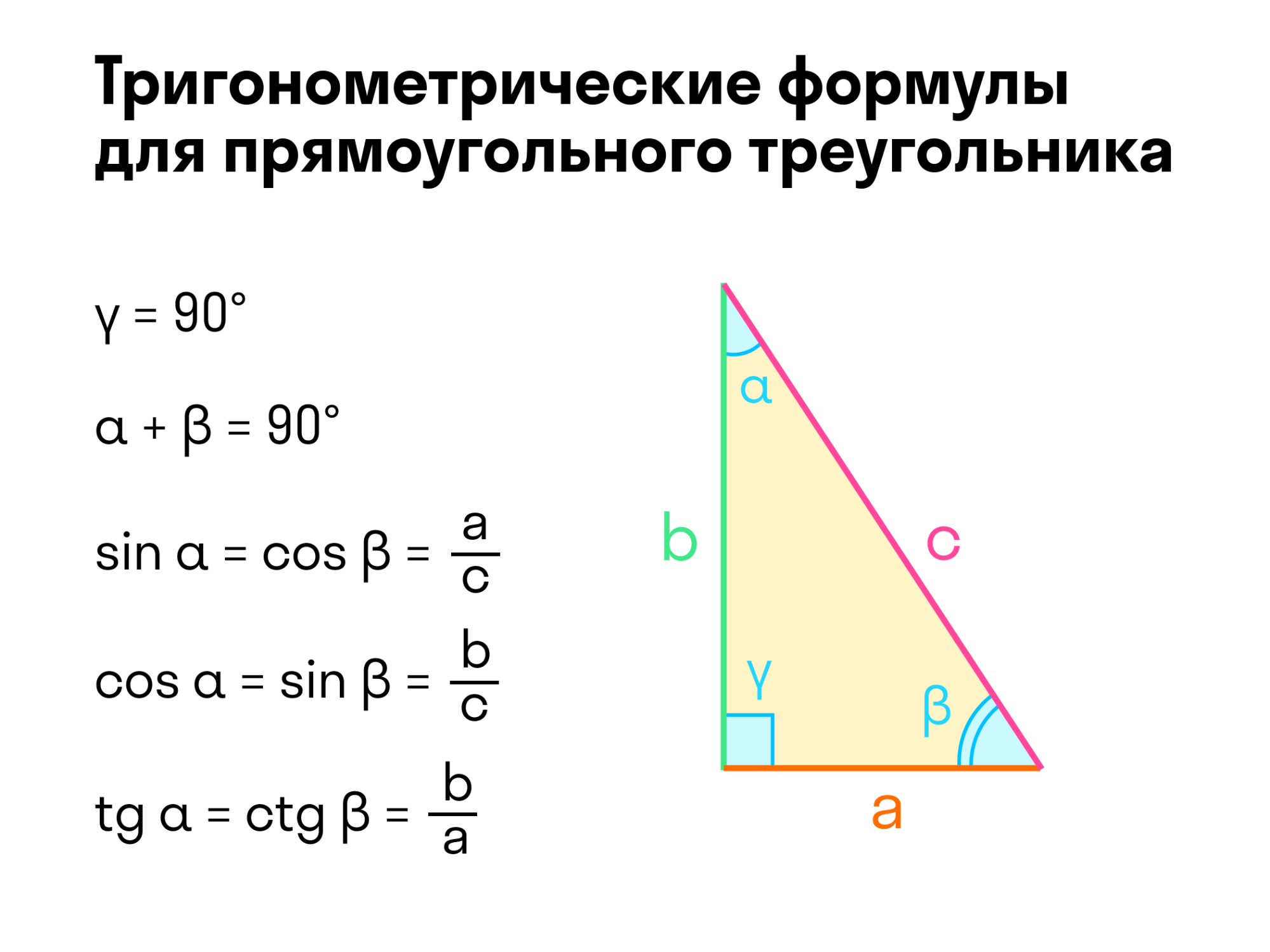
Свойства прямоугольного треугольника
С прямоугольных треугольников начинается изучение тригонометрии. Можно измерять углы с помощью отношений, использовать понятия синуса, косинуса. Помним, что угол можно задать двумя числами, их отношением.
Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.
Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.
Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.
От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃
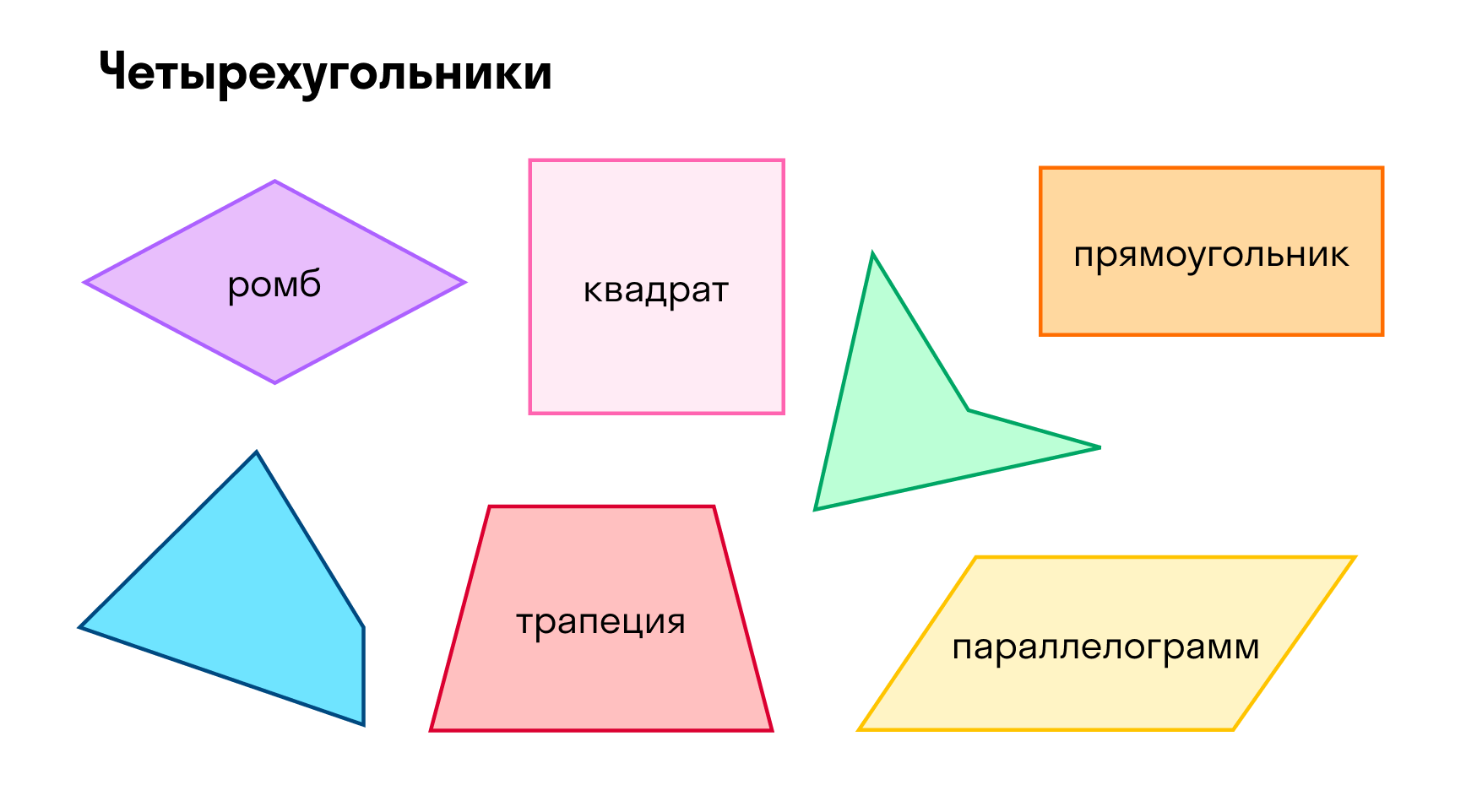
Четырехугольники
Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.
Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:
Окружность
Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Взаимодействие объектов
Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.
Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.
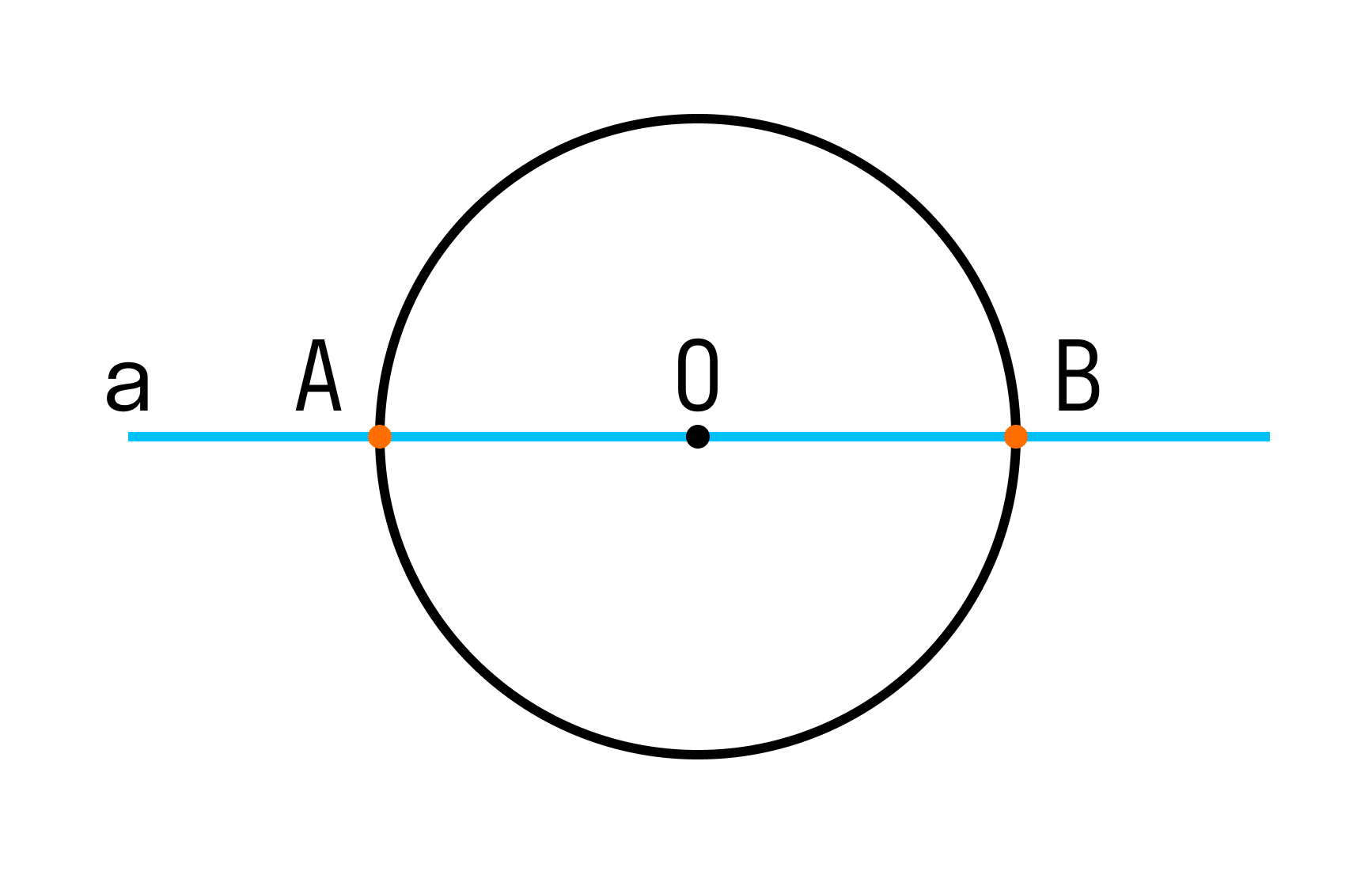
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.
На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.
Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a. Вот эти случаи:
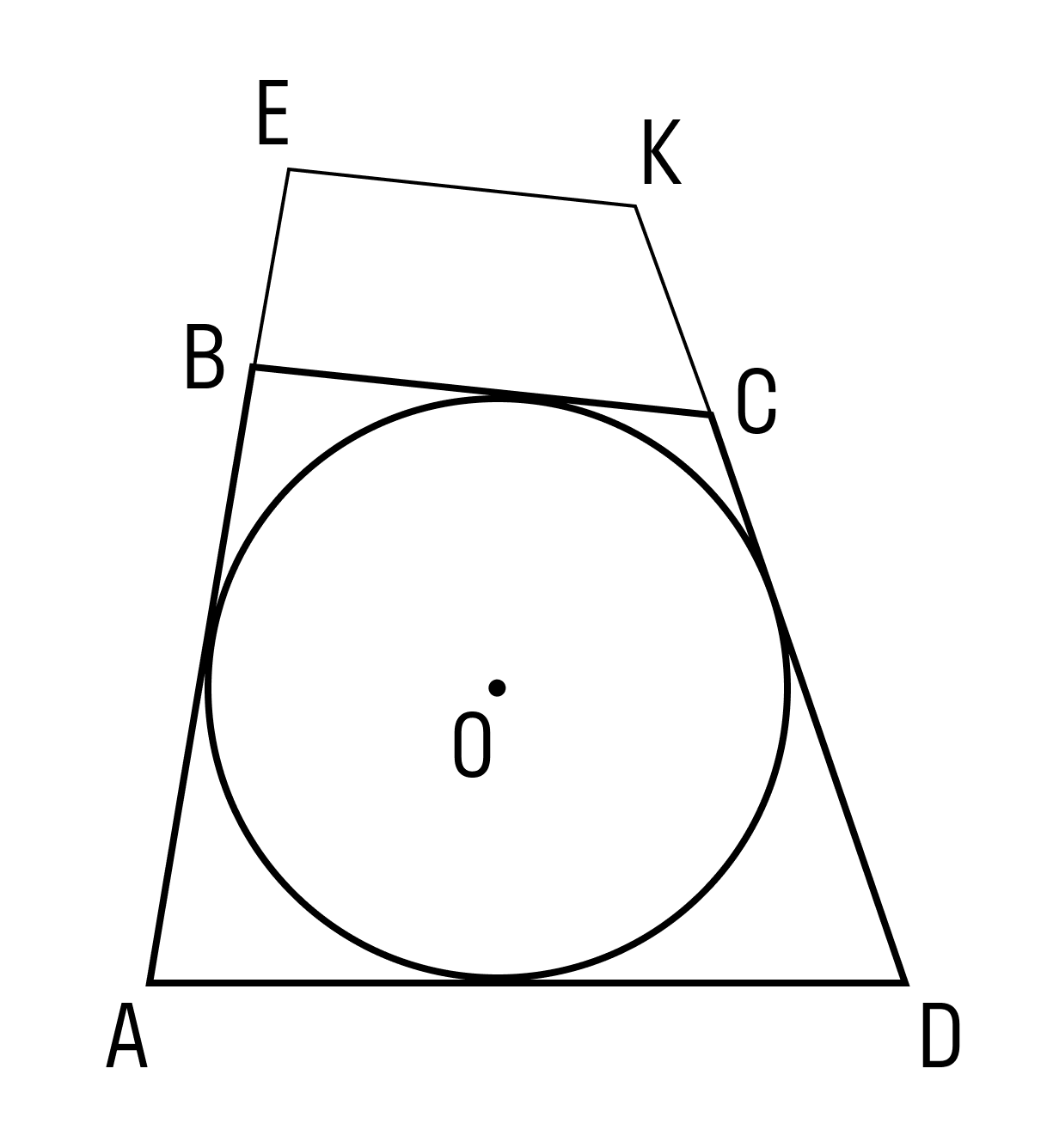
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.
На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.
В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.
Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила.
Практическая сторона геометрии
Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.
Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.
А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.
Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.
Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.
Почему изучать геометрию сложно: некоторые правила придется учить наизусть.
Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.