Презентация по информатике на тему: «Математическое моделирование с использованием электронных таблиц» (8 класс)

Описание презентации по отдельным слайдам:

Математическое моделирование с использованием электронных таблиц

Математическое моделирование Математическая модель – это описание моделируемого процесса на языке математики. Реальную систему, для которой создается математическая модель, принято называть объектом моделирования.

Реализованная на компьютере математическая модель называется компьютерной математической моделью. Проведение расчетов с помощью компьютерной модели с целью прогнозирования поведения моделируемой системы называется вычислительным экспериментом.

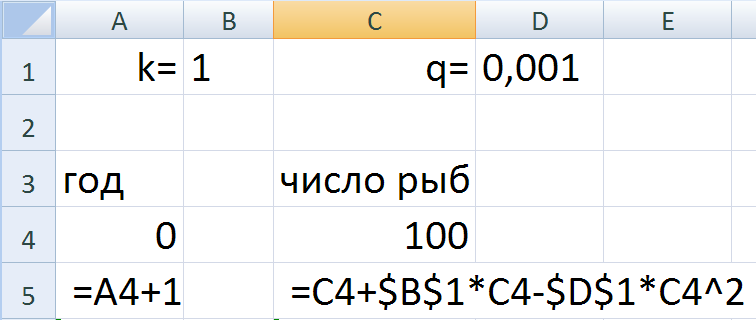
Лабораторная работа В одном хозяйстве собираются разводить карпов. Прежде чем запускать мальков в пруд, решили провести расчеты. N-число карпов в начале года k- коэффициент прироста q-коэффициент смертности

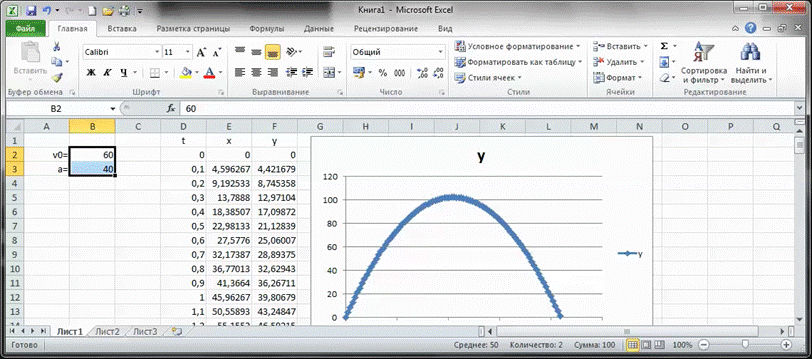
Теперь можно экспериментировать. Проследим как за 10 лет будет меняться число карпов при разном количестве первоначально запущенных рыб. Какой вывод можно сделать?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС

Курс повышения квалификации

Современные педтехнологии в деятельности учителя

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1625688

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России стартует пилотный проект по реабилитации детей-инвалидов

Время чтения: 2 минуты

Итоговое сочинение успешно написали более 97% выпускников школ

Время чтения: 2 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Российские юниоры завоевали 6 медалей на Международной научной олимпиаде

Время чтения: 2 минуты

В Госдуме проверят содержание учебников русского языка как иностранного

Время чтения: 2 минуты

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Знаковые модели. Компьютерные математические модели

Урок 4. Информатика 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Знаковые модели. Компьютерные математические модели»

· Определение компьютерной математической модели.

· Использование компьютерной математических моделей.

· Применение при решении задач.

Самые разные математические модели широко использовались и используются при изучении многих научных областей и дисциплин. Так, на пример, учёные астрономы используют математические модели, чтобы предсказать движение небесных тел. Как мы уже знаем, при составлении любых информационных моделей учитываются существенные свойства объекта или явления. Но что делать, если этих свойств очень много или они очень сложны для расчёта? Ведь человеку понадобится немало времени для реализации такой математической модели.

Реализация – это расчёт состояния объекта или системы, по формулам из математической модели, которые связывают значения его исходных и результирующих параметров.

Это одна из важнейших областей применения компьютеров. Ведь компьютер способен выполнять миллионы математических операций в секунду.

Математические модели, реализованные на компьютере с помощью тех или иных программных средств, называются компьютерными математическими моделями.

Для реализации математических моделей на компьютере могут использоваться:

· различные языки программирования,

· различные математические пакеты.

При использовании некоторых средств визуализации можно наглядно представить результаты и процесс работы той или иной системы.

Реализация математической модели в Microsoft Excel

После того, как математическая модель была задана достаточно нескольких нажатий клавиш, чтобы изменить исходные данные системы. И мы тут же получили результирующие данные для системы с другими параметрами.

Особую роль среди компьютерных математических моделей занимают модели систем, параметры которых могут принимать случайные значения в определённых пределах. Часто для того, чтобы оптимизировать работу такой системы, моделируют её работу при различных параметрах и находят их оптимальные значения. Такая математическая модель называется имитационной.

Имитационные модели применяются во многих сферах жизни человека. Например, моделирование системы обслуживания покупателей в магазине, чтобы выяснить, какое количество продавцов необходимо для нормальной его работы. Ведь мы не можем точно предсказать количество покупателей, пришедших в магазин за единицу времени или точное время обслуживания продавцом каждого из них.

Подобные модели могут применяться во многих областях науки. Рассмотрим пример из теории вероятности. Хорошо известно, что вероятность выпадения герба или цифры при подбрасывании монеты равна 50%, но как это проверить? Можно много раз подбросить монету, записывая результат. При этом очевидно, что чем большее число подбрасываний мы совершим, тем результат будет точнее. Некоторые математики проделывали этот опыт. Результаты некоторые результаты представлены в таблице.

Источник

Использование электронных таблиц MS Excel для компьютерного моделирования

Учебно-методическое обеспечение: презентация (Презентация), ПО MS Excel, ПО MS PowerPoint, методические указания.

Оборудование: мультимедийная установка, персональные компьютеры.

Ход конференции

Преподаватель: Межпредметное значение информатики в значительной степени проявляется именно через внедрение компьютерного моделирования в различные научные и прикладные области: математику и физику, технику, биологию и медицину, экономику, управление и многие другие. С помощью компьютерного моделирования решаются многие научные и производственные задачи. Гибким инструментом для компьютерного моделирования является MS Excel.

Возможности электронных таблиц Microsoft Excel весьма многогранны. Всем известно, что Excel является мощным вычислительным инструментом, позволяющим производить простые и сложные расчеты в различных областях человеческой деятельности: математике, физике, инженерных науках, экономике, технологии. На этом уроке мы рассмотрим использование электронных таблиц для решения математических задач и уравнений.

Теоретическая часть

Преподаватель: Рассмотрим этапы информационного моделирования.

Пусть вам надо решить какую-либо задачу, и вы хотите воспользоваться для этого помощью компьютера. С чего начать? Прежде всего, нужно разобраться, что дано, что требуется получить, как связаны исходные данные и результаты. Предположения, которые позволяют в море информации об изучаемом явлении или объекте определить исходные данные, понять, что будет служить результатом и какова связь между исходными данными и результатом, называют моделью задачи. (Презентация. Слайд 2)

2. Понятие математической модели.

В моделировании есть два различных пути. Во-первых, это использование натурных моделей. Но если модель должна отображать реальность в абстрактной форме, то в таком случае всегда привлекаются средства математики, и мы имеем дело с математической моделью.

Математическая модель выражает существенные признаки объекта или процесса языком уравнений и других математических средств. (Презентация. Слайд 3)

Собственно говоря, в историческом аспекте сама математика обязана своим существованием тому, что пыталась отражать, т.е. моделировать, на своем специфическом языке закономерности окружающего мира.

Под математической моделью понимают систему математических соотношений – формул, уравнений, неравенств и т.д., отражающих существенные свойства объекта или процесса. (Презентация. Слайд 3)

Математическое моделирование в наше время гораздо более всеобъемлющее, нежели моделирование натурное. Математический аппарат для моделирования объектов и процессов реального мира ученые использовали очень давно, но огромный толчок математическому моделированию дало появление ЭВМ, которые сегодня помогают в этой деятельности. Использование математического моделирования – это самый общий метод научных исследований.

Простой пример. Представьте, что нужно определить площадь поверхности письменного стола. Как обычно поступают в таком случае? Измеряют длину и ширину стола, а затем перемножают полученные числа. Это фактически означает, что реальный объект – поверхность стола – заменяется абстрактной математической моделью – прямоугольником. Площадь этого прямоугольника и считается искомой величиной.

Как видно, из всех свойств стола мы выделили три: форму поверхности (прямоугольник) и длины двух сторон. Для нас не важны ни цвет стола, ни материал, из которого он сделан, ни то, как стол используется. (Если бы мы решали другую задачу о столе, например, сколько стоит его изготовление, то возможно, для нас важна была бы как раз эта информация.) (Презентация. Слайд 4)

Предположив, что поверхность стола – прямоугольник, мы легко указываем исходные данные и находим результат. Они связаны соотношение S = a * b. (Презентация. Слайд 5)

Сделанное предположение позволило «перевести» нашу задачу на язык чисел: и исходные данные, и результат – числа, а соотношение между ними задается математической формулой.

Анализировать математические модели проще и быстрее, чем экспериментально определять поведение реального объекта. Кроме того, анализ математической модели позволяет выделить наиболее существенные свойства данного объекта (процесса), на которые надо обратить внимание при принятии решения.

3. Этапы решения задач на компьютере.

1 этап. Постановка задачи – точная формулировка условий и целей решения, описание наиболее существенных свойств объекта. (Презентация. Слайд 6)

2 этап. Построение математической модели – описание наиболее существенных свойств объекта с помощью математических формул. (Презентация. Слайд 6)

3 этап. Создание компьютерной модели – выражение математической модели на понятном для компьютера языке. Существуют два принципиально различных пути построения компьютерной модели:

4 этап. Проведение компьютерного эксперимента (исследование модели) – если компьютерная модель существует в виде программы на одном из языков программирования, то её нужно запустить на выполнение и получить результаты; если компьютерная модель исследуется в приложении, например, в электронных таблицах, можно провести сортировку или поиск данных, построить диаграмму или график и т.д. (Презентация. Слайд 8)

5 этап. Анализ полученных результатов и корректировка модели – в случае различия результатов, полученных при исследовании модели, с измеряемыми параметрами реальных объектов можно сделать вывод, что на предыдущих этапах построения модели были допущены ошибки или неточности. В этом случае необходимо провести корректировку модели, причём уточнение модели может проводиться многократно, пока анализ результатов не покажет их соответствие изучаемому объекту. (Презентация. Слайд 9)

Рассмотрим конкретные задачи математического моделирования. Для этого будем использовать приложение Windows – электронные таблицы MS Excel. Для этих целей в Excel имеется много возможностей: вычисление по формулам, построение диаграмм и графиков, поиск решения, подбор параметра и т.д.

Практическая часть

Задача 1. Необходимо покрасить краской стены кухни. Сколько потребуется банок краски, если известно, что

a = 405 см – длина комнаты,
b = 310 см – ширина комнаты,
c = 285 см – высота комнаты,
1 – 0,88 = 0,12 – часть комнаты для покраски (без кафеля),
5 м 2 – площадь покраски при использовании 1 банки краски.

Найти: необходимое для покраски стен кухни количество банок краски. (Презентация. Слайд 11)

S_{стен с кафелем} =2(a + b)c.
S_{стен для покраски} = 2(a + b)c * 0,12.

Моделирование в среде ЭТ.

Заносим данные задачи в электронную таблицу, вводим формулы.
Электронная таблица в режиме отображения формул. (Приложение 1. Презентация. Слайд 12)
Электронная таблица в режиме отображения значений. (Приложение 2. Презентация. Слайд 13)
С помощью MS Excel мы определили, что для покраски стен кухни необходима 1 банка краски.

Задача 2. Через иллюминатор корабля требуется вытащить сундук с драгоценностями. Удастся ли это сделать?

Иллюминатор корабля имеет форму круга. Будем считать, что сундук имеет форму параллелепипеда. Чтобы вытащить сундук, необходимо, чтобы диаметр иллюминатора был больше любой из трех диагоналей поверхности сундука. (Презентация. Слайд 14)

Пусть r – радиус иллюминатора,
a, b, c – размеры сундука,
d1, d2, d3 – диагонали боковых поверхностей сундука. (Презентация. Слайд 15)

Сундук можно вытаскивать через иллюминатор одной из трех боковых граней, следовательно, достаточно, чтобы диагональ иллюминатора оказалась меньше одной из трех диагоналей сундука, т.е. должно быть истинно хотя бы одно из условий:

ЕСЛИ((2*R>КОРЕНЬ(a^2+b^2));1;0)
ЕСЛИ((2*R>КОРЕНЬ(a^2+c^2));1;0)
ЕСЛИ((2*R>КОРЕНЬ(с^2+b^2));1;0)

(Презентация. Слайд 16)

Моделирование в среде ЭТ.

Заносим данные задачи в электронную таблицу, вводим формулы.
Электронная таблица в режиме отображения формул. (Приложение 3. Презентация. Слайд 17)
Электронная таблица в режиме отображения значений. (Приложение 4.Презентация. Слайд 18)

В электронной таблице находим сумму трех условий. Если сумма равна 0, делаем вывод «Сокровища недоступны», иначе «Сокровища доступны» (Слайд 19 Презентация).

Задача 3. Решить уравнение х4-4х3-10х2+37х-14=0 (Слайд 20 Презентация).

Необходимо построить график функции у = х 4 – 4х 3 – 10х 2 + 37х – 14. Точки пересечения графика с осью Х будут решениями данного уравнения. Составляем в MS Excel таблицу значений функции. (Приложение 5. Презентация. Слайд 21)

Построим график функции (диаграмму). (Приложение 5. Презентация. Слайд 22)

Мы видим, что график четырежды пересекает ось ОХ, значит уравнение х 4 – 4х 3 – 10х 2 + 37х –14 = 0 имеет четыре корня.

Из таблицы и графика можно определить промежутки, в которых находятся корни этого уравнения:

х₁ [–3,5; –3], х₂ [0; 0,5], х₃ [2; 2,5], х₄ [4,5; 5].

(Презентация. Слайд 23)

В первой строке указан адрес выбранного значения функции. Во второй нужно установить курсор и занести подбираемое значение функции, указанное в правой части данного уравнения (в нашем случае – число 0). А затем, установив курсор в третьей строке, надо щелкнуть мышью на ячейке с соответствующим значением аргумента, чтобы получить абсолютное значение этого адреса, затем щелкнуть ОК.

Аналогично проверяются корни из других промежутков.

Из результирующей таблицы выбираем корни уравнения. (Приложение 5. Презентация. Слайд 24)

Преподаватель: С особым вниманием следует применять этот способ для решения уравнений, у которых графики функции не являются так называемыми «гладкими» кривыми. Это касается, прежде всего, шага изменения аргумента при построении графика соответствующей функции: он не должен быть слишком большим, чтобы не пропустить значения некоторых корней.

Поясним это на примере решения уравнения.

Задача 4. Решить уравнение log₂(x(1 – x)) – sin(π/x) + 2 = 0, область определения которого: x принадлежит промежутку (0;1). (Презентация. Слайд 25)

Если построить график соответствующей функции в области ее определения с шагом h = 0,04, то получится один результат (Приложение 6. Презентация. Слайд 27), но если построить тот же график с меньшим шагом h = 0,01, то мы получим иной результат. (Приложение 6. Презентация. Слайд 27) Сравнение этих графиков показывает, что в первом случае из-за слишком большого шага «потеряны» два первых корня. Всего же рассматриваемое уравнение имеет шесть корней, которые уточняются с помощью Подбора параметра. (Презентация. Слайд 28)

Вывод. (Презентация. Слайд 29)

Источник

Компьютерные математические модели

Многие процессы, происходящие в окружающем нас мире, описываются очень сложными математическими соотношениями (уравнениями, неравенствами, системами уравнений и неравенств). До появления компьютеров, обладающих высокой скоростью вычислений, у человека не было возможности проводить соответствующие вычисления, на счёт «вручную» уходило очень много времени.

Математические модели, реализованные с помощью систем программирования, электронных таблиц, специализированных математических пакетов и программных средств для моделирования, называются компьютерными математическими моделями.

Средства компьютерной графики позволяют визуализировать результаты расчётов, получаемых в процессе работы с компьютерными моделями.

С помощью ресурса «Демонстрационная математическая модель» (119324) вы сможете смоделировать полёт снаряда, выпущенного из пушки при различных исходных данных (http://sc.edu.ru/).

Особый интерес для компьютерного математического моделирования представляют сложные системы, элементы которых могут вести себя случайным образом. Примерами таких систем являются многочисленные системы массового обслуживания: билетные кассы, торговые предприятия, ремонтные мастерские, служба «Скорой помощи», транспортные потоки на городских дорогах и многие другие модели. Многим знакома ситуация, когда, придя в кассу, магазин, парикмахерскую, мы застаём там очередь. Приходится либо вставать в очередь и какое-то время ждать, либо уходить, т. е. покидать систему необслу- женным. Возможны случаи, когда заявок на обслуживание в системе мало или совсем нет; в этом случае она работает с недогрузкой или простаивает. В системах массового обслуживания количество заявок на обслуживание, время ожидания и точное время выполнения заявки заранее предсказать нельзя — это случайные величины.

Имитационные модели воспроизводят поведение сложных систем, элементы которых могут вести себя случайным образом.

Имитационное моделирование — это искусственный эксперимент, при котором вместо проведения натурных испытаний с реальным оборудованием проводят опыты с помощью компьютерных моделей. Для получения необходимой информации осуществляется многократный «прогон» моделей со случайными исходными данными, генерируемыми компьютером. В результате образуется такой же набор данных, который можно было бы получить при проведении опытов на реальном оборудовании или в реальной системе. Однако имитационное моделирование на компьютере осуществляется гораздо быстрее и обходится значительно дешевле, чем натурные эксперименты.

С помощью ресурса «Демонстрационная имитационная модель» (119425) вы сможете смоделировать ситуацию в системе массового обслуживания — магазине (http://sc.edu.ru/).

САМОЕ ГЛАВНОЕ Словесные модели — это описания предметов, явлений, событий, процессов на естественных языках. Информационные модели, построенные с использованием математических понятий и формул, называются математическими моделями. Математические модели, реализованные с помощью систем программирования, электронных таблиц, специализированных математических пакетов и программных средств для моделирования, называются компьютерными математическими моделями. Источник Электронные таблицы и математическое моделирование Урок составлен к учебнику по информатике Семакина И. Г. «Информатика и ИКТ», 9 класс. В архиве: конспект урока, раздаточный материал, презентация к уроку, а также образец электронной таблицы для проведения компьютерного эксперимента. Просмотр содержимого документа «Моделирование в ЭТ» Конспект урока по теме «Электронные таблицы и математическое моделирование». Автор: Брев Николай Александрович, учитель информатики и физики МОУ-гимназии г. Переславля-Залесского. организовать деятельность учащихся по созданию компьютерной модели в электронных таблицах, для практического использования в различных жизненных ситуациях. развивать практические навыки по составлению моделей в электронных таблицах; формировать межпредметные связи; развивать аналитические способности обучающихся, логическое и алгоритмическое мышление. способствовать обогащению внутреннего мира обучающихся; воспитывать чувство патриотизма; ответственное отношение к своему здоровью. Тип урока: усвоение новых знаний. Формы организации учебной деятельности: практическая работа с раздаточным материалом; самостоятельная практическая работа; Оборудование: Проектор, экран, ноутбук, компьютеры, раздаточный материал. Материал будет полезен учителям информатики и ИКТ, преподающим в 9 классе по учебнику Семакина. Математическая модель. Повторение. Основные этапы математического моделирования на компьютере. Построение математической модели. Постановка задачи. Практическая работа. Реализация построенной математической модели на компьютере. Компьютерный эксперимент. Анализ полученных результатов. Обсуждение. Математическая модель. Повторение. конструкции, например, железнодорожный мост; природные объекты, например, водохранилище, процессы и явления, происходящие во времени, например взлет космической ракеты с космодрома, изменение погодных условий в определенной географической точке, изменение со временем численности определенных популяций. Для людей могут оказаться жизненно важными вопросы, связанные с этими объектами и процессами. Например: Какой может быть максимальная нагрузка на железнодорожный мост, при которой не будет происходить его разрушение? На какой высоте ракета достигнет первой космической скорости и выйдет на орбиту спутника Земли? Каким будет уровень воды в водохранилище в погодных условиях, которые предсказывают метеорологи? Не вымрет ли данная популяция животных через сто лет? На эти вопросы желательно получить ответы теоретическим путем, поскольку экспериментальный путь либо невозможен, либо опасен. Например, при перегрузке моста можно его разрушить, а экспериментально проверить, что будет с популяцией животных через сто лет, просто невозможно. В таких ситуациях на помощь человеку приходят математическое моделирование и вычислительный эксперимент. Основные этапы математического моделирования на компьютере. В математической модели используются количественные характеристики объекта (величины). Эти величины связываются между собой через уравнения, отражающие физические или другие законы. Из этих уравнений, зная одни величины (исходные данные), можно вычислить значения других величин (результатов). Часто такие расчеты бывает трудно осуществить вручную, и тогда используются компьютерные методы решения задачи. (Слайд 1) Реализованная на компьютере математическая модель называется компьютерной математической моделью, а проведение расчетов с помощью компьютерной модели с целью прогнозирования поведения моделируемой системы называется вычислительным экспериментом. Основные этапы компьютерного математического моделирования (Слайд 2) : Выделение количественных характеристик моделируемой системы, существенных для решаемой задачи. Получение математических соотношений (формул, уравнений, систем уравнений), связывающих эти характеристики. Определение способа решения полученной математической задачи и реализация ее на компьютере с помощью прикладных программных средств или на языках программирования. Решение поставленной задачи путем проведения вычислительного эксперимента. В результате вычислительного эксперимента можно получить прогноз поведения исследуемой системы; выяснить вопрос о том, как изменение одних характеристик системы отразится на других. Одним из видов прикладных программных средств, пригодных для реализации математической модели на компьютере, являются электронные таблицы. Построение математической модели. Постановка задачи. Чаще всего электронные таблицы используются для получения расчетных ведомостей, смет, справок, списков, т. е. в области делопроизводства. Однако электронные таблицы могут оказаться полезными и для научных целей. С их помощью можно строить компьютерные математические модели, проводить вычислительные эксперименты. Рассмотрим пример такого вычислительного эксперимента. Представьте, что у Вас есть собственное хозяйство, и Вы собираетесь разводить карпов. Прежде чем запускать мальков в пруд, решили провести расчеты. Согласно закону Мальтуса, изменение числа рыб за один год вычисляется по формуле Здесь N — число карпов в начале года, k — коэффициент прироста, q — коэффициент смертности. Экспериментально установлено, что для данного вида рыб (карпы) и в данных условиях (состояние водоема, наличие корма) k = 1, q = 0,001. (Слайд 4) Если первоначально в пруд запущено N 0 рыб, то из закона следует, что количество карпов через год будет таким: Можно написать общую формулу для вычисления количества рыб в i-м году после их запуска: Эта формула является математической моделью процесса размножения рыб в водоеме. (Слайд 6) Строки таблицы, начиная с 6-й, получаются путем копирования предыдущей строки. При этом относительные адреса изменяются автоматически. Для получения результатов нужно занести в ячейку С4 первоначальное число рыб (например, 100). Практическая работа. Реализация построенной математической модели на компьютере. Компьютерный эксперимент. Теперь можно экспериментировать. Необходимо Заполнить таблицу для проведения расчётов на 15 лет. По данным таблицы построить точечную диаграмму (с гладкими кривыми). Проследить, как будет меняться число карпов при различных значениях исходных данных . (Слайд 8) Анализ полученных результатов. Обсуждение. Теперь можно проанализировать полученные результаты: (Слайд 9) Растёт до 1000 и далее не изменяется. Сначала уменьшается, затем растёт до 1000. Через год все рыбы гибнут. Растёт до 1500 и далее не изменяется. Амплитуда периодических изменений резко увеличилась. Растёт, но до значения N Сначала уменьшается, а затем растёт и устанавливается на одном уровне. На уроке мы вспомнили, что называется математической моделью Математической моделью называется информационная модель объекта, выраженная математическими средствами (формулами, уравнениями и т. п.). Мы выяснили, что табличный процессор может применяться в качестве инструмента для математического моделирования, построили математическую модель для решения конкретной задачи Полученную математическую модель можно использовать для проведения вычислительного эксперимента. Проводя вычислительный эксперимент, мы выяснили, как будет меняться количество популяции в зависимости от начальных условий (количества рыб в водоёме, а также внешних условий (коэффициентов прироста и смертности). Просмотр содержимого документа «Раздаточный материал» Биологическая модель (закон Мальтуса). Практическая работа. Заполнить таблицу для проведения расчётов на 15 лет. По данным таблицы построить точечную диаграмму (с гладкими кривыми). Проследить, как будет меняться число карпов при различных значениях исходных данных. При изменении значения N 0 (500, 900, 1000, 1500, 1900, 2000) ; Источник ← Пневмопистолет для грузовых авто Как заплатить за квартиру через банкомат сбербанка → Вам также понравится С чего начать обследование спины 04.02.202403.07.2023 admin 0 я в поле вышел утром ранним 04.02.202414.07.2023 admin 0 С помощью чего открыть файл bmp 04.02.202403.07.2023 admin 0 Добавить комментарий Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев.