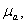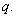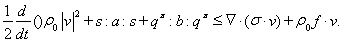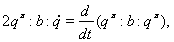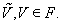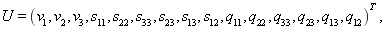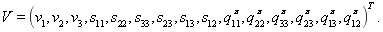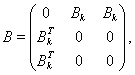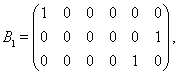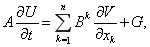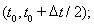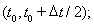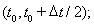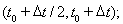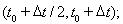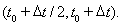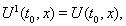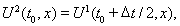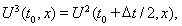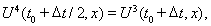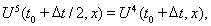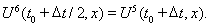сквозной счет что это
Метод сквозного счета для численного моделирования деформации пористых металлов
Дата публикации: 25.05.2016 2016-05-25
Статья просмотрена: 218 раз
Библиографическое описание:
Краснов, А. А. Метод сквозного счета для численного моделирования деформации пористых металлов / А. А. Краснов. — Текст : непосредственный // Молодой ученый. — 2016. — № 11 (115). — С. 35-40. — URL: https://moluch.ru/archive/115/29857/ (дата обращения: 11.12.2021).
Введение
В связи с возросшим интересом к новым материалам с перспективными свойствами, как с экономической, так и с механической точек зрения, большое значение имеет моделирование поведения различных сред под воздействием внешних сил. Металлические пены – представители целого семейства пористых материалов. Их отличительными свойствами являются низкая плотность и высокие прочностные характеристики [1, 2]. Причины, по которым пористые металлы еще не стали очень популярны, заключаются в несовершенстве технологии их производства (сложно получить однородное распределение пор) и высокой стоимостью этой технологии. В результате исследований последних лет наметились значительные изменения, как в совершенствовании методов получения металлических пен, так и в снижении стоимости их производства.
Технология
Получить пористые металлы можно несколькими способами [3]:
введением газа в жидкий сплав с образованием пузырьков нужного размера и их дальнейшей стабилизацией охлаждением;
формированием смеси из порошков металла и вспенивающего материала (например, 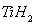
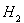
спеканием полых металлических сфер;
растворением газа в жидком металле под давлением, с контролируемым высвобождением в процессе затвердевания;
заполнением песком полимерного пористого материала с открытыми ячейками с дальнейшим выжиганием полимера и заполнением получившейся формы металлическим сплавом;
покрытием полимерного пористого материала с открытыми ячейками частицами металлического сплава методом электрического осаждения с последующим выжиганием полимера;
задержкой инертного газа в металлическом порошке под высоким давлением и дальнейшим нагреванием с расширением газа;
созданием смеси металла и растворяемого материала, с последующим выщелачиванием.
Все методы производства пористых металлов связаны с высокими температурами и необходимостью точно контролировать изменения температуры и давления на различных стадиях технологических процессов.
Модель
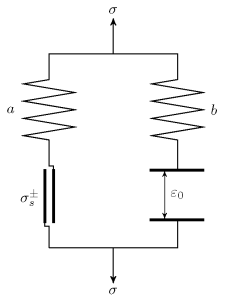
Для описания модели используется реологический метод. На рис. 1 приведена реологическая схема пористой среды [4]. Согласно этой схеме поведение пористого металла до момента схлопывания пор соответствует пружине с модулем упругой податливости 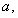
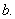
Рис. 1. Реологическая схема
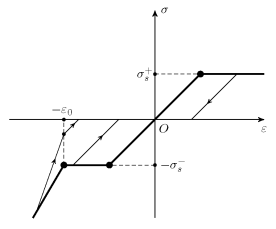
Диаграмма связи между напряжением и деформацией пористой среды при одноосном сжатии изображена на рис. 2.
Процесс упругой деформации материала описывается уравнением 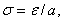
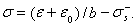
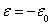
Используя приведенную выше реологическую схему можно составить следующие определяющие соотношения:
Здесь 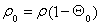
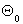
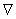
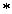
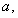
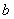
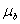
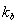
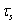
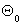
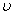
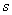
Рис. 2. Диаграмма связи между напряжением и деформацией
Полагая 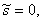
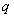
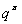
Левая часть неравенства представляет собой скорость изменения кинетической и потенциальной энергий, а правая – мощность внутренних поверхностных и активных объемных сил. Разность между правой и левой частями равна скорости пластической диссипации энергии, которая в соответствии с принципами необратимой термодинамики не может быть отрицательной величиной. При выводе данного неравенства существенно использовалось тождество [4]:
которое справедливо для проекции на произвольный выпуклый конус.
Вычислительный алгоритм
Чтобы построить алгоритм численной реализации описанной модели, представим соотношения (1) в виде вариационного неравенства в матричной форме:
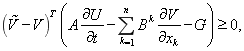
Здесь 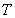
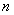
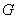
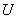
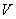
Матрицы-коэффициенты из вариационного неравенства (2) представимы следующим образом:
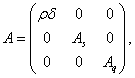
где 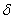
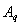

При 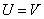
Для решения задачи деформирования пористой среды использован явный по времени алгоритм численной реализации метода сквозного счета с использованием метода расщепления по физическим процессам. На каждом шаге по времени решается задача деформирования упругой пористой среды:
используя метод двуциклического расщепления по пространственным переменным [7]. Для трехмерного случая на интервале 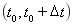
решение одномерной задачи в направлении 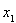
решение одномерной задачи в направлении 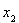
решение одномерной задачи в направлении 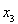
повторный пересчет в направлении 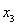
повторный пересчет в направлении 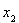
повторный пересчет в направлении 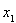
Расщепление системы уравнений (3) дает несколько одномерных систем:
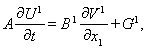
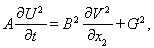
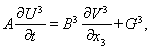
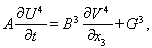
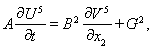
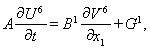
Искомое 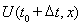
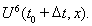
Чтобы учесть пластические свойства металла, вариационное неравенство (2) заменой производной по времени конечной разностью на интервале 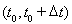
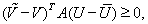
где 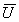
Параллельная реализация алгоритма
Расчеты проводятся на многопроцессорной вычислительной системе. Программирование выполнено по технологии SPMD (Single Program – Multiple Data) на языке Fortran-90 с использованием библиотеки MPI (Message Passing Interface). Программа выполняет подобные вычисления, сведенные к согласованной поэтапной реализации метода расщепления по пространственным переменным. Программная реализация алгоритма осложняется необходимостью склейки решений на границах разделения области между вычислительными узлами.
Вычисления выполняются для моделирования деформации блока пористого алюминия с различными значениями пористости 
1. Banhart J., Baumeister J. Deformation Characteristics of Metal Foams // Journal of Materials Science. – 1998. – Vol. 33, Iss. 6. – P. 1431–1440.
2. Gibson L.J., Ashby M.F. Cellular Solids: Structure and Properties, Second Edition // (ISBN: 978-0-521-49911-9). CambridgeUniversity Press, 1997.
3. Gibson L.J. Mechanical Behavior of Metallic Foams // Annual Review of Materials Research. – 2000. – Vol. 30. – P. 191–227.
4. Садовская О.В., Садовский В.М. Математическоемоделированиевзадачахмеханикисыпучихсред. – М.: Физматлит, 2008.
5. Ashby M.F. Plastic Deformation of Cellular Materials. Encyclopedia of Materials: Science and Technology (ISBN: 978-0-08-043152-9). PergamonPress. – 2001. – P. 7068–7071.
6. Золотухин А.В. Численное моделирование свойств пористых металлов // Материалы Всероссийской научно-практической конференции «Актуальные проблемы авиации и космонавтики». – Красноярск: СибГАУ. – 2011. – Т. 1. – С. 138–139.
7. Марчук Г.И. Методы расщепления. – М.: Наука, 1988.
Большая Энциклопедия Нефти и Газа
Методы сквозного счета позволяют рассчитывать течения без выделения разрывов, обладают простой логикой и требуют меньших затрат машинного времени, однако, они размазывают скачки, что снижает точность их расчета. Одними из наиболее распространенных методов этой группы являются метод искусственной вязкости ( метод Рихтмайера) и метод Лакса-Вендроффа. [1]
Методы сквозного счета для уравнений эллиптического и параболического типов в классе разрывных коэффициентов разработаны на основе интегро-интерполяционного метода А. Н. Тихоновым, А. А. Самарским [4] и другими. [2]
В методах сквозного счета разрыв не выделяется, и весь расчет проводится по единой схеме, что весьма выгодно при организации вычислений на компьютере. Разностные схемы, используемые для таких расчетов, называются однородными. Однако в этих схемах разрыв перестает быть разрывом в смысле изменения решения в одной точке. [3]
В методах сквозного счета разрыв не выделяется, и весь расчет проводится по единой схеме, что весьма выгодно при организации вычислений на ЭВМ. Разностные схемы, используемые для таких расчетов, называются однородными. Однако в этих схемах разрыв перестает быть разрывом в смысле изменения решения в одной точке. [5]
В методах сквозного счета ( shock-capturing methods) производные аппроксимируются и через разрывы. При этом разрыв размазывается на отрезке, величина которого определяется численной диссипацией разностной схемы, и превращается в узкую область с резкими перепадами значений сеточных функций. Ширина такого перехода обычно уменьшается с увеличением порядка точности разностной схемы. При использовании сквозного счета в областях больших перепадов сеточных величин могут возникать нефизические осцилляции, которые должны быть каким-либо образом устранены. [6]
Применения такого метода сквозного счета позволяет получать практически точные решения одномерных задач газовой динамики при полном отсутствии размазывания одиночных тангенциальных разрывов и ударных волн, так как дискретная сетка автоматически подстраивается к ним в процессе счета. Все это делает данный подход сравнимым с методами, основанными на выделении разрывов. К тому же его можно дополнительно использовать для обнаружения разрывов, которые возникают с течением времени из гладких начальных условий. [7]
При использовании некоторого метода сквозного счета получились значения сеточной функции, отмеченные точками. [9]
С другой стороны, методы сквозного счета могут достичь точности методов выделения плавающих разрывов только при использовании расчетных сеток, адаптированных к большим градиентам решения. [11]
Что представляет транзитный счёт в банке
Организациям и физлицам, занимающимся предпринимательской деятельностью, в рамках банковского обслуживания может открываться расчетный счет, валютный счет для операций, соответственно, в рублях и иностранной валюте. Что собой представляет транзитный счет и почему, в отличие от валютного, он не выделяется в плане счетов бухгалтерского учета? Расскажем об особенностях транзитных счетов и их назначении.
Вопрос: В банк поступило постановление судебного пристава-исполнителя о наложении ареста на денежные средства на транзитном счете, открытом банком для расчетов между должником и третьими лицами. Вправе ли банк отказать в исполнении такого постановления?
Посмотреть ответ
Особенности транзитного счета
Суть любого банковского счета одна и та же. Это учетная запись банка, на которой отражаются операции клиентов с денежными средствами. Отличие транзитного счета в том, что он всегда связан с другим – валютным и самостоятельно не используется. Он предназначен прежде всего для перечисления валютных сумм и имеет контрольное значение.
Одновременное открытие двух взаимосвязанных счетов прописано в законодательстве для резидентов – участников внешнеэкономической деятельности (ВЭД):
Кстати говоря! Понятие «резидент» в валютном законодательстве определяется статьей 1-1 пп. 6 ФЗ-173. К ним относятся, в частности, российские фирмы и компании, их филиалы, представительства за границей, индивидуальные предприниматели – физлица. Иные юридические и физические лица относятся к нерезидентам (п. 7).
Как открыть транзитный счет
Эта операция не зависит от желания владельца валютного счета. Открытие «в паре» с ним транзитного счета – обязанность банка. Об этом сказано в инструкции №111-И, п. 2.1. Каждому валютному счету, открываемому по видам валют, соответствует отдельный транзитный счет. Действия банка с транзитным счетом клиента — участника ВЭД — связаны с правом банка контролировать валютные операции.
Раньше транзитный счет использовался для контроля обязательного объема продаж валютной выручки на внутреннем рынке валюты РФ. Этот норматив с 30% год от года снижался и в настоящее время составляет 0% (Инструкция 111-И п. 1.2), т.е., по сути, об обязательной продаже выручки в валюте речи не идет.
Транзитный счет нужен только для контроля валютных операций как таковых. Законность сделки клиент подтверждает документами, информацией о коде вида операции. При этом, если в рублевом эквиваленте сумма не выше 200 тыс. руб., достаточно информации о коде вида операции. Если сумма выше, банк потребует и документы. Срок предоставления – 15 рабочих дней. Процедура контроля подробно описана в инструкции ЦБ РФ №181-И от 16/08/17.
После проверки банк может запросить дополнительную информацию по сделке, если возникли сомнения в ее законности, либо списать средства на текущий счет клиента на основе имеющейся информации. В исключительных случаях средства на транзитном счете могут быть заблокированы.
Перечисление на текущий счет (валютный или расчетный с обменом на рубли) происходит по письменному распоряжению клиента.
Что и как отражают на счете
На транзитном счете отражается вся валютная выручка в пользу российской компании или ИП, а списываются средства на текущие счета резидентов.
Операции по транзитному счету отражаются в бухучете на счете 52 «Валютные счета». Можно пользоваться счетом 52 с/счет 1 «Валютные счета внутри страны» с открытием аналитического счета «Транзитный валютный счет в банке» (план счетов для с/х предприятий, приказ Минсельхоза №654 от 13/06/01). Специалисты предлагают и другой вариант: открыть два субсчета – текущий валютный счет, транзитный валютный счет и использовать их в проводках. Проводки формируются с использованием счета 76 либо 57 «Переводы в пути».
Пример отражения стандартных операций:
Либо такой вариант:
Не все валютные средства проходят через транзитный счет, часть попадает сразу на действующий валютный счет:
Отметим, что в инструкции №111-И (гл. 2 п. 2.3.1) говорится о списании средств с транзитного счета в целях обязательной продажи части валютной выручки. Как мы уже говорили, норма продажи на сегодняшний день составляет 0%. (гл. 1 п. 1.2 того же документа). Кроме того, упоминается об уменьшении суммы обязательной продажи на сумму расходов и платежей, связанных с исполнением сделок (п. 1.3), однако следует отсылка к ст. 21 ФЗ-173. Эта статья в настоящее время не действует.
метод сквозного счета
Смотреть что такое «метод сквозного счета» в других словарях:
Метод Годунова — Метод Годунова реализация схем сквозного счета, с помощью которых можно рассчитывать газодинамические течения с разрывами параметров внутри расчётной области. Метод Годунова это вариант метода контрольного объёма. Потоки через боковые … Википедия
ГАЗОВОЙ ДИНАМИКИ ЧИСЛЕННЫЕ МЕТОДЫ — методы решения задач газовой динамики на основе вычислительных алгоритмов. Рассмотрим основные аспекты теории численных методов решения задач газовой динамики, записав газовой динамики уравнения в виде законов сохранения в инерциальной… … Математическая энциклопедия
РАЗНОСТНЫХ СХЕМ ТЕОРИЯ — раздел вычислительной математики, изучающий методы приближенного решения дифференциальных уравнений путем их замены конечноразностными уравнениями (р а з н о с т н ы м и с х е м а м и). Р. с. т. изучает способы построения разностных схем,… … Математическая энциклопедия
ГИПЕРБОЛИЧЕСКОГО ТИПА УРАВНЕНИЕ — численные методы решения методы решения уравнений гииерболпч. типа на основе вычислительных алгоритмов. Различные математич. модели во многих случаях приводят к дифференциальным уравнениям гиперболич. типа. Такие уравнения имеют точные аиалитич.… … Математическая энциклопедия
характеристика — 3.1 характеристика (characteristic): Качественное или количественное свойство элемента. Примечание Примеры характеристик давление, температура, напряжение. Источник: ГОСТ Р 51901.11 2005: Менеджмент риска. Исследование опасности и… … Словарь-справочник терминов нормативно-технической документации
Холдинг — (Holding) Определение холдинга, типы холдига, холдинговые компании Информация об определении холдинга, типы холдига, холдинговые компании Содержание Содержание Характерные черты холдинга Типы холдинга Холдинговые Проблемы банковских холдингов… … Энциклопедия инвестора