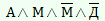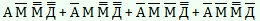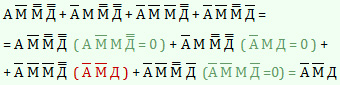в некотором царстве государстве повадился змей горыныч разбойничать послал царь четырех богатырей
КТО ИЗ БОГАТЫРЕЙ ПОБЕДИЛ ЗМЕЯ ГОРЫНЫЧА?
Решение логических задач средствами алгебры логики
Условие задачи:
В некотором царстве-государстве повадился Змей Горыныч разбойничать. Послал царь четырёх богатырей погубить Змея. Награду за то обещал великую. Вернулись богатыри с победой, и спрашивает их царь: «Так кто же из вас главный победитель, кому достанется царёва дочь и полцарства?».
Засмущались, добры молодцы и ответы дали туманные:
Сказал Илья Муромец: «Это всё Алёша Попович, царь-батюшка»;
Алёша Попович возразил: «То был Микула Селянинович»;
Микула Селянинович: «Не прав Алёша, не я то»;
Добрыня Никитич: «И не я, царь-батюшка».
Подвернулась тут Баба-Яга и говорит царю:
«А прав-то лишь один из богатырей, видела я всю битву своими глазами».
Кто же из богатырей победил Змея Горыныча?
§ Интересности о Змее Горыныче 😉 читайте на зелёной страничке «Экскурсия по драконьему царству».
Решение задачи:
«Переводим» условие задачи на язык алгебры логики 😉
1. Определяемся с системой обозначений для логических высказываний:
А – Алёша Попович;
М – Микула Селянинович;
Д – Добрыня Никитич.
Илья Муромец первым перед царём-батюшкой слово держал, но про него никто ничего не сказал 🙂
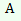 | «Это всё Алёша Попович, царь-батюшка» – это Алёша Попович |
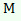 | «То был Микула Селянинович» – это МикулаСелянинович |
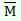 | «Не прав Алёша, не я то» – это не Микула Селянинович |
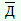 | «И не я, царь-батюшка» – это не Добрыня Никитич |
Сведём выше сказанное в единое целое (логическая связка «И»):
Учитывая слова Бабы-Яги:
«А прав-то лишь один из богатырей, видела я всю битву своими глазами»:
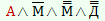 | Правду сказал Илья Муромец |
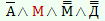 | Правду сказал Алёша Попович |
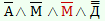 | Правду сказал Микула Селянинович |
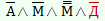 | Правду сказал Добрыня Никитич |
Лирическое отступление 😉 алгебра логики
∧ – знак логического умножения (конъюнкция) – соединение высказываний с помощью союза «И» (AND). X∧Y; X&Y; X·Y или XY. Где: « ∧ », « & », « · » – знаки, обозначающие операцию логического умножения. Все варианты записи равнозначны. В решении нашей задачи для облегчения восприятия итоговой формулы я использую вариант записи логического умножения «XY».
∨ – знак логического сложения (дизъюнкция) – соединение высказываний с помощью союза «ИЛИ» (OR). X∨Y; X + Y. Где: « ∨ », « + » – знаки, обозначающие операцию логического сложения. Оба варианта записи равнозначны. В решении нашей задачи я использую вариант записи логического сложения «X + Y».
Некоторые операции и законы алгебры логики, необходимые для решения нашей задачи:
2. Конструируем итоговую логическую формулу, описывающую логические связи между всеми высказываниями условия задачи. По условию нашей задачи прав только один из богатырей (логическая связка «ИЛИ»):
3. Определяем значения истинности логической формулы. Упрощаем формулу. Используем операции и законы алгебры логики и учитываем, что по условию нашей задачи: А ∧ М = 0; А ∧ Д = 0; М ∧ Д = 0
Ответ: Змея Горыныча победил Добрыня Никитич!
В копилочку для веб-мастера 😉 спецсимволы HTML:
| ∧ | ∧ или ∧ | логическое умножение «И» (конъюнкция) |
| ∨ | ∨ или ∨ | логическое сложение «ИЛИ» (дизъюнкция) |
§ Греческий алфавит на HTML с указанием произношения букв
для тех, кто вращается на орбитах астрономии, математики, физики 😉
§ Способы умножения без таблицы умножения (гимнастика для ума)
русский способ умножения; рисовательный способ умножения 🙂
некоторые математические символы на HTML
Для тех, кто любит учиться! Для тех, кому в радость гимнастика для ума 😉
§ Решение логических задач табличным способом
Былинная русская живопись
Виктор Михайлович Васнецов (15.05.1848–23.07.1926) – русский живописец, график, иллюстратор и архитектор. Портретист, монументалист, автор жанровых картин, театральный художник. Мастер исторической и фольклорной живописи. Родоначальник «русского стиля» в рамках символизма, присущего европейскому искусству конца XIX века. В его творчестве соединились исторические мотивы с поэтической атмосферой сказок, оставив в русской и мировой культуре яркий след.
 |
 |
 |
 |
Полотно Виктора Михайловича Васнецова «Богатыри» – воплощение народной силы и могущества. Застава богатырская зорко охраняет русскую землю. В дозоре три богатыря – Илья Муромец, Добрыня Никитич и Алёша Попович – главные герои русских былин. Посередине на дородном вороном коне Илья Муромец, вглядывается в даль из под мускулистой руки, с которой свисает тяжёлая булатная палица, в другой руке острое копье наизготове. Слева от Ильи Муромца на белом коне Добрыня Никитич, вынимает меч из ножен. Справа на красно золотистом коне Алёша Попович, держит в руках лук со стрелами.
Богатыри изображены на фоне сурового степного пейзажа, их головы и плечи возвышаются над линией горизонта, отчего богатыри кажутся ещё более мощными и значительными. Симметричное расположение фигур, устойчивость композиции, намеренная скованность в их движениях (до поры до времени) передают сплочённость богатырей, объединённых общим стремлением – не пропустить врага в пределы Руси.
Степь покрыта густой ковыльной травой. Над дальней холмистой цепью возвышенностей с перелесками нависло низкое небо, покрытое холодными свинцовыми тучами. За холмами к северу – Русь, та широкая, раздольная Русь, которая вырастила и снарядила могучих богатырей на защиту своих границ от многочисленных орд кочевников.
Над картиной «Богатыри» Васнецов работал в течение двадцати с лишним лет, с карандашного наброска 1871 года до момента, когда в 1898 году подписал, наконец, своё произведение.
Микулы Селяниновича на полотне Васнецова нет. По той причине, что прославился этот русский богатырь не ратным подвигом, а трудовым. Микула Селянинович – пахарь-богатырь в русских былинах. Он олицетворяет крестьянскую силу; биться с ним нельзя, так как «весь род Микулов любит Матушка Сыра Земля».
Кузнецов Николай Дмитриевич (02.12.1850–02.03.1850) – русский портретный и жанровый живописец, профессор Императорской Академии художеств, член Товарищества передвижных художественных выставок.
 | ||||
 |
На картине «Иван Царевич на сером волке» воспроизведён эпизод из сказки об Иване-Царевиче, Жар-Птице и о Сером Волке, изложенной А.Н. Афанасьевым по тексту из лубочного издания XVIII века. Стремясь открыть зрителю красоту и возвышенность мира народной фантазии, передать народные представления о красоте и счастье, Виктор Михайлович Васнецов использовал символическое значение образов народной поэзии.
На полотне исполинские стволы деревьев тёмного непроходимого леса похожи на фантастических великанов. Сквозь переплетённые ветви деревьев-чудовищ едва пробивается тревожный свет утренней зари. Таит опасность топкое болото с кувшинками. Героев окружает атмосфера тревоги и печали – беглецов ждут несчастья и разлука. А на первом плане – чудесно расцветшее яблоневое дерево – символ всепобеждающей любви, способной творить чудеса, знак счастливого конца сказки.
§ Картина Ильи Ефимовича Репина «Садко» – первая в былинной русской живописи. Смотрите на зелёной страничке «Путешествие по зелёному цвету».
Очень трогательная, явно чем-то расстроенная… Баба-Яга на картине «Леший и Баба-Яга» в исполнении Николая Сергеевича Сергеева.
 |
 |
Сергеев Николай Сергеевич (1908–1989) – советский художник, живописец, график.
Экстравагантная Баба-Яга с роскошными седыми космами в нарядном красном сарафане… в окружении русалок… в исполнении современной российской художницы Светланы Петровны Голубечковой.
 |
 |
§ «Баба-Яга в ступе» – иллюстрация Ивана Билибина к русской народной сказке «Василиса Прекрасная» на зелёной страничке «Иван Яковлевич Билибин (иллюстрации к русским сказкам)».
Логические задачи для самостоятельного решения:
Задача №1
Внимание Олега, Дениса и Максима привлёк промчавшийся мимо автомобиль.
– Это английская машина марки «Ferrari», – сказал Олег.
– Нет, машина итальянская марки «Pontiac», – возразил Денис.
– Это «Saab», и сделан он не в Англии, – сказал Максим.
Оказавшийся рядом знаток автомобилей сказал, что каждый из них прав только в одном из высказанных предположений.
Какой же марки этот автомобиль, и в какой стране он изготовлен?
Задача №2
В клуб служебного собаководства на очередную тренировку пришли со своими собаками Антон, Богдан, Пётр, Дмитрий и Олег. Желая подшутить над новым инструктором, на его вопрос: «Кто же хозяин каждой из собак?», каждый юноша дал один правильный и один неправильный ответ.
Антон сказал: «Моя собака – Рекс, а собака Петра – Лайма».
Богдан сказал: «Рекс – моя собака, а собака Дмитрия – Джек».
Пётр сказал: «Собака Дмитрия Зевс, а моя – Рекс».
Дмитрий сказал: «Моя собака – Джек, а собака Олега – Бичо».
Олег сказал: «Да моя собака – Бичо, а собака Богдана – Зевс».
Кто же на самом деле хозяин каждой из собак?
Задача №3
В ходе археологических раскопок в Олимпии студенты-практиканты Московского Государственного Университета имени М.В. Ломоносова Александр, Тарас и Станислав нашли в земле старинный сосуд. Рассматривая находку, каждый высказал по два предположения:
Александр: «Это сосуд греческий и изготовлен в V веке».
Тарас: «Это сосуд финикийский и изготовлен в III веке».
Станислав: «Это сосуд не греческий и изготовлен в IV веке».
Эксперты установили, что каждый из них прав только в одном из двух предположения.
Где и в каком веке изготовлен сосуд?
Литература:
§ Монахов В.М. Программирование. Факультативный курс
Москва: издательство «Просвещение», 1974
§ Деге В. Waldemar Dege (перевод с немецкого) ЭВМ думает, считает, управляет
Москва: издательство «Мир», 1974
§ Ерофеев Ю.Н. Импульсные устройства
Москва: издательство «Высшая школа», 1989
§ Шауцукова Л.З. Информатика. Учебное пособие
Москва: издательство «Просвещение», 2000
Замечательная статья. Логическая задачка очень интересная!
Картина «Богатыри» Васнецова это бесценнейший бриллиант былинной русской живописи! Сильная картина!
«Баба-Яга» Голубечковой действительно красотка, а не женщина!
Согласен с Димой на все 100.
Недавно читали с дочкой стихи Эдуарда Успенского.
Нашёл в сети и рад поделиться:
Про Бабу-Ягу говорят очень глупо:
Нога костяная, метёлка да ступа.
И руки кривые, и зубы торчком,
И нос очень длинный и загнут крючком.
Я облик сложившийся быстро разрушу:
Прошу заглянуть в мою чистую душу.
И там вы такие откроете дали,
Каких никогда и нигде не видали.
В душе я добра, хороша, справедлива.
Не так чтобы очень, но всё же красива.
И в каждом я только хорошее вижу,
Я даже козявку в душе не обижу.
Но если внутри я добра и прекрасна,
То сверху, снаружи, хитра и опасна.
Я в жизни любого из вас одолею,
А то и убью. Но в душе пожалею.
§ Алиса в лесу Забывчивости
Решение логических задач методом рассуждений
«Из ложных посылок можно вывести истинное заключение».
Аристотель
§ Загадка Эйнштейна, а может быть и Кэрролла на новый лад 😉
Решение логических задач табличным способом
«Если бы это было так, это бы ещё ничего, а если бы ничего, оно бы так и было, но так как это не так, так оно и не этак! Такова логика вещей!».
Льюис Кэрролл
§ Одноклассницы на встрече выпускников
Решение логических задач табличным способом
«Поиски прекрасного приводят нас к тому же выбору, что и поиски полезного».
Жюль Анри Пуанкаре
§ Три дочери писательницы Жаклин Деманж
Решение логических задач табличным способом
«Логика, которая одна может дать достоверность, есть орудие доказательства; интуиция есть орудие изобретательства».
Жюль Анри Пуанкаре
§ Способы умножения без таблицы умножения (гимнастика для ума)
Посвящается Елене Петровне Каринской,
моему школьному преподавателю математики и классному руководителю
Алма-Ата, РОФМШ, 1984–1987 год
Русский способ умножения; рисовательный способ умножения 🙂
Некоторые математические символы на HTML
§ Программирование: Заочная школа Delphi 7.0
Закладка Additional компонент StringGrid. Таблицы истинности.
Решение задач с помощью алгебры высказываний
Решение задач с помощью алгебры высказываний
Решение задач с помощью алгебры высказываний
Отношение логического следования используется при исследовании рассуждений.
Решение:
Данное высказывание тавтологией не является, значит из указанных посылок не следует высказывание «6 – составное число».
Решение:
Решение:
$$( H\vee S )\And \bar H\rightarrow S\equiv ( \bar H\And \bar S )\vee H\vee S\equiv ( H\vee \bar H )\And ( \bar S\vee H )\vee S\equiv \bar S\vee H ∨ S\equiv 1$$
Значит, высказывание «я останусь и выпью» является логическим следствием из данных посылок.
Задача 4. В некотором царстве-государстве повадился Змей Горыныч разбойничать. Послал царь четырёх богатырей погубить Змея. Награду за то обещал великую. Вернулись богатыри с победой, и спрашивает их царь: «Так кто же из вас главный победитель, кому достанется царёва дочь и полцарства?».
Засмущались, добры молодцы и ответы дали туманные:
Сказал Илья Муромец: «Это всё Алёша Попович, царь-батюшка»;
Алёша Попович возразил: «То был Микула Селянинович»;
Микула Селянинович: «Не прав Алёша, не я то»;
Добрыня Никитич: «И не я, царь-батюшка».
Подвернулась тут Баба-Яга и говорит царю: «А прав-то лишь один из богатырей, видела я всю битву своими глазами».
Кто же из богатырей победил Змея Горыныча?
Решение задачи:
Определяемся с системой обозначений для логических высказываний:
Илья Муромец первым перед царём-батюшкой слово держал, но про него никто ничего не сказал
Сведём выше сказанное в единое целое < логическая связка «И» >:
$$A\And M\And \bar M \And \bar D$$
Учитывая слова Бабы-Яги: «А прав-то лишь один из богатырей, видела я всю битву своими глазами»:
Конструируем итоговую логическую формулу, описывающую логические связи между всеми высказываниями условия задачи. По условию нашей задачи прав только один из богатырей < логическая связка «ИЛИ» >:
Определяем значения истинности логической формулы. Упрощаем формулу.
Ответ: Змея Горыныча победил Добрыня Никитич
Далее:
Механические приложения тройного интеграла
Функции k-значной логики. Элементарные функции. Лемма об аналоге правила де Моргана
Поток жидкости через поверхность
Вычисление поверхностного интеграла первого рода
Вычисление криволинейного интеграла первого рода. Плоский случай
Полином Жегалкина. Пример.
Теорема об алгоритме распознавания полноты
Теорема об аналоге СДНФ в Pk
Нормальные формы
Векторное поле
Критерий полноты <формулировка>. Лемма о несамодвойственной функции
Вычисление криволинейного интеграла второго рода. Примеры.
Свойства двойного интеграла
Замыкание. Свойства замыкания. Теорема о сведении к заведомо полной системе
В некотором царстве-государстве повадился Змей Горыныч разбойничать. Послал царь четырёх богатырей погубить Змея, а награду за то обещал великую. Вернулись богатыри с победой и спрашивает их царь: “Так кто же из вас главный победитель, кому достанется царёва дочь и полцарства?” Засмущались добры молодцы и ответы дали туманные: Сказал Илья Муромец: “Это все Алеша Попович, царь-батюшка”. Алеша Попович возразил: “То был Микула Селянинович”. Микула Селянинович: “Не прав Алеша, не я это”. Добрыня Никитич: “И не я, батюшка”. Подвернулась тут баба Яга и говорит царю: “А прав то лишь один из богатырей, видела я всю битву своими глазами”.
Кто же из богатырей победил Змея Горыныча?
«Переводим» условие задачи на язык алгебры логики 😉
1. Определяемся с системой обозначений для логических высказываний:
М – Микула Селянинович;
Д – Добрыня Никитич.
Илья Муромец первым перед царём-батюшкой слово держал, но про него никто ничего не сказал 🙂
«Это всё Алёша Попович, царь-батюшка» – это Алёша Попович«То был Микула Селянинович» – это МикулаСелянинович«Не прав Алёша, не я то» – это не Микула Селянинович«И не я, царь-батюшка» – это не Добрыня Никитич
Сведём выше сказанное в единое целое (логическая связка «И»):
Учитывая слова Бабы-Яги:
«А прав-то лишь один из богатырей, видела я всю битву своими глазами»:
Правду сказал Илья МуромецПравду сказал Алёша ПоповичПравду сказал Микула СеляниновичПравду сказал Добрыня Никитич
Лирическое отступление 😉 алгебра логики
∧ – знак логического умножения (конъюнкция) – соединение высказываний с помощью союза «И» (AND). X∧Y; X&Y; X·Y или XY. Где: « ∧ », « & », « · » – знаки, обозначающие операцию логического умножения. Все варианты записи равнозначны. В решении нашей задачи для облегчения восприятия итоговой формулы я использую вариант записи логического умножения «XY».
∨ – знак логического сложения (дизъюнкция) – соединение высказываний с помощью союза «ИЛИ» (OR). X∨Y; X + Y. Где: « ∨ », « + » – знаки, обозначающие операцию логического сложения. Оба варианта записи равнозначны. В решении нашей задачи я использую вариант записи логического сложения «X + Y».
Некоторые операции и законы алгебры логики, необходимые для решения нашей задачи:
закон двойного отрицания:
закон идемпотентности для конъюнкции:
операции с переменной и её инверсией:
2. Конструируем итоговую логическую формулу, описывающую логические связи между всеми высказываниями условия задачи. По условию нашей задачи прав только один из богатырей (логическая связка «ИЛИ»):
3. Определяем значения истинности логической формулы. Упрощаем формулу. Используем операции и законы алгебры логики и учитываем, что по условию нашей задачи: А ∧ М = 0; А ∧ Д = 0; М ∧ Д = 0
Ответ: Змея Горыныча победил Добрыня Никитич!
В некотором царстве-государстве повадился Змей Горыныч разбойничать. Послал царь четырех богатырей погубить Змея, а награду
Ответы 7
«Переводим» условие задачи на язык алгебры логики 😉
1. Определяемся с системой обозначений для логических высказываний:
М – Микула Селянинович;
Д – Добрыня Никитич.
Илья Муромец первым перед царём-батюшкой слово держал, но про него никто ничего не сказал 🙂
«Это всё Алёша Попович, царь-батюшка» – это Алёша Попович«То был Микула Селянинович» – это МикулаСелянинович«Не прав Алёша, не я то» – это не Микула Селянинович«И не я, царь-батюшка» – это не Добрыня Никитич
Сведём выше сказанное в единое целое (логическая связка «И»):
Учитывая слова Бабы-Яги:
«А прав-то лишь один из богатырей, видела я всю битву своими глазами»:
Правду сказал Илья МуромецПравду сказал Алёша ПоповичПравду сказал Микула СеляниновичПравду сказал Добрыня Никитич
Лирическое отступление 😉 алгебра логики
∧ – знак логического умножения (конъюнкция) – соединение высказываний с союза «И» (AND). X∧Y; X&Y; X·Y или XY. Где: « ∧ », « & », « · » – знаки, обозначающие операцию логического умножения. Все варианты записи равнозначны. В решении нашей задачи для облегчения восприятия итоговой формулы я использую вариант записи логического умножения «XY».
∨ – знак логического сложения (дизъюнкция) – соединение высказываний с союза «ИЛИ» (OR). X∨Y; X + Y. Где: « ∨ », « + » – знаки, обозначающие операцию логического сложения. Оба варианта записи равнозначны. В решении нашей задачи я использую вариант записи логического сложения «X + Y».
Некоторые операции и законы алгебры логики, необходимые для решения нашей задачи:
закон двойного отрицания:
закон идемпотентности для конъюнкции:
операции с переменной и её инверсией:
2. Конструируем итоговую логическую формулу, описывающую логические связи между всеми высказываниями условия задачи. По условию нашей задачи прав только один из богатырей (логическая связка «ИЛИ»):
3. Определяем значения истинности логической формулы. Упрощаем формулу. Используем операции и законы алгебры логики и учитываем, что по условию нашей задачи: А ∧ М = 0; А ∧ Д = 0; М ∧ Д = 0
ответ: Змея Горыныча победил Добрыня Никитич!