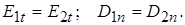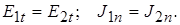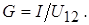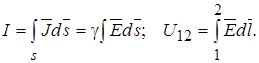электростатическое поле и электрическое поле разница
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Поле электростатическое и электрическое
2. При движении ионов в проводнике второго рода (в самом объёме раствора) возникает магнитное поле или же только вокруг проводника? (В приближении если говорить)
| Заслуженный участник |
Электрическое поле является электростатическим, только когда все заряды неподвижны, и нет переменных по времени электрических и магнитных полей.
Ни в чём, кроме того, что быстро закончится.
При любом протекании тока возникает магнитное поле везде в объёме (кроме сверхпроводников). Это просто видно из уравнения Максвелла 
Эта поляризация будет происходить всегда, при любой величине зарядов.
Последний раз редактировалось rambler87 05.03.2014, 12:56, всего редактировалось 1 раз.
Ещё такой, надеюсь пока последний, мысленный эксперимент.
Имеем две установки:
I. катод | проводник второго рода | анод
II. (-) стат.заряд | диэл. | проводник второго рода | диэл. | (+) стат. заряд
В первом случае через проводник второго рода потечёт постоянный ток
Во втором случае мы будем иметь временный ток пока происходит поляризация проводника да? То есть можно подобрать заряды статические так, чтобы никакой разницы между физическим состоянием проводника второго рода в первом и втором экспериментах не было. Пусть даже это продлится очень небольшой промежуток времени
| Заслуженный участник |
И наконец, всё то, о чём вы спрашиваете, совершенно не зависит от того, проводник какого рода обсуждается. Можно мысленно заменить электролит на металл, и получить тот же самый ответ, и он будет правильным.
Последний раз редактировалось rambler87 05.03.2014, 14:27, всего редактировалось 3 раз(а).
На самом деле мне этот мысленный эксперимент был нужен постольку, поскольку наличие различного рода электродных процессов усложняет картину.
| Заслуженный участник |
Ну, это уже никак не явления теории электричества, это сложные последствия биологического уровня.
На самом деле мне этот мысленный эксперимент был нужен постольку, поскольку наличие различного рода электродных процессов усложняет картину.

Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей
Что такое электрическое поле, его классификация и характеристики
Нас окружает материальный мир. Материю мы воспринимаем с помощью зрения и других органов чувств. Отдельным видом материи является электрическое поле, которое можно выявить только через его влияние на заряженные тела или с помощью приборов. Оно порождает магнитные поля и взаимодействует с ними. Эти взаимодействия нашли широкое практическое применение.
Определение
Электрическое поле неразрывно связано с магнитным полем, и возникает в результате его изменения. Эти два вида материи являются компонентами электромагнитных полей, заполняющих пространство вокруг заряженных частиц или заряженных тел.
Таким образом, данный термин означает особый вид материи, обладающий собственной энергией, являющийся составным компонентом векторного электромагнитного поля. У электрического поля нет границ, однако его силовое воздействие стремится к нулю, при удалении от источника – заряженного тела или точечных зарядов [1].
Важным свойством полевой формы материи является способность электрического поля поддерживать упорядоченное перемещение носителей зарядов.

Энергия электрического поля подчиняется действию закона сохранения. Её можно преобразовать в другие виды или направить на выполнение работы.
Силовой характеристикой полей выступает их напряжённость – векторная величина, численное значение которой определяется как отношение силы, действующей на пробный положительный заряд, к величине этого заряда.
Характерные физические свойства:
Оно всегда окружает неподвижные статичные (не меняющиеся со временем) заряды, поэтому получило название – электростатическое. Опыты подтверждают, что в электростатическом поле действуют такие же силы, как и в электрическом.
Электростатическое взаимодействие поля на заряженные тела можно наблюдать при поднесении наэлектризованной эбонитовой палочки к мелким предметам. В зависимости от полярности наэлектризованных частиц, они будут либо притягиваться, либо отталкиваться от палочки.
Сильные электростатические поля образуются вблизи мощных электрических разрядов. На поверхности проводника, оказавшегося в зоне действия разряда, происходит перераспределение зарядов.
Вследствие распределения зарядов проводник становится заряженным, что является признаком влияния электрического поля.
Классификация
Электрические поля бывают двух видов: однородные и неоднородные.
Однородное электрическое поле
Состояние поля определяется пространственным расположением линий напряжённости. Если векторы напряжённости идентичны по модулю и они при этом сонаправлены во всех точках пространства, то электрическое поле – однородно. В нём линии напряжённости расположены параллельно.
В качестве примера является электрическое поле, образованное разноимёнными зарядами на участке плоских металлических пластин (см. рис. 2).

Неоднородное электрическое поле
Чаще встречаются поля, напряжённости которых в разных точках отличаются. Линии напряжённости у них имеют сложную конфигурацию. Простейшим примером неоднородности является электрический диполь, то есть система из двух разноимённых зарядов, влияющих друг на друга (см. рис. 3). Несмотря на то, что векторы напряжённости электрического диполя образуют красивые линии, но поскольку они не равны, то такое поле неоднородно. Более сложную конфигурацию имеют вихревые поля (рис 4). Их неоднородность очевидна.


Характеристики
Основными характеристиками являются:
Потенциал
Термин означает отношение потенциальной энергии W, которой обладает пробный заряд q′ в данной точке к его величине. Выражение φ =W/q′. называется потенциалом электрического поля в этой точке.
Другими словами: количество накопленной энергии, которая потенциально может быть потрачена на выполнение работы, направленной на перемещение единичного заряда в бесконечность, или в другую точку с условно нулевой энергией, называется потенциалом рассматриваемого электрического поля в данной точке.
Энергия поля учитывается по отношению к данной точке. Её ещё называют потенциалом в данной точке. Общий потенциал системы равен сумме потенциалов отдельных зарядов. Это одна из важнейших характеристик поля. Потенциал можно сравнить с энергией сжатой пружины, которая при высвобождении способна выполнить определённую работу.
Единица измерения потенциала – 1 вольт. При бесконечном удалении точки от наэлектризованного тела, потенциал в этой точке уменьшается до 0: φ∞=0.
Напряжённость поля
Достоверно известно, что электрическое поле отдельно взятого заряда q действует с определённой силой F на точечный пробный заряд, независимо от того, на каком расстоянии он находится. Сила, действующая на изолированный положительный пробный заряд, называется напряжённостью и обозначается символом E.
Напряжённость – векторная величина. Значение модуля вектора напряжённости: E=F/q′.
Линиями напряжённости электрического поля (известные как силовые линии), называются касательные, которые в точках касания совпадают с ориентацией векторов напряжённости. Плотность силовых линий определяет величину напряжённости.

Напряженность вокруг точечного заряда Q на расстоянии r от него, определяется по закону Кулона: E = 14πε0⋅Qr2. Такие поля называют кулоновскими.
Векторы напряженности положительного точечного заряда направлены от него, а отрицательного – до центра (к заряду). Направления векторов кулоновского поля видно на рис. 6.

Для кулоновских полей справедлив принцип суперпозиции. Суть принципа в следующем:вектор напряжённости нескольких зарядов может быть представлен в виде геометрической суммы напряжённостей, создаваемых каждым отдельно взятым зарядом, входящих в эту систему.
Для общего случая распределения зарядов имеем:
Линии напряжённости схематически изображены на рисунке 7. На картинке видно линии, характерные для полей:
Напряжение
Поскольку силы электрического поля способны выполнять работу по перемещению носителей элементарных зарядов, то наличие поля является условием для существования электрического тока. Электроны и другие элементарные заряды всегда двигаются от точки, обладающей более высоким потенциалом, к точке с низшим потенциалом. При этом часть энергии расходуется на выполнение работы по перемещению.
Для поддержания постоянного тока (упорядоченного движения носителей элементарных зарядов) необходимо на концах проводника поддерживать разницу потенциалов, которую ещё называют напряжением. Чем больше эта разница, тем активнее выполняется работа, тем мощнее ток на этом участке. Функции по поддержанию разницы потенциалов возложены на источники тока.
Методы обнаружения
Органы чувств человека не воспринимают электрических полей. Поэтому мы не можем их увидеть, попробовать на вкус или определить по запаху. Единственное, что может ощутить человек – это выпрямление волос вдоль линий напряжённости. Наличие слабых воздействий мы просто не замечаем.
Обнаружить их можно через воздействие на мелкие кусочки бумаги, бузиновые шарики и т.п. Электрическое поле воздействует на электроскоп – его лепестки реагируют на такие воздействия.
Очень простой и эффективный метод обнаружения с помощью стрелки компаса. Она всегда располагается вдоль линий напряжённости.
Существуют очень чувствительные электронные приборы, с лёгкостью определяющие наличие электростатических полей.
Методы расчета электрического поля
Для расчётов параметров используются различные аналитические или численные методы:
Выбор конкретного метода зависит от сложности задачи, но в основном используются численные методы, приведённые в списке.
Использование
Изучение свойств электрического поля открыло перед человечеством огромные возможности. Способность поля перемещать электроны в проводнике позволила создавать источники тока.
На свойствах электрических полей создано различное оборудование, применяемое в медицине, химической промышленности, в электротехнике. Разрабатываются приборы, применяемые в сфере беспроводной передачи энергии к потребителю. Примером могут послужить устройства беспроводной зарядки гаджетов. Это пока только первые шаги на пути к передачи электричества на большие расстояния.
Сегодня, благодаря знаниям о свойствах полевой формы материи, разработаны уникальные фильтры для очистки воды. Этот способ оказался дешевле, чем использование традиционных сменных картриджей.
К сожалению, иногда приходится нейтрализовать силы полей. Обладая способностью электризации предметов, оказавшихся в зоне действия, электрические поля создают серьёзные препятствия для нормальной работы радиоэлектронной аппаратуры. Накопленное статическое электричество часто является причиной выхода из строя интегральных микросхем и полевых транзисторов.
Электростатическое поле и электрическое поле разница
123 дн. с момента
до конца учебного года
Электростатическое поле и его характеристики
Электростатическое поле существующий вокруг неподвижный заряженных тел, действует на заряд с некоторой силой, вблизи заряда – сильнее.
Электростатическое поле не изменяется во времени.
Силовой характеристикой электрического поля является напряженность
Напряженностью электрического поля в данной точке называется векторная физическая величина, численно равная силе, действующей на единичный положительный заряд, помещенный в данную точку поля.
Силовыми линиями (линиями напряженности электрического поля) называют линии, касательные к которым в каждой точке поля совпадают с направлением вектора напряженности в данной точке.
Силовые линии начинаются на положительном заряде и заканчиваются на отрицательном ( Силовые линии электростатических полей точечных зарядов. ).
Густота линий напряженности характеризует напряженность поля (чем плотнее располагаются линии, тем поле сильнее).
Электростатическое поле точечного заряда неоднородно (ближе к заряду поле сильнее).
Силовые линии электростатических полей бесконечных равномерно заряженных плоскостей.
Электростатическое поле бесконечных равномерно заряженных плоскостей однородно. Электрическое поле, напряженность во всех точках которого одинакова, называется однородным.
И электростатическим полем
Аналогия между полем в проводящей среде
По своей природе электростатическое поле и поле постоянного тока в проводящей среде различны. Электростатическое поле создается электрическими зарядами, неизменными во времени и неподвижными в пространстве. Электрическое поле в проводящей среде создается электрическими зарядами, которые имеют упорядоченное движение под действием внешнего источника. Однако между полями существует формальная аналогия.
Электростатическое поле в областях, не занятых зарядами удовлетворяет уравнению Лапласа. Этому же уравнению удовлетворяет электрическое поле постоянного тока в проводящей среде вне сторонних источников. В обоих случаях имеют дело с вектором напряженности электрического поля 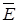
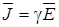
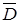
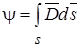
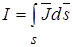
Граничные условия на поверхности раздела двух диэлектриков:
Граничные условия на поверхности раздела двух сред с различной проводимостью
Учитывая вышесказанное, можно сделать вывод, что при одинаковой форме граничных поверхностей картина поля в обоих случаях будет одинаковой (совокупность силовых и эквипотенциальных линий).
Соотношение между проводимостью и емкостью
Если какие-либо электроды поместить в проводящую среду и присоединить к источнику ЭДС, то по проводящей среде идет ток. Проводимость между электродами равна
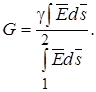
C другой стороны в электростатическом поле с электродами такой же конфигурации емкость между двумя частями электродов, на которых расположены одинаковые по величине и противоположные по знаку заряды Q равна:
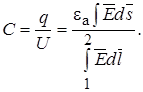
Учтено, что
Если разделить (16.14) на (16.13), то можно получить:

Выражение (16.15) позволяет по известному выражению емкости между какими-либо телами получить выражение для проводимости и наоборот.
Так, например, емкость двухпроводной линии:

где: l – длина проводов, d – расстояние между осями, r – радиус провода.
Чтобы получить выражение для проводимости между двумя параллельными проводами, погруженными в среду с проводимостью g, надо в (16.15) заменить ea на g:
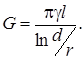
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Электростатическое поле и электрическое поле разница
В XIX веке английский учёный Майкл Фарадей выдвинул гипотезу, что электрическое и магнитное взаимодействия осуществляются посредством особой среды между ними, поля. Любой заряд `q` изменяет свойства пространства вокруг себя – создаёт вокруг себя поле, а уже это поле действует на другие заряды. Развитие науки и техники показало чрезвычайную плодотворность концепции поля. Вся теория электромагнитных явлений со всеми её приложениями существенным образом основывается на концепции поля. По мнению Эйнштейна, идея поля была самым важным открытием со времён Ньютона.
Идея электрического поля большинству людей кажется некоей абстрактной теоретической концепцией, поскольку электрическое поле (в отличие от поля магнитов) в обыденной жизни, в быту невозможно «почувствовать рукой». К вопросу о том, почему это так, мы вернёмся позже. Пока же обратимся к количественному описанию электростатического поля.
Если в поле точечного заряда `q` поместить на расстоянии `r` пробный точечный заряд `q_1`, то на этот заряд будет действовать сила `|vecF_1|=1/(4pi epsilon_0) (|q||q_1|)/(r^2)`. Если в ту же точку поместить другой пробный заряд `q_2`, то на него заряд со стороны заряда `q` будет действовать другая сила `|vecF_2|=1/(4pi epsilon_0) (|q||q_2|)/(r^2)`. Существенно, однако, что отношение силы, действующей на пробный заряд, к его заряду, `(vecF_1)/(q_1)=(vecF_2)/(q_2)`, останется одним и тем же и будет характеристикой не пробных зарядов, но исходного заряда `q` и местоположения `vecr` точки `A`, в которую мы помещали пробные заряды (см. рис. 1). Эта характеристика называется напряжённостью электрического поля точечного заряда `q` в точке `A`. Напряжённость поля есть векторная величина. Её модуль равен
`|vecE|=1/(4pi epsilon_0) (|q|)/(r^2)`. (1.3.1)
Если заряд `q` положительный, то вектор `vecE` в точке `A` направлен в сторону от заряда вдоль прямой, соединяющей точечный заряд `q` и точку `A`; если же заряд `q` отрицательный, то вектор `vecE` в точке `A` направлен в сторону к заряду вдоль той же прямой.
`vecE=1/(4pi epsilon_0) q/(r^2) vece`. (1.3.1′)
Формулу (1.3.1.) иногда записывают в виде `|vecE|=1/(4pi epsilon_0) (|q|*(+1))/(r^2)`; при этом о напряжённости говорят как о силе, действующей со стороны заряда `q` на некий условный единичный положительный точечный заряд `(+1)` (не заряд в `+1` Кл!). Нужно, впрочем, помнить, что сила и напряжённость электрического поля имеют разную размерность. В системе СИ напряжённость электрического поля измеряется в вольтах на метр (В/м): `1`В/м `=1`Н/`1`Кл.
Принцип суперпозиции. Напряжённость есть векторная величина. Это означает, что если имеются два заряда `q_1` и `q_2` каждый из них в некоторой точке создаёт свои напряжённости поля `vecE_1` и `vecE_2`, то результирующая напряжённость (результирующая сила, действующая на единичный положительный заряд, со стороны обоих зарядов) будет равна векторной сумме
получаемой по правилу параллелограмма (рис. 2) или треугольника.
Аналогично, в случае `N` зарядов:
`vecE=vecE_1+vecE_2+. +vecE_N=sum_(k=1)^N vecE_k`, (1.3.3)
причём векторная сумма вычисляется по правилу многоугольника (либо последовательно несколько раз по правилу параллелограмма).
Введя понятие напряжённости электрического поля, мы каждой точке пространства около заряда `q` (или около системы зарядов) приписываем некоторый вектор `vecE=1/(4pi epsilon_0) q/(r^2)vece` (в случае системы зарядов нужно ещё вычислить сумму (1.3.3.)), который, в конце концов, позволяет вычислять по формуле `vecF=q^’vecE` силу, действующую на любой другой заряд `q^’`.
Расстояние между точечными зарядами `q_1=+1` нКл и `q_2=-2` нКл равно `d=13` см. Определить напряжённость результирующего электрического поля обоих зарядов в точке, расположенной на расстоянии `r_1=5` см от первого и `r_2=12` см от второго заряда.
Легко заметить, что `r_1^2+r_2^2=d^2`, т. е. треугольник, образованный зарядами и интересующей нас точкой, прямоугольный. Поэтому напряжённости, создаваемые в этой точке отдельными зарядами, перпендикулярны друг другу (рис. 3). Далее, по теореме Пифагора
`E=sqrt(E_1^2+E_2^2)`, где `E_1=1/(4pi epsilon_0) (q_1)/(r_1^2)=3600` В/м и `E_2=1/(4pi epsilon_0) (|q_2|)/(r_2^2)=1250` В/м.
Электрическое поле равномерно заряженной сферы. Вне равномерно заряженной сферы электрическое поле точно такое же, какое создавал бы помещённый в центр сферы точечный заряд, равный по величине суммарному заряду сферы (рис. 4, а – б). Нетривиальный факт состоит в том, что внутри равномерно заряженной сферы напряжённость электрического поля равна нулю (см. `[2 – 3]`).
Если имеются две концентрические равномерно заряженные сферы, то за пределами обеих сфер поле такое же, какое создавали бы два точечных заряда, равные зарядам сфер и помещённые в их общий центр. В области между сферами внешняя сфера не вносит вклада в напряжённость поля.
Вне равномерно заряженного по объёму шара электрическое поле точно такое же, какое создавал бы помещённый в центр шара точечный заряд, равный по величине суммарному заряду шара. Последнее легко понять: поле шара можно представить как результирующее поле множества тонких шаровых слоёв («сфер»). О том, каким будет поле внутри шара, см. Пример 8.
Оценить заряд Земли `Q`, если известно, что в среднем вблизи поверхности Земли существует статическое электрическое поле, направленное вниз перпендикулярно поверхности Земли в каждой её точке, напряжённость которого равна `E
130` В/м. Радиус Земли `R
Напряжённость электрического поля направлена вниз перпендикулярно поверхности Земли, т. е., к центру Земли. Отсюда можно сделать вывод, что заряд Земли отрицателен. По формуле (1.3.1).
Хотя атмосфера Земли обладает положительным электрическим зарядом, она не вносит вклада в напряжённость электрического поля на поверхности Земли (каждый из её сферических слоёв даёт нулевой вклад в напряжённость поля). Напряжённость поля порядка `130` В/м есть среднее поле вблизи поверхности Земли. При приближении, например, грозовой тучи поле может возрасти в тысячи раз.
Какой максимальный заряд можно сообщить металлическому шарику радиусом `r=1` см, чтобы ещё не происходило пробоя воздуха. Пробойное поле сухого воздуха `E_»пр»
3*10^6` В/м. (Если напряжённость электрического поля больше этого значения, происходит пробой воздуха – воздух начинает проводить электричество (возникает электрический ток) – и заряд стекает с заряженных тел на другие тела.)
По формуле (1.3.1) получаем `q_(max)=4pi epsilon_0E_»пр»r^2
Оценить силу взаимодействия двух шариков радиусом `r=1` см, заряженных до максимально возможного заряда (чтобы ещё не происходило пробоя воздуха вблизи шариков) при расстоянии между центрами шариков `d=10` см. Пробойное поле сухого воздуха `E_»пр»
`f=1/(4pi epsilon_0) (q_(max)^2)/(d^2)=1/(4pi epsilon_0) ((4pi epsilon_0E_»пр»r^2)^2)/(d^2)=(4pi epsilon_0E_»пр»^2r^4)/(d^2)
Мы получили весьма малую силу (сила тяжести, действующая на льдинку массой `1` г объёмом примерно в `1 «см»^3`, почти в `10` раз больше). Вот почему, хотя электрические силы обычно считаются большими, заметить их не всегда легко. Реально мы видим лишь электрическое притяжение друг к другу очень лёгких тел (например, листочков бумаги к наэлектризованной расчёске).
Пользуясь тем свойством, что внутри равномерно заряженной сферы напряжённость электрического поля равна нулю, найти напряжённость поля внутри равномерно по объёму заряженного шара радиусом `R` и зарядом `Q`. (К таким практически равномерно по объёму заряженным шарам можно с хорошей точностью отнести, например, атомные ядра.)
Электрический диполь. Так называется система, состоящая из двух точечных зарядов равных по величине, но противоположных по знаку. Пусть заряды `q_1=-q` и `q_2=+q` в некоторой системе координат характеризуются радиус-векторами `vecr_1` и `vecr_2` (см. рис. 6). Дипольным моментом диполя называется векторная величина `vecp=q_1vecr_1+q_2vecr_2=q(vecr_2-vecr_1)=qvecl`, а величина `l=|vecl|=|vecr_2-vecr_1|` называется плечом диполя.
e/(4pi epsilon_0) (2Rl)/(R^4) =1/(4pi epsilon_0) (2el)/(R^3)=1/(4pi epsilon_0) (2p)/(R^3)
Рассмотрим более сложный пример использования принципа суперпозиции.
По тонкому кольцу радиусом `r` равномерно распределён заряд `q`. Найти напряжённость электрического поля на оси кольца в точке `A`, расположенной на расстоянии `R` от центра (рис. 7).
1/(4pi epsilon_0) q/(R^2)` для точечного заряда.
Электрическое поле бесконечной равномерно заряженной плоскости
Вычисление поля в данном случае требует привлечения знаний высшей математики. Без сложных вычислений можно, однако, сделать два следующих утверждения, основываясь лишь на соображениях симметрии, а также на том факте, что густота линий напряжённости пропорциональна величине `vecE` (см. Учебник):
1) Электрическое поле бесконечной равномерно заряженной плоскости перпендикулярно плоскости (рис. 8). Дело в том, что перпендикуляр к плоскости – единственное выделенное направление в задаче. Если бы вектор `vecE` был направлен под некоторым углом `alpha` к плоскости, мы бы ещё спросили себя: «Чем это направление лучше, чем все другие прямые, имеющие тот же угол `alpha` с плоскостью, и направленные вдоль образующих конуса с углом `alpha` при вершине?» Ясно, что ничем не лучше: если плоскость бесконечная и заряжена одинаково во всех точках, то и любые направления вдоль неё эквивалентны друг другу.
Величина вектора напряжённости `vecE` может быть вычислена по формуле
Хотя в природе не существует бесконечных равномерно заряженных плоскостей, формула (1.3.4) с успехом используется для расчётов электрических полей заряженных тел в виде больших пластин или просто плоских объектов при небольшом удалении от центральной их части.
Электростатическое поле создаётся двумя бесконечными параллельными плоскостями, заряженными с поверхностными плотностями заряда `sigma_1=-1 «нКл»//»м»^2` и `sigma_2=+1 «нКл»//»м»^2`. Определить напряжённость электрического поля между плоскостями и снаружи.
`|sigma_1|=sigma_2-=sigma`, `|E_1|=|E_2|-=E=sigma//2 epsilon_0`. Далее воспользуемся принципом суперпозиции полей. Между плоскостями напряжённости полей отдельных пластин направлены в одну и ту же сторону (рис. 9), по этому результирующая напряжённость `E_(«in»)=2E=sigma//epsilon_0=113` В/м и направлена от положительной плоскости к отрицательной. Снаружи поля разных плоскостей направлены в противоположные стороны, поэтому результирующая напряжённость поля там `E_(ex)=0`.
Пользуясь принципом суперпозиции, доказать, что напряжённость электрического поля равномерно заряженной полусферической чаши во всех точках плоскости, стягивающей края чаши (как кожа на барабане), перпендикулярна этой плоскости.
Мысленно дополним полусферу ещё одной такой же полусферой так, чтобы получилась целая сфера. Напряжённость поля внутри равномерно заряженной сферы равна нулю. С другой стороны, эта напряжённость складывается из двух напряжённостей – исходной полусферы `vecE` и мысленно добавленной `vecE^’`. Таким образом, имеем равенство `vecE+vecE^’=0`, или `vecE=-vecE^’`. Последнее возможно только в том случае, если углы наклона векторов `vecE` и `vecE^’` к плоскости одинаковы, т. е. равны `90^@` (рис. 10).