Ряд фибоначчи что это простыми словами
Последовательность Фибоначчи: что это такое простыми словами, где применяется и как определяется
Человечество на протяжении многих тысяч лет сталкивалось с различными закономерностями в окружающем их мире. По мере развития науки люди начали описывать многие вещи с помощью математических инструментов. Создание моделей позволяет понять суть различных процессов, а также создает возможность прогнозирования. Один из таких способов – последовательность Фибоначчи.
Как Леонардо Фибоначчи изобрел свою известную последовательность
Леонардо Пизано по прозвищу Фибоначчи – европейский математик 12 в. Родом из Пизы, он по воле отца направился для изучения математики и торгового дела в Алжир к арабским учителям.
Фибоначчи открыл свою известную последовательность, когда задался вопросом о разведении кроликов. Суть задачи: «Пару кроликов заселяют на поляну. Сколько пар будет жить на этом месте через год?». Для решения были введены упрощения: кролики в течение года не умирают, половой зрелости достигают спустя месяц после рождения, потомки появляются только спустя месяц после зачатия.
Таким образом, в этой задаче последовательность определяется так:
В конце года на поляне будет 144+233=377 пар кроликов.
Что это и для чего нужно
Последовательность Фибоначчи простыми словами – это прогрессия, состоящая из целых чисел, следующих друг за другом с определенной закономерностью. Каждый последующий элемент равен сумме двух предыдущих.
Большой интерес представляет частное двух соседних чисел, для всех элементов ряда приблизительно равное цифре 1,618. Это значение получило название «золотое сечение». Именно оно лежит в основе натуральной гармонии нашей Вселенной, присущей галактикам, цветам, животным.
Последовательность чисел Фибоначчи
Так исторически сложилось, что первыми выявили и описали «золотое сечение» древнегреческие математики. Оно представляло собой деление отрезка АВ точкой С на части таким образом, что большая часть отрезка относится к меньшей, как весь отрезок к большей части: ВС/АС=АВ/ВС.
Позднее, в начале 13-го века, Фибоначчи привел обоснование и доказательства существования этой последовательности и «золотого сечения». В 19 веке теоретик Эдуард Люка дал название этой прогрессии — «последовательность Фибоначчи».
Где используют
Золотое сечение наряду с загадочными свойствами чисел Фибоначчи с далеких времен и по сей день привлекают внимание ученых. Область применения последовательности довольна широка. Это может быть искусство, архитектура. Например, правило встречается на полотне И. Левитана «Сумерки. Луна» с выстроенным центром (Луной), линией горизонта, темными акцентами по правилам золотого сечения в соотношении 1,618. Соответственно, здесь и будут расположены наиболее важные части экспозиции.
В архитектуре пример «золотых» линий — знаменитая пирамида Хеопса. В древнегреческих строениях универсальное правило можно проследить, изучая Парфенон. В те времена считалось, что объекты с именно таким соотношением частей наиболее приятны для глаз человека.
Применение в трейдинге
Первым человеком, кто решил заняться изучением рынков на основе применения последовательности чисел Фибоначчи, является Ральф Нельсон Эллиот. Будучи финансистом, он смог обнаружить и определенную закономерность в поведении фондовых рынков, также поддающихся правилу золотого сечения.
Применение последовательности Фибоначчи в трейдинге
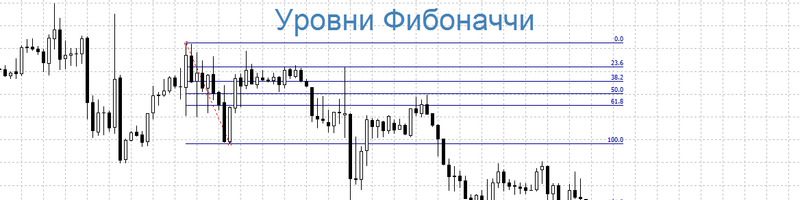
Коррекции Фибоначчи
Коррекции, или уровни Фибоначчи – это инструмент технического анализа, служащий для прогнозирования уровней поддержки и сопротивления.
Для построения требуется произвести следующий порядок действий:
Значения коэффициентов получают по следующей формуле, согласно числам Фибоначчи (0,1,1,2,3,5,8,13,21,34,55,89,144…):
Существуют еще 3 уровня, не входящих в соотношения Фибоначчи:
Дуги Фибоначчи
Один из индикаторов, представляющий дуги, которые могут быть уровнями поддержки и сопротивления. Трейдеры при помощи этого инструмента имеют возможность прогнозировать моменты разворота рынка, чтоб своевременно зафиксировать прибыль.
Построение производят также на основе экстремумов графика. Определяют желаемую точку. Затем от нее на расстояниях 38,2%, 50% и 61,8% отстраивают дуги.
Тем самым можно определить уровни сопротивления и поддержки цены.
При растущем тренде с помощью дуг возможно понять, до какого значения опустится цена перед ее следующим подъемом. И, наоборот, при снижении цены акции дуги показывают, как может вырасти цена до ее следующего падения.
Веера Фибоначчи
Представляют диагональные линии, исходящие из одной точки. Формой походят на веер.
Для построения требуется произвести следующие действия;
Временные зоны Фибоначчи
Это инструмент технического анализа рынка, который представляет ряд вертикальных линий, построенных в рамках числовых значений Фибоначчи. Принцип работы основан на временных отрезках, а не на движении цен.
На графике отмечают явный ценовой тренд, основанный на точках экстремума. Горизонтальное расстояние между ними – единичный отрезок. Далее строят параллельные вертикальные линии. Эти прямые будут характеризовать временные зоны, в которых с некоторой долей вероятности можно ожидать падение или взлета цен. Первый уровень должен совпадать с пиковым значением тренда на графике. Но для большей уверенности желательно, чтоб и второй уровень приходился на экстремальное значение.
Золотое сечение и числа Фибоначчи
Человек стремится к знаниям, пытается изучить мир, который его окружает. В процессе наблюдений появляются многочисленные вопросы, на которые, соответственно, требуется найти ответы. Человек ищет эти ответы, а находя их, появляются другие вопросы.
Оказывается, закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это можно объяснить последовательностью Фибоначчи.
Леонардо был рожден в Пизе. Впоследствии получил прозвище Фибоначчи, что означает «хорошо рожденный сын». Когда Леонардо жил со своим отцом в странах Северной Африки, он изучал математику с арабскими учителями. Получив весь необходимый материал, он создал собственную книгу – «Книгу абака». Именно этот человек становится первым средневековым учёным, познакомившим Европу с арабской системой счисления, которой мы пользуемся всю нашу жизнь[1].
Основная задача, поясняющая возникновение ряда чисел Фибоначчи – задача о кроликах. Вопрос задачи звучит так: «Сколько пар кроликов в один год рождается от одной пары?». К задаче дано пояснение, что пара через месяц рождает ещё одну пару, а по природе кролики начинают объектом рождать потомство на второй месяц после своего рождения. Автор даёт нам решение задачи. Получается, что в первый месяц первая пара родит ещё одну. Во второй месяц первая пара родит ещё одну – будет три пары. В третий месяц родят две пары — изначально данная и рождённая в первый месяц. Получается пять пар. И так далее. Используя такую же логику в рассуждении, мы получим, что в четвёртый месяц будет 8 пар, в пятый– 13, в шестой – 21, в седьмой 34, в восьмой — 55, в девятый — 89, в десятый 144, в одиннадцатый – 233, в двенадцатый — 377[2](рис. 1).
Из этой задачи и можно вывести саму последовательность чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,… В основе этой последовательности лежит алгоритм: начиная с «1, 1» следующим числом будет сумма двух предыдущих чисел. Разделив любой член данной последовательности на член, который стоит перед ним, мы получим величину, называемую «пропорцией Золотого сечения» — примерно 1, 618[3].
В эпоху Возрождения художники открыли некие зрительные центры, которые, влияя на психику человека, невольно приковывают наше внимание. Данные точки не зависят от формата картины. Их всего четыре, они делят картину в пропорциях Золотого сечения- примерно 3/8 и 5/8 (рис.2).
Для того чтобы привлечь внимание зрителя к определенному элементу картины, необходимо совместить его с одним из зрительных центров. Данное открытие назвали «золотое сечение картины»[4].
Правило золотого сечения используется в стоматологии, именно они используются при художественной реставрации зубов, их восстановлении. Рассмотрим эстетическое восстановление передних зубов, фронтального зубного ряда (рис. 3)[5].
Золотые пропорции включают в себя такие моменты:
— как ширина верхнего переднего зуба относится к ширине нижнего;
— как соотносятся между собой по ширине:
2 резца в нижнем фронтальном ряду;
двое резцов в верхнем ряду;
— какое имеется расстояние между премолярами и т.д.
Так же правило золотого сечения используется в косметологии и пластической хирургии. У людей с красивыми лицами существует идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это явление называется «динамической симметрией» или «динамическим равновесием».
Расстояние от линии смыкания губ до крыльев носа пропорционально расстоянию от линии губ до низшей точки подбородка в соотношении 1: 1,618. Ещё существует множество соотношений на лице, которые представлены на рисунке 4[6].
Числа Фибоначчи и Золотое сечение чтобы также используется и в психологии. Например, чтобы выяснить, как развивается механизм творчества, В.В. Клименко воспользовался математикой, а именно законами чисел Фибоначчи и пропорцией «золотого сечения» — законами природы и жизни человека. Если развернуть в ряд числа Фибоначчи, то получим: 1,1, 2, 3, 5, 8, 13, 21, 34, 55, 89 и т.д. Отношение между числами Фибоначчи составляет 0,618. Развитие человека также происходит соответственно данной пропорции и подчиняется закону ее чисел, разделяя нашу жизнь на этапы с теми или иными доминантами механизма творчества [7].
Числа Фибоначчи делят нашу жизнь на этапы по количеству прожитых лет:
• 0 —начало отсчета — ребёнок родился. У него еще отсутствуют не только психомоторика, мышление, чувства, воображение, но и оперативный энергопотенциал. Он — начало новой жизни, новой гармонии;
• 1 — ребенок овладел ходьбой и осваивает ближайшее окружение;
• 2 — понимает речь и действует, пользуясь словесными указаниями;
• 3 — действует посредством слова, задаёт вопросы;
• 5 — «возраст грации» — гармония психомоторики, памяти, воображения и чувств, которые уже позволяют ребёнку охватить мир во всей его целостности;
• 8 — на передний план выходят чувства. Им служит воображение, а мышление силами своей критичности направлено на поддержку внутренней и внешней гармонии…
Закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это можно объяснить последовательностью Фибоначчи.
В заключении отмечу, что данная работа является законченным исследованием и при этом имеет ряд перспектив. В дальнейшем возможно исследовать как числа Фибоначчи используются в биологии, химии, как это можно использовать и применять на практике в бытовых условиях.
1. Воробьев Н.Н. Числа Фибоначчи. – 5-е изд. – М.: Наука, 1978 – 144с.
Число Фибоначчи. Почему оно так популярно в природе?
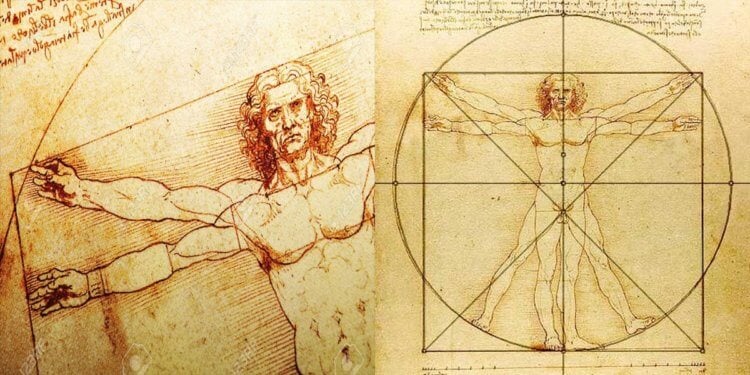
Таинственное число Фибоначчи, равное 1,618, будоражит умы ученых уже на протяжении нескольких тысячелетий. Кто-то считает это число строителем мироздания, кто-то называет его числом Бога, а кто-то, не мудрствуя лукаво, просто применяет его на практике и получает невероятные архитектурные, художественные и математические творения. Число Фибоначчи было обнаружено даже в пропорциях знаменитого «Витрувианского человека» Леонардо Да Винчи, который утверждал, что знаменитое число, пришедшее из математики, руководит всей Вселенной.
«Витрувианский человек» Леонардо да Винчи обладает идеальными пропорциями, основанными на знании свойств числа Фибоначчи
Кто такой Фибоначчи?
Леонардо Пизанский считается самым первым крупным математиком в истории средневековой Европы. Несмотря на это, свое знаменитое прозвище «Фибоначчи» ученый получил далеко не из-за своих экстраординарных математических способностей, но из-за своего везения, так как «боначчи» по-итальянски означает «удачливый». Перед тем как стать одним из самых известных математиков раннего Средневековья, Леонардо Пизанский изучал точные науки у самых продвинутых учителей своего времени, которыми считались арабы. Именно благодаря этой деятельности Фибоначчи, в Европе появились десятичная система счисления и арабские цифры, которыми мы пользуемся до сих пор.
В одном из своих самых известных трудов под названием «Liber abaci», Леонардо Пизанский приводит уникальную закономерность чисел, которые при постановке в ряд образуют линию цифр, каждая из которых является суммой двух предыдущих чисел.
Последовательность Фибоначчи
Иными словами, последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее.
Каждое число из ряда Фибоначчи, разделенное на последующее, имеет значение, стремящееся к уникальному показателю, которое составляет 1,618. Первые числа ряда Фибоначчи не дают настолько точное значение, однако по мере нарастания, соотношение постепенно выравнивается и становится все более точным.
Леонардо Пизанский — тот самый создатель числа Фибоначчи
Где используется число Фибоначчи
Из-за своего повсеместного применения в природе, золотое сечение (именно так число Фибоначчи иногда называют в искусстве и математике) считается одним из самых гармонизирующих законов мироздания, который упорядочивает структуру окружающего нас мира и направляет жизнь на развитие. Так, правило золотого сечения применяется природой для образования траекторий движения вихревых потоков в ураганах, при образовании эллиптических галактик, к которым относится и наш Млечный Путь, при «строительстве» раковины улитки или ушной раковины человека, направляет движение косяка рыб и показывает траекторию движения испуганной стаи оленей, врассыпную убегающую от хищника.
Проявление золотого сечения в природе
Эстетичность такой гармонизации мироздания воспринимается человеком, который всегда стремился улучшить окружающую его действительность, в качестве стабилизирующего природу закона. Находя золотое сечение в лице того или иного человека, мы инстинктивно воспринимаем собеседника в качестве гармоничной личности, чье развитие происходит без сбоев и нарушений. Этим можно объяснить то, почему иногда нам по непонятным причинам больше нравится одно лицо, чем другое. Оказывается, о наших возможных симпатиях позаботилась природа!
Как вы считаете, является ли повсеместное применение числа Фибоначчи в природе совпадением или свидетельством наличия некоего вселенского разума? Давайте попробуем обсудить этот вопрос в нашем Telegram-чате.
Наиболее распространенное определение золотого сечения гласит, что меньшая часть так относится к большей, как большая часть относится ко всему целому. Уникальное правило встречается во всех областях природы, науки и искусства, позволив некоторым именитым исследователям Средних Веков сделать предположение, что три основные части золотого сечения олицетворяют собой христианских Отца, Сына и Святого Духа.
Правилу золотого сечения следуют даже галактики. Наш Млечный Путь в этом плане не является исключением
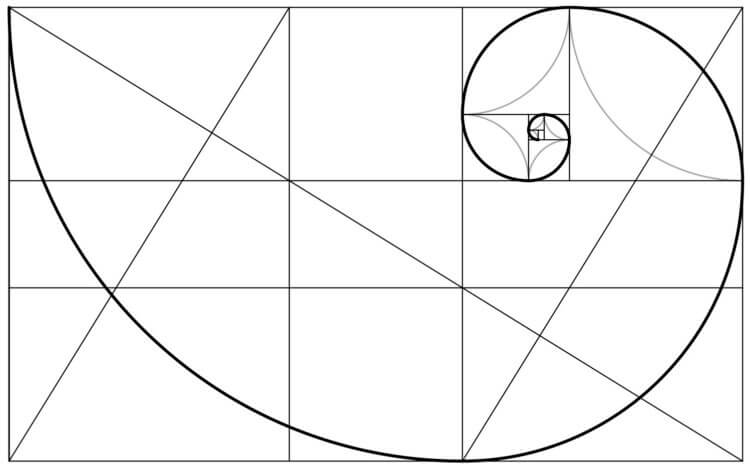
Что такое золотое сечение
С точки зрения математики, золотое сечение представляет собой некую идеальную пропорцию, к которой каким-то образом стремится все живое и неживое в природе.
Так выглядит «золотое сечение»
Используя основные принципы ряда Фибоначчи, растут семечки в центре подсолнуха, движется спираль ДНК, был построен Парфенон и написана самая знаменитая картина в мире — «Джоконда» Леонардо Да Винчи.
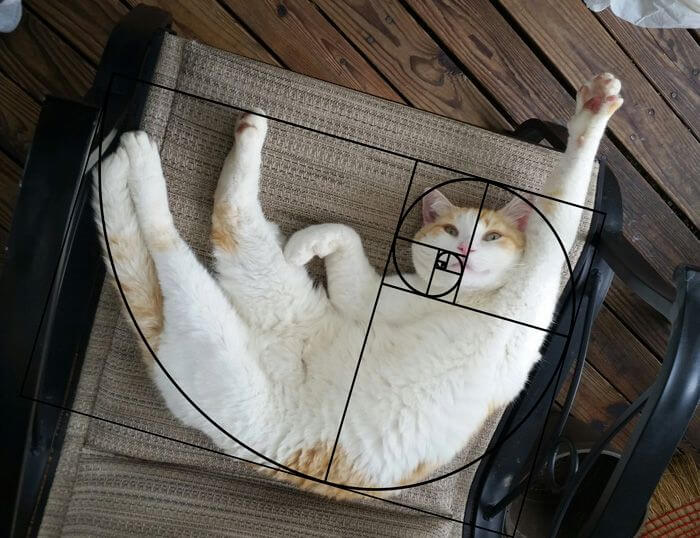
Даже коты неосознанно (хотя, кто знает?) следуют принципу золотого сечения, становясь любимцами большей части населения планеты
Есть ли в природе гармония? Несомненно, есть. А ее доказательством служит число Фибоначчи, происхождение которого нам еще только предстоит отыскать.
Новости, статьи и анонсы публикаций
Свободное общение и обсуждение материалов
Еще несколько тысяч лет назад Платон предположил: то, что мы видим, может быть вовсе не реальным. С появлением компьютеров идея обрела новую жизнь, особенно …
Когда-то давно на нашей планете существовало несколько сотен видов нелетающих птиц, но сегодня их осталось только около 60 видов. 🐦 Это связано с тем, что эти создания долгое время жили в местах без хищников и внезапно появившиеся люди начали их истреблять. Но что еще известно ученым?
В ходе изучения спутниковых снимков ученые выяснили, из поверхности антарктического ледника Эймери пропало огромное озеро талой воды. 🧊 Давайте выясним, куда оно могло исчезнуть?